KDtree浅谈

KDtree浅谈

1.对KDtree的理解

　　首先要知道$KDtree$的用处，$KDtree$是用来进行多维数点的，一般这些点都是在在而二维及二维以上，因为一维上的问题，我们基本都可以运用线段树来解决。我对$KDtree$的理解就是一个自带剪枝的暴力，并且这个剪枝因为我们对这些多维上的点的较优秀的排列而显得十分有用。

2.前置知识

　　在学习$KDtree$之前要先知道并会运用西面三个知识点：

​　　1) 首先，要会建二叉搜索树，因为整个$KDtree$就是一颗二叉搜索树。

　　2) 还需要知道什么事估价函数，因为剪枝的时候要运用到估价函数。

​　　3) 对空间的想象能力，因为$KDtree$是处理图形上的问题，所以还需要有一定的空间想象能力。

3.KDTree的讲解

　　因为$KDtree$是一种优美的暴力，并且我们要在上面剪枝，所以我们自然想让每一次剪枝，剪下去尽可能大的部分，所以我们能想到每一次将区间等大的分割，既然要的等大的分割，又要是二叉搜索树，我们就要让中间值作为当前节点，所有比它小的都放在它的左面，比它大的都放在它的右面。

　　知道大致思路了，就要来定义什么是大小了，因为一个点是在多维里，所以和它有关的值有多个。最好想的就是按读入的顺序，进行排序，第一维作为第一关键字，第二维作为第二关键字，以此类推。我们根据这些点的维度将它们从小到大排序（下面已二维上的点为例），每一次取当前区间的中间值来建树。这样我们就能将整个图分成下面的形式：

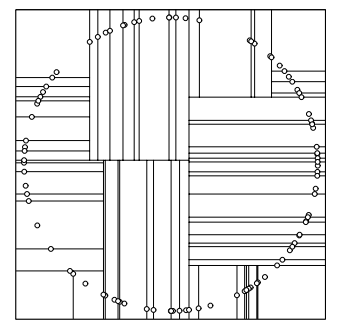
　　显然这种分法分出的图并不是最有利，因为每一点的管辖范围都太小了。我们考虑另一种分割方式，我们将这些点的排序方式进行改变，我们将排序的关键字每一次向顺时针进行转动，即我们第一次排序的第一关键字是第一维，第二次是第二维……第$n$次是第$n\%维数+1$维。这样上面的图形就可以改变成为：

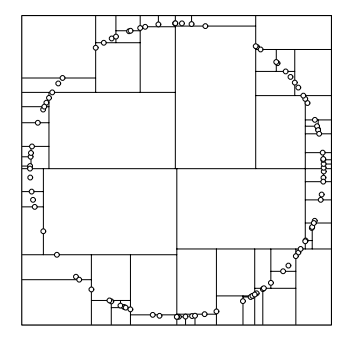
　　这样我们在剪枝的时候就能剪去更多的节点。

　　知道了如何去排序，我们现在就要知道怎么来找中间值。在函数库里面有一个函数$nth\_element$，这个就能实现我们要的功能。这个函数不知道实现的话，可以上网上找一下学习一下。我们在建树的时候要维护出来几个值，这几个值的运用在下面会进行讲解。这几个值是$mn[0]，mx[0]，mn[1]，mx[1]$，分别表示以当前节点为根的子树第一维的最小值和最大值，第二维的最小值和最大值，这样我们在建树的时候应该更新。

struct Node {long long pla[2],mn[2],mx[2];int id,lson,rson;}node[N];
bool cmp(const Node &a,const Node &b) {return a.pla[sta]<b.pla[sta];}
void up(int p,int k)
{
	node[p].mn[0]=min(node[p].mn[0],node[k].mn[0]);
	node[p].mx[0]=max(node[p].mx[0],node[k].mx[0]);
	node[p].mn[1]=min(node[p].mn[1],node[k].mn[1]);
	node[p].mx[1]=max(node[p].mx[1],node[k].mx[1]);
}
int build(int l,int r,int now)
{
	sta=now;int mid=(l+r)>>1;
	nth_element(node+l,node+mid,node+r+1,cmp);
	node[mid].mn[0]=node[mid].mx[0]=node[mid].pla[0];
	node[mid].mn[1]=node[mid].mx[1]=node[mid].pla[1];
	if(l!=mid) node[mid].lson=build(l,mid-1,(now+1)%2);
	if(r!=mid) node[mid].rson=build(mid+1,r,(now+1)%2);
	if(node[mid].lson) up(mid,node[mid].lson);
	if(node[mid].rson) up(mid,node[mid].rson);
	return mid;
}

　　建树之后，我们就可以在里面进行一些操作，比如找离定点的最远点，最近点，维护矩形内信息等等，下面就是一些估价函数的代码，以及矩形内区间赋值。

　　找离当前点的最近点的估价函数及查询（欧几里得距离）：

long long dis(int p) {return squ(node[p].pla[0]-x)+squ(node[p].pla[1]-y);}
long long getdis(int p)
{
	long long tmp=0;
	tmp+=squ(max(abs(node[p].mx[0]-x),abs(node[p].mn[0]-x)));
	tmp+=squ(max(abs(node[p].mx[1]-y),abs(node[p].mn[1]-y)));
	return tmp;
}
void ask(int p)
{
	long long tmp=dis(p);tmpx.dis=tmp,tmpx.id=node[p].id;
	if(q.top().dis<=tmpx.dis) q.push(tmpx),q.pop();
	long long tmpl=(node[p].lson)?getdis(node[p].lson):-inf;
	long long tmpr=(node[p].rson)?getdis(node[p].rson):-inf;
	if(tmpl>tmpr)
	{
		if(tmpl>=q.top().dis&&node[p].lson) ask(node[p].lson);
		if(tmpr>=q.top().dis&&node[p].rson) ask(node[p].rson);
	}
	else
	{
		if(tmpr>=q.top().dis&&node[p].rson) ask(node[p].rson);
		if(tmpl>=q.top().dis&&node[p].lson) ask(node[p].lson);
	}
}

　　找离当前点的最远点的估价函数及查询（曼哈顿距离）：

int getdis_mx(int p)
{
    int tmp=0;
    tmp+=max(abs(node[p].mx[0]-x),abs(node[p].mn[0]-x));
    tmp+=max(abs(node[p].mx[1]-y),abs(node[p].mn[1]-y));
    return tmp;
}
void ask_mx(int p)
{
    int tmp=abs(node[p].pla[0]-x)+abs(node[p].pla[1]-y);
    if(tmp>lenth_mx) lenth_mx=tmp;
    int tmpl=(node[p].lson)?(getdis_mx(node[p].lson)):-inf;
    int tmpr=(node[p].rson)?(getdis_mx(node[p].rson)):-inf;
    if(tmpl>tmpr)
    {
        if(tmpl>lenth_mx) ask_mx(node[p].lson);
        if(tmpr>lenth_mx) ask_mx(node[p].rson);
    }
    else
    {
        if(tmpr>lenth_mx) ask_mx(node[p].rson);
        if(tmpl>lenth_mx) ask_mx(node[p].lson);
    }
}

　　找离当前点的最远点的估价函数及查询（曼哈顿距离）：

int getdis_mn(int p)
{
    int tmp=0;
    if(x<node[p].mn[0]) tmp+=node[p].mn[0]-x;
    if(x>node[p].mx[0]) tmp+=x-node[p].mx[0];
    if(y<node[p].mn[1]) tmp+=node[p].mn[1]-y;
    if(y>node[p].mx[1]) tmp+=y-node[p].mx[1];
    return tmp;
}
void ask_mn(int p)
{
    int tmp=abs(node[p].pla[0]-x)+abs(node[p].pla[1]-y);
    if(tmp&&tmp<lenth_mn) lenth_mn=tmp;
    int tmpl=(node[p].lson)?(getdis_mn(node[p].lson)):inf;
    int tmpr=(node[p].rson)?(getdis_mn(node[p].rson)):inf;
    if(tmpl<tmpr)
    {
        if(tmpl<lenth_mn) ask_mn(node[p].lson);
        if(tmpr<lenth_mn) ask_mn(node[p].rson);
    }
    else
    {
        if(tmpr<lenth_mn) ask_mn(node[p].rson);
        if(tmpl<lenth_mn) ask_mn(node[p].lson);
    }
}

　　矩阵赋值，矩阵查找：

void pushdown(int p)
{
    if(!node[p].tag) return;
    if(node[p].lson) node[node[p].lson].tag=node[node[p].lson].col=node[p].tag;
    if(node[p].rson) node[node[p].rson].tag=node[node[p].rson].col=node[p].tag;
    node[p].tag=0;
}
void change(int p,int w,int x,int y,int z,int col)
{
    if(!p) return;
    if(node[p].mx[0]<w||node[p].mn[0]>x) return;
    if(node[p].mx[1]<y||node[p].mn[1]>z) return;
    pushdown(p);
    if(node[p].pla[0]>=w&&node[p].pla[0]<=x&&
        node[p].pla[1]>=y&&node[p].pla[1]<=z) node[p].col=col;
    if(node[p].mn[0]>=w&&node[p].mx[0]<=x&&
        node[p].mn[1]>=y&&node[p].mx[1]<=z) {node[p].tag=node[p].col=col;return;}
    change(node[p].lson,w,x,y,z,col),change(node[p].rson,w,x,y,z,col);
}
int find(int p,int w,int x,int y,int z)
{
    if(!p) return 0;
    if(node[p].mx[0]<w||node[p].mn[0]>x) return 0;
    if(node[p].mx[1]<y||node[p].mn[1]>z) return 0;
    pushdown(p);
    if(node[p].pla[0]==w&&node[p].pla[1]==y) return node[p].col;
    return max(find(node[p].lson,w,x,y,z),find(node[p].rson,w,x,y,z));
}