Codeforces Round #647 (Div. 2) - Thanks, Algo Muse! C. Johnny and Another Rating Drop (规律,二进制)

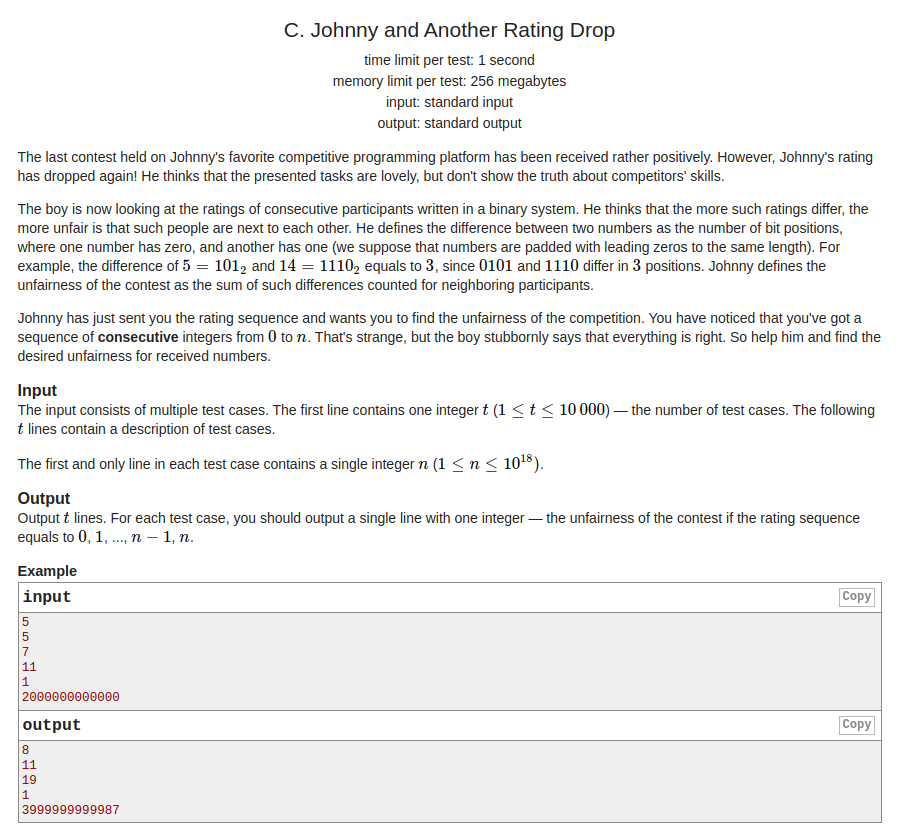
• 题意:有一个正整数\(n\),要求写出所有\(1\)~\(n\)的二进制数,统计相邻的两个二进制同位置上不同数的个数.

• 题解:打表找规律,不难发现:

  ​ \(00000\)

  ​ \(00001\)

  ​ \(00010\)

  ​ \(00011\)

  ​ \(00100\)

  ​ \(00101\)

  ​ 当最低位时,每次都变换,由低位向高位,每\(2*i\)次变换一次,直接位运算暴力即可.

• 代码:

  #include <iostream>
  #include <cstdio>
  #include <cstring>
  #include <cmath>
  #include <algorithm>
  #include <stack>
  #include <queue>
  #include <vector>
  #include <map>
  #include <set>
  #include <unordered_set>
  #include <unordered_map>
  #define ll long long
  #define fi first
  #define se second
  #define pb push_back
  #define me memset
  const int N = 1e6 + 10;
  const int mod = 1e9 + 7;
  const int INF = 0x3f3f3f3f;
  using namespace std;
  typedef pair<int,int> PII;
  typedef pair<ll,ll> PLL;
  
  int t;
  ll n;
  
  int main() {
      ios::sync_with_stdio(false);cin.tie(0);
      cin>>t;
       while(t--){
           cin>>n;
           ll now=n;
           ll ans=0,p=1;
           while(now){
               ans+=n/p;
               p*=2;
               now>>=1;
           }
           printf("%lld\n",ans);
       }
  
      return 0;
  }