C#实现Levenshtein distance最小编辑距离算法

Levenshtein distance，中文名为最小编辑距离，其目的是找出两个字符串之间需要改动多少个字符后变成一致。该算法使用了动态规划的算法策略，该问题具备最优子结构，最小编辑距离包含子最小编辑距离，有下列的公式。

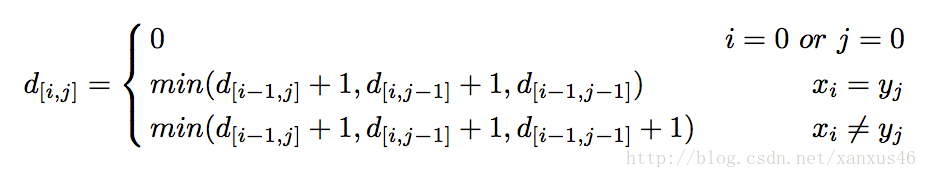
其中d[i-1,j]+1代表字符串s2插入一个字母才与s1相同，d[i,j-1]+1代表字符串s1删除一个字母才与s2相同，然后当xi=yj时，不需要代价，所以和上一步d[i-1,j-1]代价相同，否则+1，接着d[i,j]是以上三者中最小的一项。

算法实现（C#）：

假设两个字符串分别为source，target，其长度分别为columnSize，rowSize，首先申请一个（columnSize+1）*（rowSize+1）大小的矩阵，然后将第一行和第一列初始化，matrix[i,0]=i，matrix[0,j]=j，接着就按照公式求出矩阵中其他元素，结束后，两个字符串之间的编辑距离就是matrix[rowSize, columnSize]的值，代码如下：

    public class StringComparator
    {
        public static int LevenshteinDistance(string source, string target)
        {
            int columnSize = source.Length;
            int rowSize = target.Length;
            if (columnSize == )
            {
                return rowSize;
            }
            if (rowSize == )
            {
                return columnSize;
            }
            int[,] matrix = new int[rowSize + , columnSize + ];
            for (int i = ; i <= columnSize; i++)
            {
                matrix[, i] = i;
            }
            for (int j = ; j <= rowSize; j++)
            {
                matrix[j, ] = j;
            }
            for (int i = ; i < rowSize; i++)
            {
                for (int j = ; j < columnSize; j++)
                {
                    int sign;
                    if (source[j].Equals(target[i]))
                        sign= ;
                    else
                        sign = ;
                    matrix[i + , j + ] = Math.Min(Math.Min(matrix[i, j] +  sign, matrix[i + , j] + 1), matrix[i, j + ] + );
                }
            }

            return matrix[rowSize, columnSize];
        }

        public static float StringSimilarity(string source, string target)
        {
            int distance = LevenshteinDistance(source, target);
            float maxLength = Math.Max(source.Length, target.Length);

            return (maxLength - distance) / maxLength;
        }
    }