kmeans算法思想及其python实现

第十章 利用k-均值聚类算法对未标注的数据进行分组

一．导语

聚类算法可以看做是一种无监督的分类方法，之所以这么说的原因是它和分类方法的结果相同，区别它的类别没有预先的定义。簇识别是聚类算法中经常使用的一个概念，使用这个概念是为了对聚类的结果进行定义。

聚类算法几乎可以用于所有的对象，并且簇内的对象越相似，效果越好。

二．K-均值聚类算法的基本概念

K-均值聚类算法它的目的是将数据分成k个簇。它的一般过程是如下：

随机的选择k个数据点作为初始的质心

当任意一个簇的分配结果发生变化的情况下

对于每一个数据点

对于每一个质心

计算数据点到质心的距离

将当前的数据点分配到距离最近的那个质心所在的簇

对于每一个簇计算其质心

在上面的过程中质心的计算方法一般采用平均；距离的计算方法可以自由选择，比如欧氏距离等等，但是不同的距离度量方式可能会有不同的结果。

K-均值聚类算法它的特点：

1.优点：计算简便，算法简单，容易实现

2.缺点：容易陷入局部最小，对于大数据样本收敛较慢

3.适用的数据类型：数值型数据（如果是标称型数据可以考虑转化成数值型数据）

三．K-means算法的具过程

1.首先从文件中读取数据并保存到数组中。

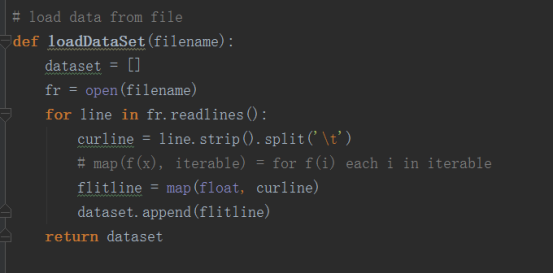
2.定义距离函数

3.初始化质心。在初始化质心时采用的方法是对于每一个特征在它给定的范围之内进行随机

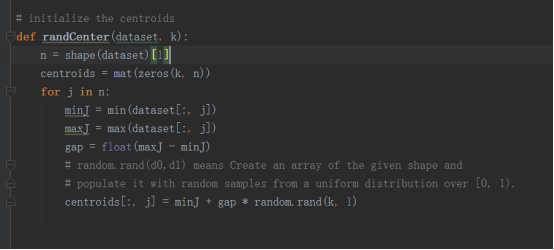
4.kmeans算法的实现

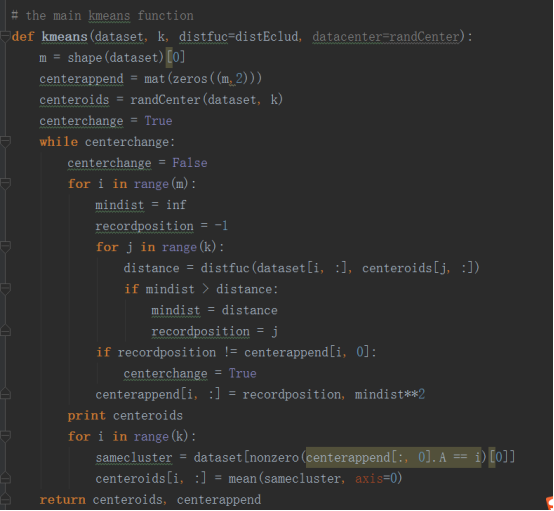
五．使用后处理来提高聚类性能

因为我们使用聚类算法的时候很容易获得局部最小值，而不是全局最小值，所以需要采取一些措施来提高聚类的性能。

当然最简单的就是增加簇的个数，但是这样违背了我们优化的初衷，因此我们采用了后处理的方式进行优化。所谓的后处理指的就是找到簇内误差平方和最大的那个簇，然后将这个簇拆分成两个簇，因为要维持簇的个数不变，我们有需要找到两个出错的质心进行合并。这里衡量质心是否为出错质心有两种量化方法：一是将距离最近的两个质心定义为出错质心；二是将合并后误差平方和增幅最小的两个质心作为出错质心。

六．二分k-均值算法

二分k-均值算法是为了解决聚类算法局部最小的问题而提出的。它的基本思想是首先将所有的点看做是一个簇，然后2-means算法将簇一分为二，然后选择其中一个簇继续划分，选择哪一个簇这决定于对其划分是否能够最大程度的降低误差平方和。一种常见的方法如下：

将所有的点看做是一个簇

当簇的个数小于k时

对于每一个簇

计算当前簇的总误差1

计算将当前簇一分为二后的总误差2

选择总误差1和总误差2差值最大的簇作为下一个划分的簇

（也可以选择划分后簇的总误差最小的簇作为所选择的的划分的簇）

当然还有一种更简单的方式就是直接选择总误差最大的簇作为下一个要划分的簇。

根据上述的算法，我们可以得到如下的代码

def bikmeans(dataSet, k, distMeas=distEclud):
    m = shape(dataSet)[0]
    clusterAssment = mat(zeros((m, 2)))
    centroid0 = mean(dataSet, axis=0).tolist()[0]
    centList = [centroid0]  # create a list with one centroid
    for j in range(m):  # calc initial Error
        clusterAssment[j, 1] = distMeas(mat(centroid0), dataSet[j, :]) ** 2
    while (len(centList) < k):
        lowestSSE = inf
        for i in range(len(centList)):
            ptsInCurrCluster = dataSet[nonzero(clusterAssment[:, 0].A == i)[0],
                               :]  # get the data points currently in cluster i
            centroidMat, splitClustAss = kmeans(ptsInCurrCluster, 2, distMeas)
            sseSplit = sum(splitClustAss[:, 1])  # compare the SSE to the currrent minimum
            sseNotSplit = sum(clusterAssment[nonzero(clusterAssment[:, 0].A != i)[0], 1])
            print "sseSplit, and notSplit: ", sseSplit, sseNotSplit
            if (sseSplit + sseNotSplit) < lowestSSE:
                bestCentToSplit = i
                bestNewCents = centroidMat
                bestClustAss = splitClustAss.copy()
                lowestSSE = sseSplit + sseNotSplit
        bestClustAss[nonzero(bestClustAss[:, 0].A == 1)[0], 0] = len(centList)  # change 1 to 3,4, or whatever
        bestClustAss[nonzero(bestClustAss[:, 0].A == 0)[0], 0] = bestCentToSplit
        print 'the bestCentToSplit is: ', bestCentToSplit
        print 'the len of bestClustAss is: ', len(bestClustAss)
        centList[bestCentToSplit] = bestNewCents[0, :].tolist()[0]  # replace a centroid with two best centroids
        centList.append(bestNewCents[1, :].tolist()[0])
        clusterAssment[nonzero(clusterAssment[:, 0].A == bestCentToSplit)[0],
        :] = bestClustAss  # reassign new clusters, and SSE
    return mat(centList), clusterAssment

七．对地图上的点进行聚类

对地图上的点进行聚类的时候，首先是获取数据和分析数据，这两部省略。假设我们已经拥有了数据，该数据保存在places.txt文件中，并且文件中的第四列和第五列是我们需要的数据。现在我们将根据bikmeans算法找到当前数据中的五个簇,并将结果显示出来

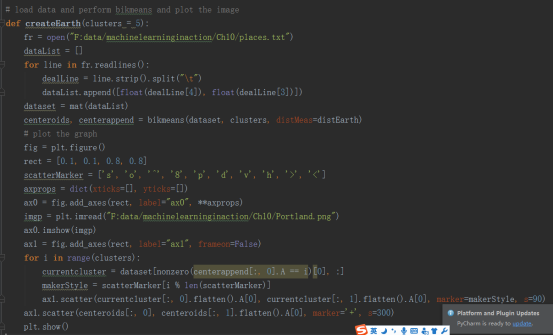
程序的结果如下：

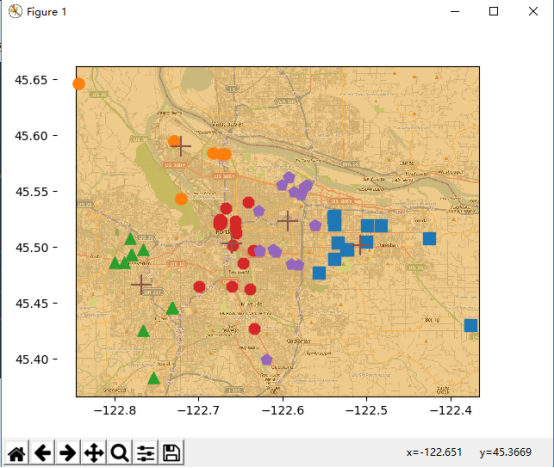
八．总结

聚类算法是一种无监督的算法，常见的聚类算法有k-means算法和二分k-means算法。后者是前者的进阶版，效果也比前者更好。因为k-means算法很容易受到初始点选择的影响，并且很容易陷入局部最小。当然这并不是仅有的聚类算法，聚类算法有很多，还有层次聚类等。

总的来说，聚类算法的目的就是从一堆数据中中无目的的寻找一些簇。这些簇是没有经过事先定义的，但是其确实能够展示出数据中的一些特征。