中国剩余定理+扩展中国剩余定理 讲解+例题（HDU1370 Biorhythms + POJ2891 Strange Way to Express Integers）

0.引子

每一个讲中国剩余定理的人，都会从孙子的一道例题讲起

有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何？

1.中国剩余定理

引子里的例题实际上是求一个最小的x满足

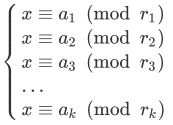
关键是，其中r1，r2，……，rk互质

这种问题都有多解，每一个解都为最小的解加上若干个lcm(r1,r2,...,rk)，这个不用我证了吧（-_-||）

解决这个问题的方法是构造法，

先构造k个数

满足，

这样就保证 ，但是由于 bi 乘了除 ri 以外所有 r，所以bi模其它的 r 都为 0，

再把所有 bi 加起来，得到的数就满足方程了。

例题

UVA756 Biorhythms

HDU1370 Biorhythms

非常裸的一道剩余定理的题，但是某些OJ题面出了问题，以至于让同学们白白wa了很多遍

首先是luogu的翻译，并不是“保证 x 不超过 21252”，而是“保证 x-d 不超过 21252”

然后是（屑）HDU的数据，一开始得输入一个数后才能开始输入，看样例应该就知道了

题目把r1~r3都给出来了，相当于可以直接手算得出

直接代入算b

最后判断x是否<=d，是就+=21252

CODE

#include<cstdio>
#include<cstring>
#include<iostream>
#include<cmath>
#include<queue>
#include<stack>
#include<map>
#include<vector>
#include<algorithm>
#define ENDL putchar('\n')
#define LL long long
#define DB double
#define lowbit(x) ((-x)&(x))
//#define int LL
using namespace std;
inline LL read() {
	LL f = 1,x = 0;char s = getchar();
	while(s < '0' || s > '9') {if(s == '-')f = -1;s = getchar();}
	while(s >= '0' && s <= '9') {x = x * 10 + (s - '0');s = getchar();}
	return x * f;
}
int main() {
//	read();  //HDU的把这句加上
	int p,e,i,d,lc = 21252,ad1 = 5544,ad2 = 14421,ad3 = 1288;
	int Case = 0;
	while(scanf("%d%d%d%d",&p,&e,&i,&d) == 4) {
		if(p == -1 || e == -1 || i == -1 || d == -1) break;
		int x = (p *1ll* ad1 + e *1ll* ad2 + i *1ll* ad3) % lc;
		if(x <= d) x += lc;
		printf("Case %d: the next triple peak occurs in %d days.\n",++ Case,x - d);
	}
	return 0;
}

2.扩展中国剩余定理

这个就比普通中国剩余定理好用多了

还是求这个方程

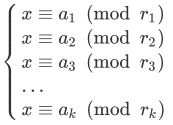
但是不保证互质了

既然不保证互质，他们就有最大公约数

我们依次合并两个方程

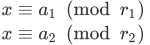
把它变一下，设k、p，满足

即 

移个项：

于是它就变成了“ax+by=c”的形式，可以用扩展欧几里得求出特解k（若无解就整个方程无解了）

它的任意解都满足 

由于x等于通解中的一个，

所以

成功合并成一个方程！

最后剩下一个方程时，最小的解就为式子右边的值

例题

POJ2891 Strange Way to Express Integers

这题是扩展中国剩余定理的板题，不用我讲了吧（众所周知，板题≠水题）

CODE

#include<cstdio>
#include<cstring>
#include<iostream>
#include<cmath>
#include<queue>
#include<stack>
#include<map>
#include<vector>
#include<algorithm>
#define MAXN 2000005
#define MAXM 3000005
#define ENDL putchar('\n')
#define LL long long
#define DB double
#define lowbit(x) ((-x)&(x))
#define int LL
using namespace std;
inline LL read() {
	LL f = 1,x = 0;char s = getchar();
	while(s < '0' || s > '9') {if(s == '-')f = -1;s = getchar();}
	while(s >= '0' && s <= '9') {x = x * 10 + (s - '0');s = getchar();}
	return x * f;
}
const int jzm = 1000000007;
int n,m,i,j,s,o,k;
LL exgcd(LL a,LL b,LL &x,LL &y) {
	if(b == 0) {
		x = 1;y = 0;
		return a;
	}
	LL r = exgcd(b,a%b,y,x);
	y -= x*(a/b);
	return r;
}
signed main() {
	while(scanf("%lld",&n) == 1) {
		LL r1 = read(),a1 = read();
		bool flag = 1;
		for(int i = 2;i <= n;i ++) {
			LL r2 = read(),a2 = read(),k,p;
			if(a2 > a1) swap(a1,a2),swap(r1,r2);
			if(!flag) continue;
			LL gc = exgcd(r1,r2,k,p),lc = r1 / gc * r2;
			if((a1-a2) % gc) {
				flag = 0;continue;
			}
			LL tym = r2/gc;
			((k = (k * (a1-a2) / gc) % tym) += tym) %= tym;
			a1 = (a1 + lc - k * r1 % lc) % lc;
			r1 = lc;
		}
		if(!flag) printf("-1\n");
		else printf("%lld\n",a1 == 0 ? r1:a1);
	}
	return 0;
}