[*]Is L2 Physics-Informed Loss Always Suitable for Training Physics-Informed Neural Network?

NeurIPS 2022

本篇工作对PINN中的物理损失进行了探究，作者认为L2损失并不总是适用于训练PINN。并从PDE解的稳定性角度给出了理论性的说明。读了这篇文章，感觉自己的毕业论文做的十分浅显。顶会文章的质量很不错，有理论支持，实验工作量也丰富。

本文的视角从PDE中稳定性的概念入手，来研究当损失接近0时学习解的渐近行为。证明了对于一般的Lp损失，只有p足够大时，一类宽的HJB方程才是稳定的。因此，使用L2损失并不适合于这类方程，L∞损失才是更合适的选择。作者提出了一种类似对抗训练精神的方法，来解决发现的问题。本文主要考虑高阶HJB方程。

在目前PINN的问题中，当L2损失等于0时，学习到的解就等价于精确解，这是自然的。但是，目前在实践中更常见的，具有小的但是非零损失的学习解的质量，目前仍然没有任何的近似保证。因此作者关心一个基础的问题：能否保证具有较小的物理信息损失的学习解始终对应于精确解的良好近似器？所以作者引出了稳定性，从稳定性的角度分析这个问题。此前的工作在面对PINN训练失败时，将目光集中到复杂的优化域和损失项之间的不可比较性。

文章在PINN的框架下分析PDE的稳定性，稳定性表征当物理信息损失接近0时，学习解和精确解之间的渐近距离。如果PDE在某些损失函数下不稳定，那我们可能就无法通过最小化损失来获得良好的近似解。本文证明了这类方程需要Lp损失中p足够大。L2损失并不适合于这类方程，因为所学习到的解会任意的远离精确解。稳定性从形式上表征了当一个微小扰动改变算子、初始条件、边界条件时，PDE解的行为。方程是稳定的，如果扰动PDE的解在扰动接近零是收敛到精确解。

本文针对的高阶HJB方程，理论结果表明L∞会是更好的选择。受到这一点的启发，作者提出了一种新的算法用来训练PINN，采用最小最大优化进程来最小化L∞损失。具体的方法将在后面介绍。

由于神经网络的能力或者优化过程中的随机性，损失项并不会完全收敛到0。所以我们要考虑具有小损失的解是否是精确解的一个好的近似？这个问题等价于PDE中稳定性的概念。我们了解到：一些高阶HJB方程是稳定的，但不是L2稳定的，也就是L2物理信息损失将会失败于去寻找解。理论结果如下：

更重要的是，理论结果表明，物理信息损失的设计也发挥着重要的作用对于使用PINN求解PDE。

使用对抗训练求解HJB方程

目标函数是：

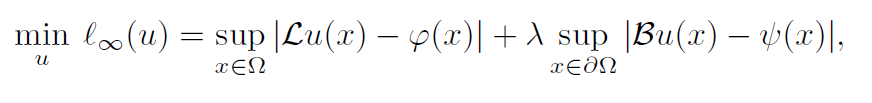
这个目标项可以看作一个最小最大问题，内循环是寻找损失最大的数据点，分别在域内和边界上，外循环上是最小化问题，寻找u使得总损失最小。

在每次循环中，模型参数和数据点都会更新。为了获得等效的L∞损失（也就是令p足够大），作者使用最大损失的方法。方法如下：

所提出方法的伪代码如下：

通过内循环找到损失最大的点，然后再利用任何的一阶方法进行优化（这就等效于L无穷范数的损失）。

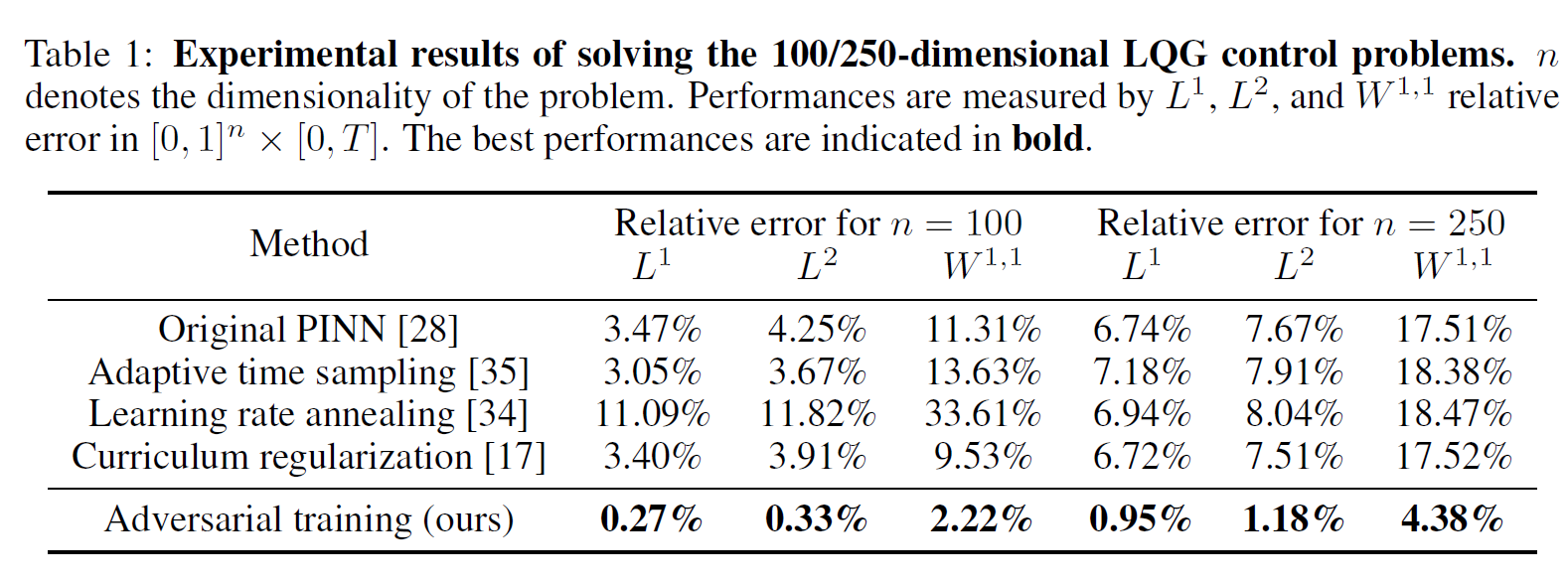
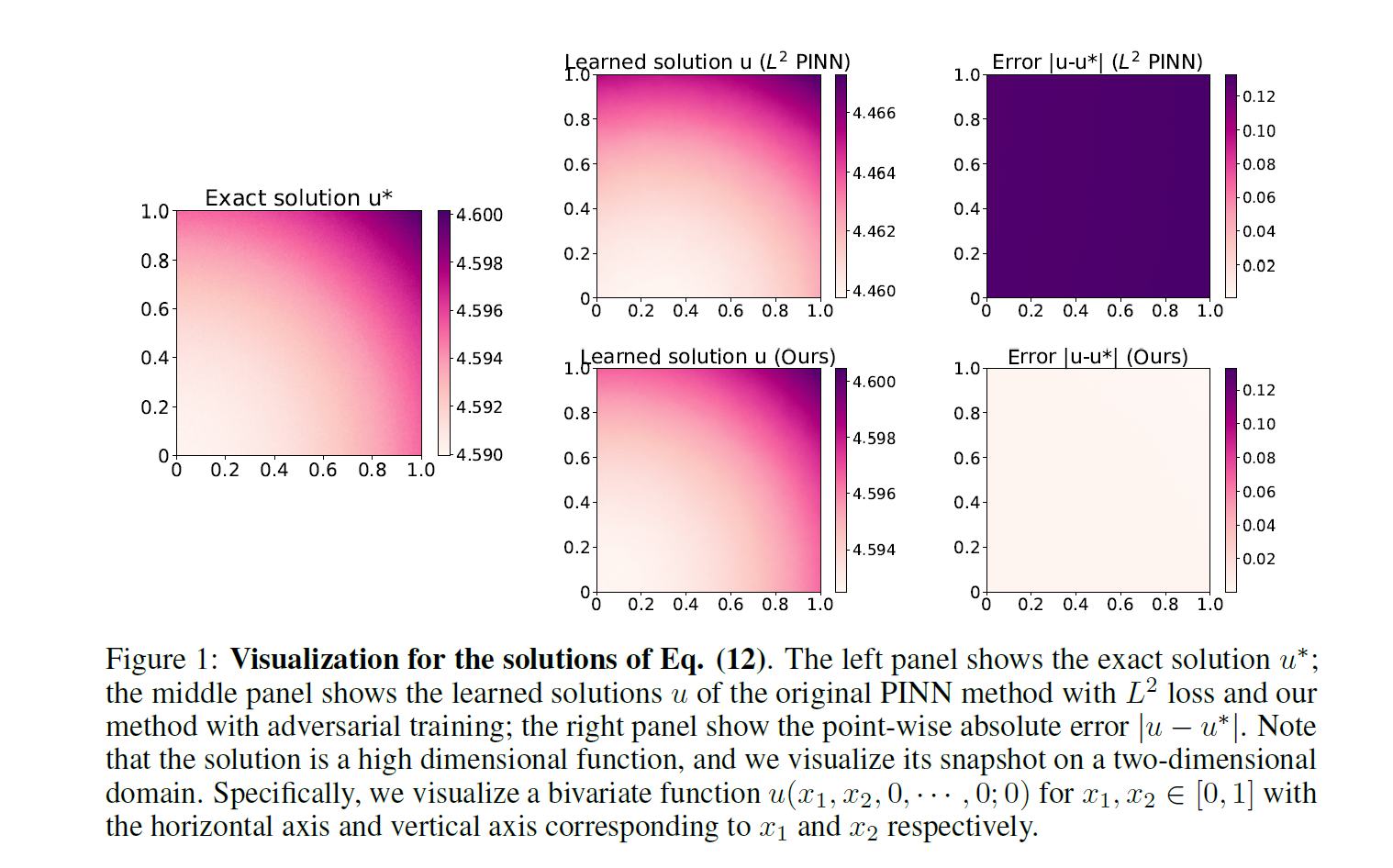
实验结果如下，提升的幅度还是很大的。