CF632(div.2)C. Eugene and an array

https://codeforces.ml/contest/1333/problem/C

大概题意是规定和为0的数组为不合格数组，询问给定数组中共有多少个合格子数组。

解题

子数组的数量

一个长度为 \(n\) 的数组 \(a[0,n-1]\)，选取 \(i\) 作为子数组的终点，那么我们可以选取 \([0,i]\) 中的任何一个 \(j\) 作为起点，这样可以得到子数组 \(a[j,i]\) ，所以以 \(i\) 为终点的子数组有 \(i+1\) 种。以此类推，最终子数组的总个数为 \(count=\sum_{i=0}^{n-1}(i+1)= (n+1)*n/2\) 。

合格子数组的数量

根据题意可得，如果一个数组是不合格的（存在子数组和为0），则含有这个数组的所有父亲数组都是不合格的。

当我们以 \(i\) 为子数组终点时。

如果子数组 \(a[p_1,p_2](p_2\le i)\) 是不合格数组，那么我们只能在 \((p_1,i]\) 区间内选取起点 \(j\) （共 \(i-p_1\) 种），否者新数组会成为不合格部分的父亲数组。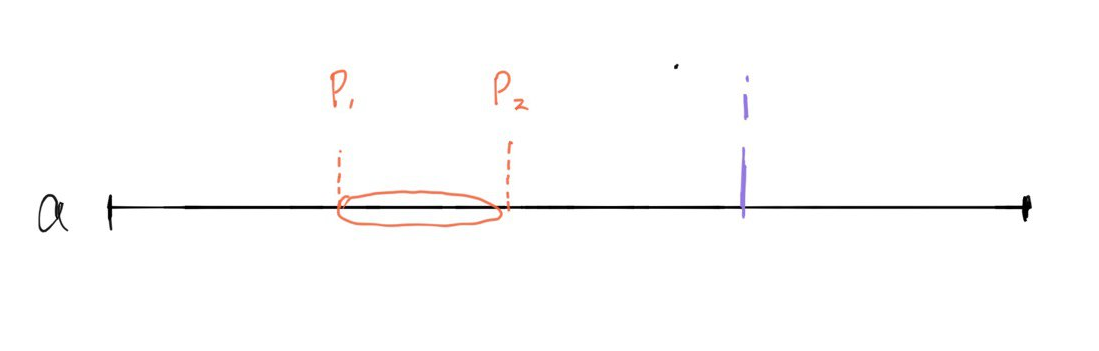

如果 \(p_2 \gt i\) 的话，则可以在 \([0,i]\) 区间内选取起点 \(j\)，共计 \(i+1\) 种。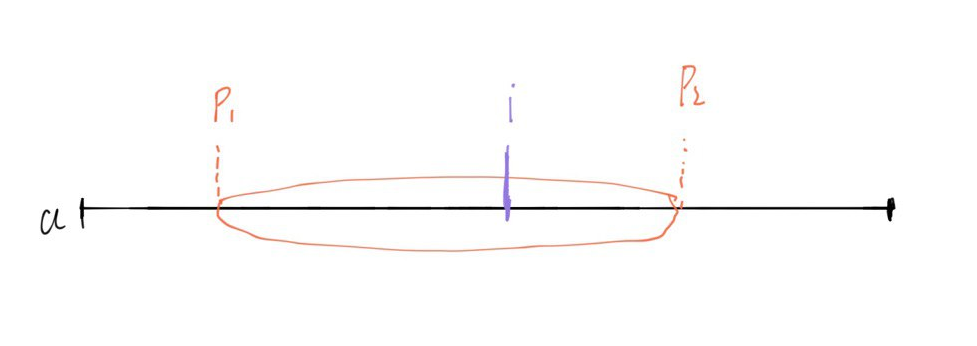

我们设 \(s\) 为所有出现在位置 \(i\) 之前的不合格子数组的起点位置的集合。设 \(f(i)\) 为以 \(a_i\) 为结尾的合格子数组个数，\(f(i) = i-max\{p|p<i,p\in s\}\)，如果 \(p\) 不存在，那么 \(f(i) = i+1\)。

全部合格子数组的数量 \(ans = \sum_{all}f(i)\)，不会重复计算。

代码

#include<bits/stdc++.h>
#define ll long long

#define fr(i,n) for(int i=0;i<n;i++)
#define frs(i,n,flag)   for(int i=0;i<n&&flag;i++)

#define frr(i,j,n) for(int i=j;i<n;i++)
#define r_frr(i,j,n) for(int i=n-1;i>=j;i--)

#define frrs(i,j,n,flag)    for(int i=j;i<n&&flag;i++)
#define r_frrs(i,j,n,flag)    for(int i=n-1;i>=j&&flag;i--)

#define arend(i,n) ((i!=n-1)?" ":"\n")
#define memset0(dp) memset(dp,0,sizeof(dp))
#define print_arr(begin,end)    for(auto it = begin;it!=end;it++)  cout<<*it<<arend(it,end);
#define log_this(name,value)    cout<<name<<": "<<value<<endl;
#define e4 10004#define e5 100005#define e6 1000006#define e7 10000007#define e9 1000000000#define INF 9999999
using namespace std;
int     to_int(string s)    {stringstream ss;ss<<s;int a;ss>>a;return a;}
string  to_str(double a)    {stringstream ss;ss<<a;return ss.str();}

int main(){

    cin.tie(0);
    //ios::sync_with_stdio(false);
    //cout<<setiosflags(ios::fixed)<<setprecision(0);

    //freopen("1.out","w",stdout);

    int n;
    while(cin>>n){
        ll sum=0,p=-1,ans=0,inp;
        map<ll,ll>loc;loc[0] = 0;
        fr(i,n){
            cin>>inp;
            sum += inp;
            auto it = loc.find(sum);
            if(it!=loc.end()){
                p = max(p,loc[sum]);
            }
            loc[sum] = i+1;
            ans += i - p;
        }
        cout<<ans<<endl;
    }
    return 0;
}