剑指Offer-34.数组中的逆序对(C++/Java)

题目：

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P%1000000007

输入描述:

题目保证输入的数组中没有的相同的数字

数据范围：

对于%50的数据,size<=10^4

对于%75的数据,size<=10^5

对于%100的数据,size<=2*10^5

分析：

可以从头扫描整个数组，每扫描到一个数字，就去计算后面的数字有多少比它小，这样操作的话时间复杂度是O(n^2)，应该会超时。

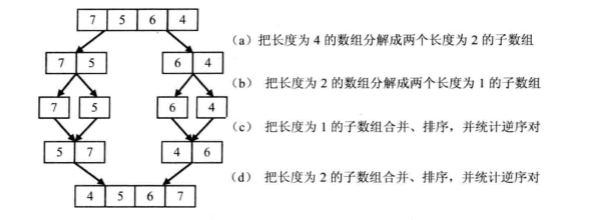
我们可以利用归并排序时合并两个有序的数组时候，更快的求得每次合并时的逆序对。

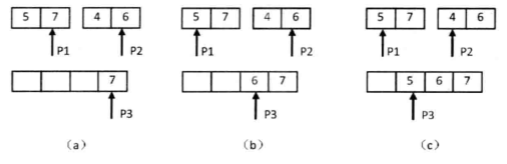
例如合并[5,7]和[4,6]时从两个数组后面开始比较，选出较大的元素。

因为7>6，所以7一定大于第二个数组剩下的所有元素，因为数组本身是有序的，可以立刻得到逆序对的个数，当后面的元素大时，不需要统计逆序对的个数，因为此时要大于前面剩下的所有元素，不构成逆序对。基于这种方法，时间复杂度控制在O(nlogn)。

程序：

C++

class Solution {
public:
    int InversePairs(vector<int> data) {
        return mergesort(data, , data.size()-)%;
    }
    long long mymerge(vector<int> &vec, int left, int mid, int right){
        vector<int> temp(right-left+,);
        int index = right-left;
        long long countnum = ;
        int i = mid;
        int j = right;
        while(i >= left && j >= mid+){
            if(vec[i] > vec[j]){
                countnum += (j-mid);
                temp[index--] = vec[i--];
            }
            else{
                temp[index--] = vec[j--];
            }
        }
        while(i >= left)
            temp[index--] = vec[i--];
        while(j >= mid+)
            temp[index--] = vec[j--];
        for(int i = ; i < temp.size(); ++i)
            vec[i+left] = temp[i];
        return countnum;
    }
    long long mergesort(vector<int> &vec, int left, int right){
        if(left >= right)
            return ;
        int mid = (left + right) / ;
        long long leftCount = mergesort(vec, left, mid);
        long long rightCount = mergesort(vec, mid+, right);
        long long res = mymerge(vec, left, mid, right);
        return res + leftCount + rightCount;
    }
};

Java

public class Solution {
    public int InversePairs(int [] array) {
        return (int)(mergesort(array,  , array.length-)%);
    }
    public static long mymerge(int [] array, int left, int mid, int right){
        int[] temp = new int[right-left+];
        int index = right-left;
        long countnum = ;
        int i = mid;
        int j = right;
        while(i >= left && j >= mid+){
            if(array[i] > array[j]){
                countnum += (j-mid);
                temp[index--] = array[i--];
            }
            else{
                temp[index--] = array[j--];
            }
        }
        while(i >= left)
            temp[index--] = array[i--];
        while(j >= mid+)
            temp[index--] = array[j--];
        for(i = ; i < temp.length; ++i)
            array[i+left] = temp[i];
        return countnum;
    }
    public static long mergesort(int [] array, int left, int right){
        if(left >= right)
            return ;
        int mid = (left + right) / ;
        long leftCount = mergesort(array, left, mid);
        long rightCount = mergesort(array, mid+, right);
        long res = mymerge(array, left, mid, right);
        return res + leftCount + rightCount;
    }
}