C++做四则运算的MFC计算器（二）栈转换和计算后缀表达式

上篇写了MFC界面搭建，这篇写实现计算。涉及到数据结构，对新手很不友好。

虽然是MFC程序，但是能灵活地分离后台代码，自行构建控制台程序，本文的程序一开始只是个“黑框框”程序，后来把代码包装进MFC的。

上篇文章链接：C++做四则运算的MFC计算器（一）MFC界面创建

概要：

1. 中缀表达式与后缀表达式
2. 栈的相关实现
3. 用栈将中缀表达式转换成后缀表达式
4. 用栈计算后缀表达式
5. 等号按钮功能，显示计算结果

中缀表达式与后缀表达式

中缀：（60-20）/（5-1）。小学就学的东西

后缀：60 20 – 5 1 - /，为增加可读性，以“#”做分隔符，60#20#-#5#1#-#/。

后缀计算：从左到右遇到符号就计算符号左边的两个数并写上新值，即优先的运算符相对在左。上例中遇到第一个‘-’算60-20得40，遇到第二个“-”计算5-1得4，遇到“/”计算30/3的10，结果是10。

对比：中缀式人看起来方便，后缀式没有括号，计算顺序从前到后，用计算机操作起来的逻辑简单。

栈的相关实现

输入的值都是字符，所以需要一个字符结构的栈；在计算数时还需要一个处理数字结构的栈。

字符和数值的栈结构体分别命名SqStack和SqStackN。

然后实现栈初始化、进栈、出栈等栈的操作函数。

在工程中，同时把栈结构体和操作函数声明在新建的头文件xxx.h中，或者工程中其他头文件如stdafx.h，新建一个cpp文件实现函数体。

这里的栈和操作函数是自己动手定义的，可以直接用STL中的栈，比较方便。

 struct SqStack {
     char data[maxsize];
     int top;
 };
 struct SqStackN {
     double data[maxsizen];
     int top;
 };
 //栈操作函数—字符
 void initStack(SqStack *&s);
 bool Push(SqStack *&s, char e);
 bool Pop(SqStack *&s, char &e);
 bool GetTop(SqStack *s, char &e);
 void DestroyStack(SqStack *&s);
 bool StackEmpty(SqStack *s);
 //栈操作函数—数字
 void initStack(SqStackN *&s);
 bool Push(SqStackN *&s, double e);
 bool Pop(SqStackN *&s, double &e);
 bool GetTop(SqStackN *s, double &e);
 void DestroyStack(SqStackN *&s);
 bool StackEmpty(SqStackN *s);

 //后缀表达式转换函数
 void trans(char* exp, char postexp[]);
 //计算后缀表达式函数
 double calculate(char* postexp);

头文件主要声明

 void initStack(SqStack *&s) {
     s = new SqStack();
     s->top = -;
 }
 bool Push(SqStack *&s, char e) {
     if (s->top == maxsize-)
         return false;
     s->top++;
     s->data[s->top] = e;
     return true;
 }
 bool Pop(SqStack *&s, char &e) {
     if (s->top == -)
         return false;
     e = s->data[s->top];
     s->top--;
     return true;
 }
 bool GetTop(SqStack *s, char &e) {
     if (s->top == -)
         return false;
     e = s->data[s->top];
     return true;
 }
 void DestroyStack(SqStack *&s) {
     free(s);
 }
 bool StackEmpty(SqStack *s) {
     return (s->top == -);
 }

 void initStack(SqStackN *& s){
     s = new SqStackN();
     s->top = -;
 }

 bool Push(SqStackN *& s, double e)
 {
     if (s->top == maxsizen - )
         return false;
     s->top++;
     s->data[s->top] = e;
     return true;
 }

 bool Pop(SqStackN *& s, double & e)
 {
     if (s->top == -)
         return false;
     e = s->data[s->top];
     s->top--;
     return true;
 }

 bool GetTop(SqStackN * s, double & e)
 {
     if (s->top == -)
         return false;
     e = s->data[s->top];
     return true;
 }

 void DestroyStack(SqStackN *& s){
     free(s);
 }

 bool StackEmpty(SqStackN * s)
 {
     return (s->top == -);
 }

cpp函数定义

用栈将中缀表达式转换成后缀表达式

从左向右扫描中缀，遇到数字就添加到后缀中，遇到运算符进行栈处理，而栈的处理依赖于运算符优先级，优先级高的靠近栈顶，保证在后缀式中先运算的运算符靠前。结束后后缀式仍是字符数组。

写个函数tans()，有2个参数char * exp和char postexp[ ]，

先初始化一个字符栈指针s，char e用来操作栈顶元素，int p作为postexp数组的下标。用循环扫描exp

while (*exp != '\0') {switch(*exp){case:case:case:default}......}

扫描到数字字符时直接加到后缀式中，并加上 ‘ # ’ 以分割。

其他情况无非是+、-、*、/、(、)这6个符号。

(、)优先级最高，在括号之间的运算符一定比括号之外的优先运算，遇到 ‘ ( ’ 即进栈，遇 ‘ ) ’ 即出栈栈顶元素直到出来的是 ‘ ( ’ 。因此栈中不会有 ‘ ) ’ 。

*、/优先级其次，先判断栈顶是什么，栈顶是*、/则将其出栈到后缀式，栈顶是+、-则将 ‘ * ’ 或 ‘ / ’ 进栈，保证后缀中乘和除的优先运算。

+、-优先级最低，这是栈顶元素不管是+-*/都出栈至后缀式，但栈顶是 ‘ ( ’ 时就不需要出栈，‘ ( ’可以看作是一个新的运算起点，将+或-进栈即可。

exp扫描后栈可能还会有运算符，将剩下的都出栈至后缀式。再为后缀式加结束标识 ‘\0’ ，销毁栈释放空间。

 void trans(char* exp,char postexp[]) {
     char e;
     SqStack *s;    initStack(s);    // 即SqStack s = new SqStacck()
     int p = ;//postexp的下表
     while (*exp != '\0') {
         switch (*exp)
         {
         case '+':
         case '-':
             while (!StackEmpty(s)) {
                 GetTop(s, e);
                 if (e != '(') {
                     postexp[p++] = e;
                     Pop(s, e);
                 }
                 else
                     break;
             }
             Push(s, *exp);
             exp++;break;
         case '*':
         case '/':
             while (!StackEmpty(s)) {
                 GetTop(s, e);
                 if (e == '*' || e == '/') {
                     postexp[p++] = e;
                     Pop(s, e);
                 }
                 else
                     break;
             }
             Push(s, *exp);
             exp++;break;
         case '(':
             Push(s, *exp);
             exp++;break;
         case ')':
             Pop(s, e);
             while (e != '(') {
                 postexp[p++] = e;
                 Pop(s, e);
             }
             exp++;break;
         default:
             while (*exp >= ''&&*exp <= '') {
                 postexp[p++] = *exp;
                 exp++;
             }
             postexp[p++] = '#';
             break;
         }
     }
     while (!StackEmpty(s)) {
         Pop(s, e);
         postexp[p++] = e;
     }
     postexp[p] = '\0';
     DestroyStack(s);
 }

转换函数trans()

栈计算后缀表达式

这一功能相对简单些，扫描后缀式，

遇到表示数字的字符时，例如 ‘ 6 ’ ，利用它与 ‘ 0 ’ 编码之间的差得到数字，‘ 6 ’ - ‘ 0 ’ = 6 ，乘10实现位数值。得到的数值放入栈里。

遇到运算符时直接出栈两个元素，此时这两个元素一定是数字，第一个出栈的做运算符右值，第二个做左值，顺序不能反，结果还要入栈以进行下一步运算。

遇到 ‘ / ’ 时还要判断栈顶是否是0，被除数可不能是0。

最后栈中就是运算结果，出栈作为返回值。

 double calculate(char* postexp) {
     double a, b,c,d,e;
     SqStackN *o;    initStack(o);
     while (*postexp != '\0') {
         switch (*postexp)
         {
         case '+':
             Pop(o, a);
             Pop(o, b);
             c = b + a;
             Push(o, c);
             break;
         case '-':
             Pop(o, a);
             Pop(o, b);
             c = b - a;
             Push(o, c);
             break;
         case '*':
             Pop(o, a);
             Pop(o, b);
             c = b * a;
             Push(o, c);
             break;
         case '/':
             Pop(o, a);
             Pop(o, b);
             if (a != ) {
                 c = b / a;
                 Push(o, c);
                 break;
             }
             else {
                 exit();
             }
             break;
         default:
             d = ;
             while (*postexp >= ''&&*postexp <= '') {
                 d = d *  + (*postexp - '');
                 postexp++;
             }
             Push(o, d);
             break;
         }
         postexp++;
     }
     GetTop(o, e);
     DestroyStack(o);
     return e;
 }

计算后缀式函数

等号按钮功能-计算结果显示

运算功能已经实现了，但是要讲功能绑定到 ‘ = ’ 还有最后一道坎

MFC文本编辑框的类型是CString，要想转换成char[]有点让人头大。

需要几个变量，输入的算式char exp[50]，后缀式char postexp[50]，运算结果result。

CString转换为char[]直接上代码吧： ::wsprintfA(exp, "%ls", (LPCTSTR)editv);

double转CString代码： resultv.Format(_T("%.5lf"), result);

目前发现处理CString有些问题，VS2017可以正常处理，旧点版本的IDE不支持这里的处理方法。

 void CMFCcalculationDlg::OnBnClickedButton19()
 {
     // TODO: 等号按钮
     char exp[];
     char postexp[];
     double result;
     UpdateData(true);
     ::wsprintfA(exp, "%ls", (LPCTSTR)editv);
     trans(exp, postexp);
     result = calculate(postexp);
     resultv.Format(_T("%.5lf"), result);
     //resultv.Format(TEXT("%lf\n%.2lf"), result);
     UpdateData(false);
 }

等号按钮功能

运行结果：

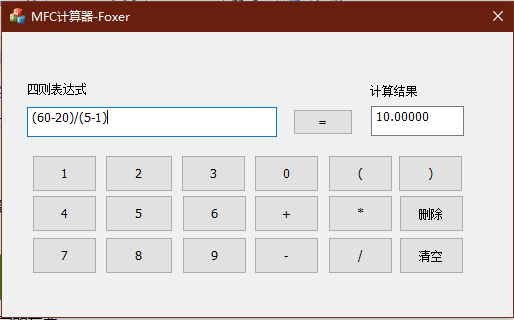
程序在未发布前比较大，100多M，包含了很多不用的文件，在资源管理器里还是隐藏的。发布后的程序只有几M。

程序发布：将Debug改成Release，运行即发布，之后项目同级目录里有Release文件夹，里面就是你的应用程序。