以太网驱动的流程浅析(二)-Ifconfig的详细代码流程【原创】

以太网驱动流程浅析（二）-ifconfig的详细代码流程

Author：张昺华
Email：920052390@qq.com
Time：2019年3月23日星期六

此文也在我的个人公众号以及《Linux内核之旅》上有发表：以太网驱动流程浅析（二）-ifconfig的详细代码流程

很喜欢一群人在研究技术，一起做有意思的东西，一起分享技术带给我们的快乐，也希望中国有更多的人热爱技术，喜欢一起研究、分享技术，然后可以一起用我们的技术来做一些好玩的东西，可以为这个社会创造一些东西来改善人们的生活。

如下是本人调试过程中的一点经验分享，以太网驱动架构毕竟涉及的东西太多，如下仅仅是针对加载流程和围绕这个问题产生的分析过程和驱动加载流程部分，并不涉及以太网协议层的数据流程分析。

【硬件环境】 Imx6ul

【Linux kernel版本】 Linux4.1.15

【以太网phy】 Realtek8201f

1. 以太网流程分析跟踪

1.1 Ifconfig的详细代码流程

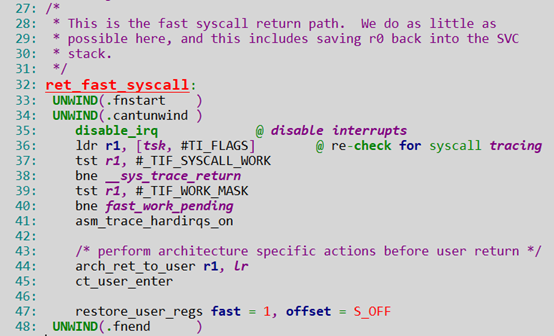
ret_fast_syscall ===》这是返回系统调用的syscall，大家可以看注释，saving r0，back into the SVC stack
arch/arm/kernel/entry-common.S

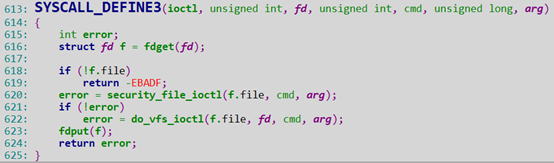
fs/ioctl.c

通过dump信息，我们知道是调用了vfs_ioctl，

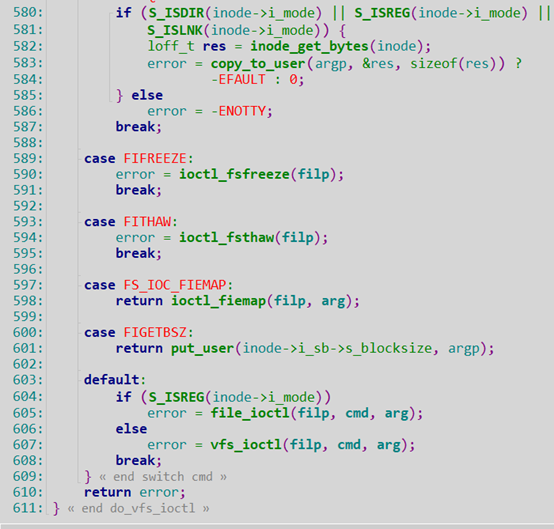
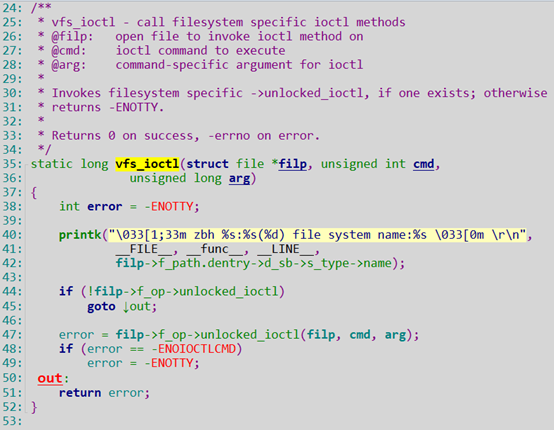
继续看vfs_ioctl：

打印的目的是告诉大家一个查看文件系统类型的方法。
这个是属于vfs下的sockfs文件系统
到了这里我们要找到unlocked_ioctl的回调函数是哪个
方法一：

方法二：
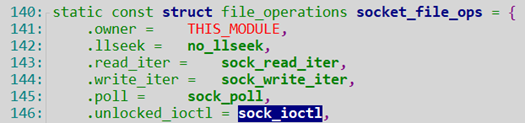
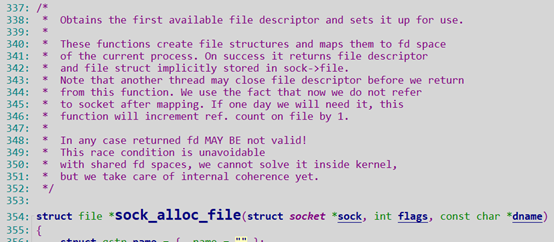
因为我们在kernel的dump信息里面知道是调用了sock_ioctl，所以我们直接去找这个函数就好了，net/socket.c

注册是在如下地方注册的：

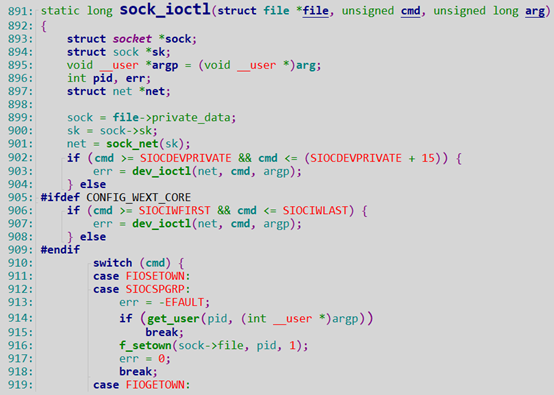
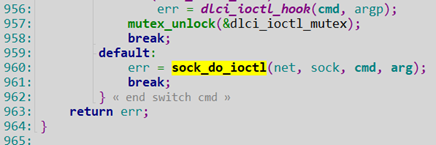
看下sock_ioctl代码：

我们可以得出err是-19，
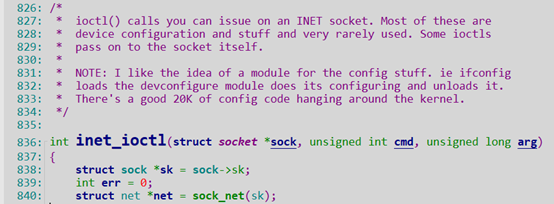
这里的sock->ops->ioctl回调的是inet_ioctl, 路径：net/ipv4/af_inet.c

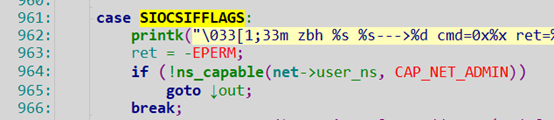
调到了devinet_ioctl，路径：net/ipv4/devinet.c

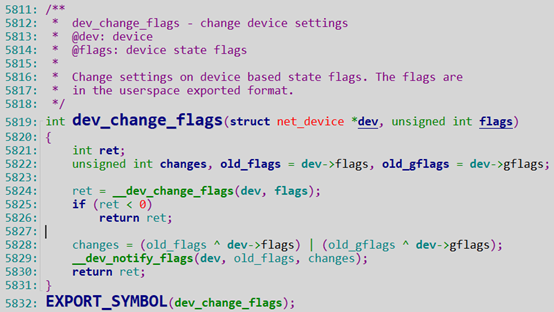
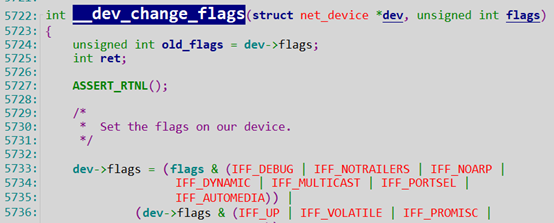
继续跟踪dev_change_flags，路径：net/core/dev.c

到这里大家有印象了吧？__dev_open最终回调的是控制器驱动fec_main.c中的那个
fec_enet_open，大家还记得我们要分析什么吧？那个-19的错误就是这个open里面返回的
我们继续看这个最底层实现。

2. 网址分享

http://stackoverflow.com/questions/5308090/set-ip-address-using-siocsifaddr-ioctl
http://www.ibm.com/support/knowledgecenter/ssw_aix_72/com.ibm.aix.commtrf2/ioctl_socket_control_operations.htm
https://lkml.org/lkml/2017/2/3/396
linux PHY驱动
http://www.latelee.org/programming-under-linux/linux-phy-driver.html
Linux PHY几个状态的跟踪
http://www.latelee.org/programming-under-linux/linux-phy-state.html
第十六章PHY -基于Linux3.10
https://blog.csdn.net/shichaog/article/details/44682931

```

End