[学习笔记] 可持久化线段树&主席树

众所周知,线段树是一个非常好用也好写的数据结构,

因此,我们今天的前置技能:线段树.

然而,可持久化到底是什么东西?

别急,我们一步一步来...

step 1

首先,一道简化的模型:

给定一个长度为\(n\)的序列,\(m\)个操作,支持两种操作:

• 修改某个点\(i\)的权值
• 查询历史上某个版本\(u\)中点\(i\)的权值

同时,每个操作都会生成一个新的版本(也就是说修改是改的一个新的版本,而查询是直接\(copy\)上一个版本.

那么,暴力的做法来了:

直接维护\(m\)棵线段树,先\(copy\)一遍,再直接修改/查询.

然而时间空间都得炸啊啊啊

别急,让我们仔细想想...

首先,我们考虑一下每次修改会发生什么(看图):

(其中修改的是6号节点,红色是经过的路径),

我们可以发现,每次修改都只改了一条链.

也就是说,对于上一个版本,就只有一条链不一样(查询就是一模一样了).

因此,对于上一个版本中一样的其他的链,我们就可以直接沿用.

比如说,上一个版本长这样:

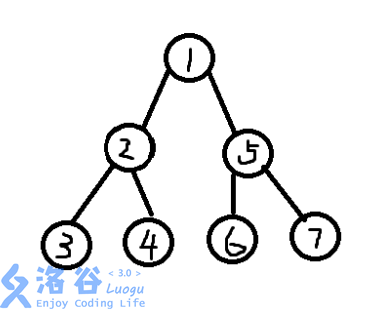
而沿用后的图就长这样选点时的随意导致了图片的丑陋:

那么,我们就只需要在更新版本时,新建一个根节点\(rt[i]\),

并且只需要新建修改的那条链,其他的沿用上一个版本的就行了.

代码也很简单:

void update(int &k/*动态加的点(当前节点)*/,int p/*沿用的点,即上个版本中这个位置的节点编号*/,int l,int r,int pla/*修改的元素位置*/,int x/*修改的权值*/){
	k=++tot;t[k]=t[p];//先copy一波
	if(l==r){t[k].val=x;return ;}
	int mid=(l+r)>>1;//这里就和线段树一样了
	if(pla<=mid) update(t[k].l,t[p].l,l,mid,pla,x);
	else update(t[k].r,t[p].r,mid+1,r,pla,x);
}

顺便把建树和询问也贴上来吧(其实和线段树一样):

void build(int &x,int l,int r){
	x=++tot;
	if(l==r){t[x].val=a[l];return ;}
	int mid=(l+r)>>1;
	build(t[x].l,l,mid);build(t[x].r,mid+1,r);
}

int query(int p,int l,int r,int x){
	if(l==r) return t[p].val;
	int mid=(l+r)>>1;
	if(x<=mid) return query(t[p].l,l,mid,x);
	else return query(t[p].r,mid+1,r,x);
}

到这里,一个简单的模板就结束啦.

例题:[模板]可持久化数组

这题就和模板一模一样,

在叶子节点记录权值,每次单点修改即可.

注意一下,询问是复制的询问的那个版本(不是上一个)因为这个调了好久qwq

上完整代码吧其实都在上面了~:

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;

inline int read(){
	int sum=0,f=1;char c=getchar();
	while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
	while(c<='9'&&c>='0'){sum=sum*10+c-'0';c=getchar();}
	return sum*f;
}

const int MX=1000005;
struct tree{int l,r,val;}t[MX*30];
int n,m,a[MX];
int rt[MX],tot=0;

void build(int &x,int l,int r){
	x=++tot;
	if(l==r){t[x].val=a[l];return ;}
	int mid=(l+r)>>1;
	build(t[x].l,l,mid);build(t[x].r,mid+1,r);
}

void update(int &k,int p,int l,int r,int pla,int x){
	k=++tot;t[k]=t[p];
	if(l==r){t[k].val=x;return ;}
	int mid=(l+r)>>1;
	if(pla<=mid) update(t[k].l,t[p].l,l,mid,pla,x);
	else update(t[k].r,t[p].r,mid+1,r,pla,x);
}

int query(int p,int l,int r,int x){
	if(l==r) return t[p].val;
	int mid=(l+r)>>1;
	if(x<=mid) return query(t[p].l,l,mid,x);
	else return query(t[p].r,mid+1,r,x);
}

int main(){
	n=read();m=read();
	for(int i=1;i<=n;i++) a[i]=read();
	build(rt[0],1,n);
	for(int i=1;i<=m;i++){
		int tt=read(),opt=read(),pla=read();
		if(opt==1){int x=read();update(rt[i],rt[tt],1,n,pla,x);}
		else if(opt==2){printf("%d\n",query(rt[tt],1,n,pla));rt[i]=rt[tt];}
	}
	return 0;
}

step 2

接下来,就是我们喜闻乐见的主席树了(话说有哪位\(dalao\)能告诉我为什么叫这名字?).

我们以一道模板题开始吧:[模板]可持久化线段树 1(主席树)

给出一个长度为\(n\)的序列,\(m\)个询问,每次询问区间\([l,r]\)中第\(k\)小的数.

这题暴力很好写吧(然而我们并不满足于暴力).

我们还是一步步来,

首先,先考虑下如果是区间\([1,n]\)的第\(k\)小该怎么做:

这时候,我们可以考虑到权值线段树.

将原序列离散化,再建一棵线段树,

但这个线段树维护的区间并不是序列的区间,

而是权值的区间.

比如说区间\([l,r]\),其实指的是离散化后的权值\(l\)~\(r\),

也就是第\(l\)大到第\(r\)大.

还是举个栗子吧:

假设我们现在有一个序列\(a\):1,3,3,5,5,5,8,8,8,8.

那么离散化以后就是:1,2,2,3,3,3,4,4,4,4.

然后我们再建一棵权值线段树:

其中黑色的代表节点编号,红色的代表权值区间,

而蓝色的是接下来我们要讲的每个节点维护的一个值:\(cnt\).

这个\(cnt\)表示的是当前节点的权值区间内有几个节点.

听不懂?没关系我们接着看:

当我们讲第一个元素(在离散化后就是\(1\))插入以后,树就变成了这样:

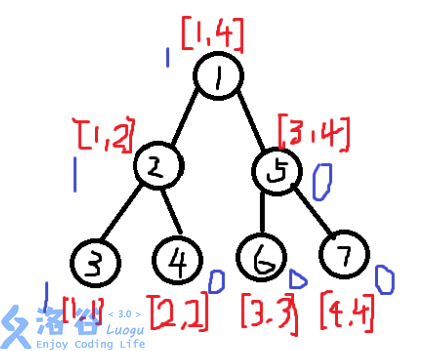
所有权值区间包括\(1\)的\(cnt\)都加了\(1\).

而当我们将所有数都插进去后,树就成了这样:

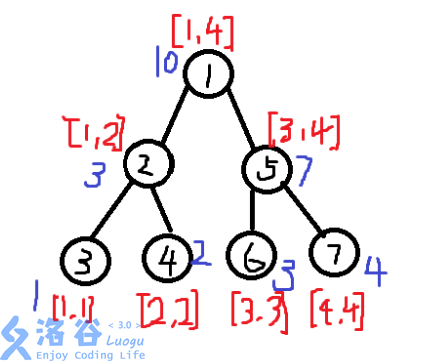
于是,我们就可以清楚地看到,在序列中,权值在区间\([l,r]\)的数有多少个.

插入的代码如下:

int update(int p/*节点编号*/,int l,int r/*l,r为权值区间*/,int k/*插入的权值*/){
    int x=++tot;t[x]=t[p];t[x].cnt++;
    if(l==r) return x;
    int mid=(l+r)>>1;
    if(k<=mid) t[x].l=build(t[p].l,l,mid,k);
    else t[x].r=build(t[p].r,mid+1,r,k);
    return x;
}

然后我们在求第\(k\)小时,先与左子树的\(cnt\)比较,

若\(k<=cnt\),那答案就在左子树的权值区间里,

否则,将\(k\)减去\(cnt\),再在右子树里找,

一直到最底层就行了.

查询代码如下:

int query(int p/*当前节点*/,int l,int r,int k/*第k小*/){
	if(l==r) return l;
	int mid=(l+r)>>1;
	if(k<=t[t[p].l].cnt) return query(t[p].l,l,mid,k);
	else return query(t[p].r,mid+1,r,k-t[t[p].l].cnt);
}

那么接下来,我们来考虑区间\([l,r]\)的第\(k\)小:

仔细想想,其实我们可以用前缀和的思想,

一个权值为\(x\)的数在\(1\)~\(l-1\)中出现了\(a\)次,

在\(1\)~\(r\)中出现了\(b\)次,

那么它在区间\([l,r]\)中就出现了\(a-b\)次.

因此,我们可以对每个区间\([1,i],i\in [1,n]\)建一颗权值线段树,

在查询时,用前缀和的思想计算\(cnt\),再查找就行啦.

然而到这里就结束了吗?

我们注意到,对于区间\([1,i]\)的权值线段树,

与区间\([1,i-1]\)比起来仅仅是多插入了一个\(i\)的权值而已.

想到了什么? 可持久化线段树!

没错,我们可以像可持久化线段树一样,

沿用相同的节点,只新建需要更新的一条链就行了.

贴上新的询问代码:

int query(int L/*区间[1,l-1]的节点*/,int R/*区间[1,r]的节点*/,int l,int r,int k/*第k小*/){
    if(l==r) return l;
    int mid=(l+r)>>1,sum=t[t[R].l].cnt-t[t[L].l].cnt;//前缀和
    if(sum>=k) return ask(t[L].l,t[R].l,l,mid,k);
    else return ask(t[L].r,t[R].r,mid+1,r,k-sum);
}

到这里,主席树就讲完啦.

上完整代码吧:

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

inline int read(){
    int sum=0,f=1;char c=getchar();
    while(c<'0'||c>'9'){if(c=='-') f=-1;c=getchar();}
    while(c>='0'&&c<='9'){sum=sum*10+c-'0';c=getchar();}
    return sum*f;
}

struct tree{int cnt,l,r;}t[5000001];
int n,m,a[1000001],c[1000001];
int rt[500001],tot=0;

int build(int p,int l,int r,int k){
    int x=++tot;
    t[x]=t[p];t[x].cnt++;
    if(l==r) return x;
    int mid=(l+r)>>1;
    if(k<=mid) t[x].l=build(t[p].l,l,mid,k);
    else t[x].r=build(t[p].r,mid+1,r,k);
    return x;
}

int ask(int L,int R,int l,int r,int k){
    if(l==r) return l;
    int mid=(l+r)>>1,sum=t[t[R].l].cnt-t[t[L].l].cnt;
    if(sum>=k) return ask(t[L].l,t[R].l,l,mid,k);
    else return ask(t[L].r,t[R].r,mid+1,r,k-sum);
}

int main(){
    n=read();m=read();
    for(int i=1;i<=n;i++) a[i]=read();
    memcpy(c,a,sizeof(c));sort(c+1,c+n+1);
    int T=unique(c+1,c+n+1)-c-1;
    for(int i=1;i<=n;i++) a[i]=lower_bound(c+1,c+T+1,a[i])-c;
    for(int i=1;i<=n;i++) rt[i]=build(rt[i-1],1,T,a[i]);
    for(int i=1;i<=m;i++){
        int l=read(),r=read(),k=read();
        printf("%d\n",c[ask(rt[l-1],rt[r],1,T,k)]);
    }
    return 0;
}

以后可能还会更新(埋个坑在这)...

step 3

还真的更新了...

之前,我们讲了可持久化线段树的单点修改对吧.

然而,区间修改去哪了?

但是我们仔细想想,

对于每个版本的线段树,

它们是共用了一些节点,

所以在\(pushdown\) \(tag\)的时候,就会出锅...(自己\(yy\)一下就清楚了)

因此,我们有了一种新的操作——标记永久化.

将一个点的\(tag\)一直存下来,在询问的时候直接加上去.

而在修改的时候,只要被区间覆盖到,就要新建节点.

并且,还要一边切割需要修改的区间(这个等下看代码吧),

一直到完全重合时再返回.

来上修改和查询的代码吧:

int update(int p,int l,int r,int d){
	int x=++tot;t[x]=t[p];
	t[x].sum+=(r-l+1)*d;
	if(t[x].l==l&&t[x].r==r){//完全重合时返回
		t[x].tag+=d;return x;
	}
	int mid=(t[x].l+t[x].r)>>1;
	if(r<=mid) t[x].ls=update(t[p].ls,l,r,d);//把要修改的区间切一下
	else if(l>mid) t[x].rs=update(t[p].rs,l,r,d);
	else t[x].ls=update(t[p].ls,l,mid,d),t[x].rs=update(t[p].rs,mid+1,r,d);
	return x;
}

ll ask(int p,int ad/*一路加上的tag*/,int l,int r){
	if(t[p].l==l&&t[p].r==r){
		return (r-l+1)*ad/*别忘了tag*/+t[p].sum;
	}
	int mid=(t[p].l+t[p].r)>>1;
	if(r<=mid) return ask(t[p].ls,ad+t[p].tag,l,r);
	else if(l>mid) return ask(t[p].rs,ad+t[p].tag,l,r);
	else return ask(t[p].ls,ad+t[p].tag,l,mid)+ask(t[p].rs,ad+t[p].tag,mid+1,r);
}

接下来,让我们来看道例题吧:洛谷SP11470 TTM - To the moon

这题就是标记永久化的板子了.

看代码吧:

#include <iostream>
#include <cstdio>
#include <cstring>
#define ll long long
using namespace std;

inline int read(){
	int sum=0,f=1;char c=getchar();
	while(c<'0'||c>'9'){if(c=='-') f=-1;c=getchar();}
	while(c>='0'&&c<='9'){sum=sum*10+c-'0';c=getchar();}
	return sum*f;
}

struct tree{int l,r,ls,rs;ll sum,tag;}t[2000021];
int n,m,a[500001];
int tt=0,tot=0,rt[500001];

inline void pushup(int p){
	t[p].sum=t[t[p].ls].sum+t[t[p].rs].sum;
}

inline void build(int &p,int l,int r){
	p=++tot;t[p].l=l;t[p].r=r;
	if(l==r){t[p].sum=a[l];return ;}
	int mid=(l+r)>>1;
	build(t[p].ls,l,mid);build(t[p].rs,mid+1,r);
	pushup(p);
}

int update(int p,int l,int r,int d){
	int x=++tot;t[x]=t[p];
	t[x].sum+=(r-l+1)*d;
	if(t[x].l==l&&t[x].r==r){
		t[x].tag+=d;return x;
	}
	int mid=(t[x].l+t[x].r)>>1;
	if(r<=mid) t[x].ls=update(t[p].ls,l,r,d);
	else if(l>mid) t[x].rs=update(t[p].rs,l,r,d);
	else t[x].ls=update(t[p].ls,l,mid,d),t[x].rs=update(t[p].rs,mid+1,r,d);
	return x;
}

ll ask(int p,int ad,int l,int r){
	if(t[p].l==l&&t[p].r==r){
		return (r-l+1)*ad+t[p].sum;
	}
	int mid=(t[p].l+t[p].r)>>1;
	if(r<=mid) return ask(t[p].ls,ad+t[p].tag,l,r);
	else if(l>mid) return ask(t[p].rs,ad+t[p].tag,l,r);
	else return ask(t[p].ls,ad+t[p].tag,l,mid)+ask(t[p].rs,ad+t[p].tag,mid+1,r);
}

inline void change(){
	int l=read(),r=read(),d=read();
	rt[tt+1]=update(rt[tt],l,r,d);tt++;
}

inline void query(int x){
	int l=read(),r=read(),opt=(x? read():tt);
	printf("%lld\n",ask(rt[opt],0,l,r));
}

inline void back(int x){
	tt=x;tot=rt[x+1]-1;
}

int main(){
	n=read();m=read();
	for(int i=1;i<=n;i++) a[i]=read();
	build(rt[0],1,n);
	for(int i=1;i<=m;i++){
		char opt[5];cin>>opt;
		if(opt[0]=='C') change();
		else if(opt[0]=='Q') query(0);
		else if(opt[0]=='H'){query(1);}
		else if(opt[0]=='B'){int x=read();back(x);}
	}
	return 0;
}