BZOJ3907网格

这东西是拿Cat思想搞得组合数学。

首先做这个需要会用网格法或折线法分析Cat的$C_{2n}^n-C_{2n}^{n-1}$是怎么来的。

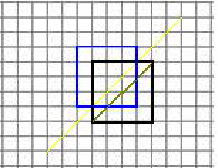
网格法：假如没有限制，从（0，0）到（n，n）的方案数为$C_{2n}^n$，就是一共有2n次操作位置（向右或向上），我们把向上走的操作插入这些位置即得上式，上面的黄线是当我们走到不合法情况时所碰到的第一条线，然后最终我们会走到（n,n）这个点，如果我们将矩形沿着这条线翻折，我们碰到黄线，然后走到（n,n）的走法，可以映射为碰到黄线，然后走到（n-1,n+1）的走法，因为对称嘛。

而我们碰到黄线之前的走法在矩阵翻折中是不受影响的，这样，不合法方案数就是从（0,0）走到（n-1,n+1）的方案数，这个分析和上面差不多，总共$C_{2n}^{n-1}$种，全部的减去不合法的，就是合法的，$C_{2n}^n-C_{2n}^{n-1}$。

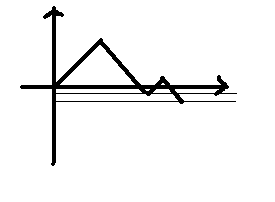
折线法：就是从（0,0）到（2n,0），每次只能沿y=x或y=-x走一个单位，最后图像整体没有位于x下方的部分的方案数。没有限制的话，总方案数为$C_{2n}^n$，因为可以把折线拆成2n段，那么有n段上扬，n段下跌。不能越过x轴，从第一次碰到y=-1这条线开始就不合法了，我们把这个点以后的折线沿y=-1翻折，由于最后到达（2n,0）点，翻折后就到达（2n,-2），此时问题转化为从（0,0）到（2n，-2）的方案数，有n段，n-1段上扬，n+1段下跌，方案数$C_{2n}^{n-1}$，全部的减去不合法的，就是合法的，$C_{2n}^n-C_{2n}^{n-1}$。

那这个题就简单多了，同样用上面的方法，把一个n换成m就差不多了

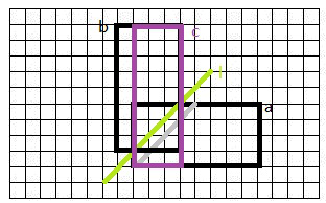
答案就是$C_{n+m}^n-C_{n+m}^{m-1}$，下面的代码是化简后的式子，没有高精减，高精除用唯一分解刚过去，而且时间复杂度也还好，就打的n√n的拆分，n的拆分（我自己证的，可能是假的）在下一篇博客里，（因为那个题√n拆过不去QAQ）。

#include<iostream>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<cstdio>
#include<vector>
#include<queue>
#include<stack>
#include<set>
#include<map>
using namespace std;
int n,m;
int prime[],prime_num;
bool v[];
int fz[],fm[];
struct Bigint{
    int a[],len;
    void clear(){
        memset(a,,sizeof(a));
        a[]=;
        len=;
    }
    friend void operator * (Bigint &x,int y){
        int delta=;
        for(int i=;i<=x.len;i++){
            x.a[i]=x.a[i]*y+delta;
            delta=x.a[i]/;
            x.a[i]%=;
        }
        while(delta>){
            x.a[++x.len]=delta%;
            delta/=;
        }
        while(x.a[x.len]==&&x.len>)
            x.len--;
    }
    void out(){
        for(int i=len;i>=;i--)
            printf("%d",a[i]);
    }
}ans;
void doprime(){
    for(int i=;i<=;i++){
        if(!v[i]) prime[++prime_num]=i;
        for(int j=;j<=prime_num&&i*prime[j]<=;j++){
            v[i*prime[j]]=;
            if(i%prime[j]==) break;
        }
    }
}
void mulfz(int x){
    for(int i=;i<=prime_num;i++)
        while(x%prime[i]==){
            fz[i]++;
            x/=prime[i];
        }
}
void mulfm(int x){
    for(int i=;i<=prime_num;i++)
        while(x%prime[i]==){
            fm[i]++;
            x/=prime[i];
        }
}
int main(){
    scanf("%d%d",&n,&m);
    doprime();ans.clear();
    for(int i=;i<=n+m;i++)
        mulfz(i);
    mulfz(n-m+);
    for(int i=;i<=m;i++)
        mulfm(i);
    for(int i=;i<=n+;i++)
        mulfm(i);
    /*for(int i=1;i<=prime_num;i++)
        cout<<prime[i]<<" ";cout<<endl;*/
    for(int i=;i<=prime_num;i++){
        for(int j=;j<=fz[i]-fm[i];j++)
            ans*prime[i];
    }
    ans.out();
    puts("");
    return ;
}