windwos下的转excel到PDF并预览的工具,有Aspose,Spire,原生Office三种方式
SchacoPDFViewer
项目链接:https://github.com/tiancai4652/SchacoPDFViewer/tree/master
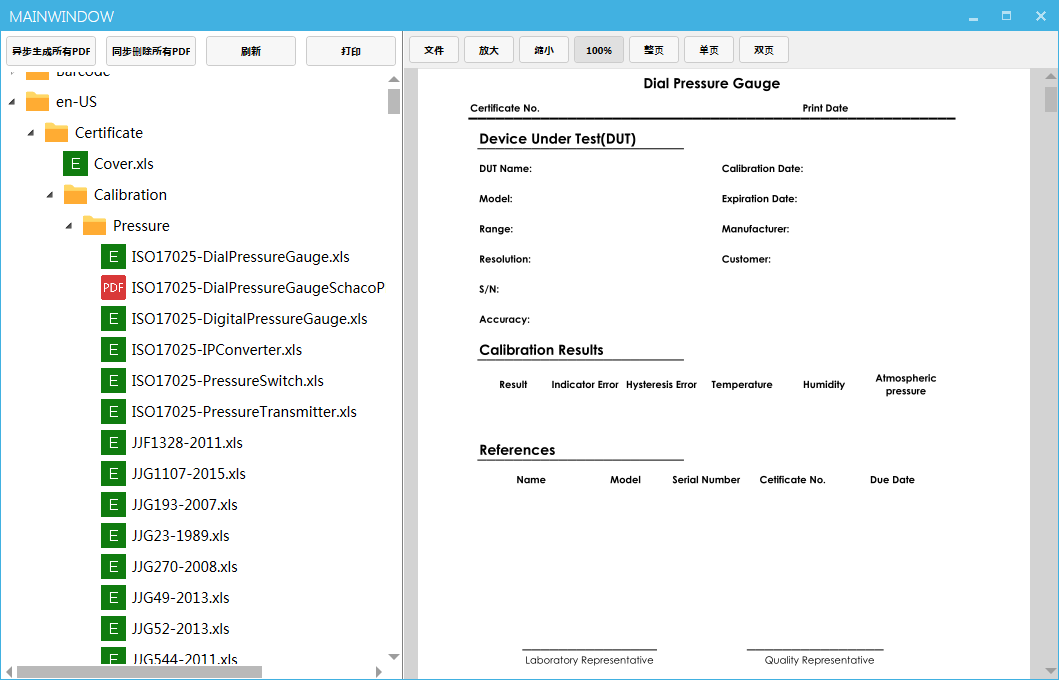
主要实现了对于Excel文件转换PDF,并提供了PDF预览的界面
主要应用的技数:
MahaApp.Metro
MvvmLight
Aspose,Spire,Office操作Excel PDF
libmupdf进行pdf预览
一 操作说明

- 点击...选择包含Excel/Pdf文件的文件夹
- 选择Excel转Pdf组件,包括Aspose库(不需要安装Office),Spire库(不需要安装Office),原生Office库
(需要安装MS Office) - 选择打印PDF工具和打印Excl工具
- 点击Next

- 双击Excel将会将Excel文件转换成PDF文件并输出到界面(每次双击将会重新生成并覆盖上一个PDF文件),双击PDF文件将会将其输出到界面
本工具制作用途
为了解决通过原生Office转excel到PDF的用户必须安装MS Office才能转换,进而测试不依赖Office的组件Aspose和Spire
再次吐槽一下客户Office的坑
1 客户是精简版Office
2 Office2007还需要安装XPS组件
3 客户用不同版本的Office编辑Excel有兼容性错误
4 Win10自带的Office需要重新安装才能转POF(即不是完整安装)
windwos下的转excel到PDF并预览的工具,有Aspose,Spire,原生Office三种方式的更多相关文章
- 基于DevExpress实现对PDF、Word、Excel文档的预览及操作处理
http://www.cnblogs.com/wuhuacong/p/4175266.html 在一般的管理系统模块里面,越来越多的设计到一些常用文档的上传保存操作,其中如PDF.Word.Excel ...
- Aspose office (Excel,Word,PPT),PDF 在线预览
前文: 做个备份,拿的是试用版的 Aspose,功能见标题 代码: /// <summary> /// Aspose office (Excel,Word,PPT),PDF 在线预览 // ...
- 实战动态PDF在线预览及带签名的PDF文件转换
开篇语: 最近工作需要做一个借款合同,公司以前的合同都是通过app端下载,然后通过本地打开pdf文件,而喜欢创新的我,心想着为什么不能在线H5预览,正是这个想法,说干就干,实践过程总是艰难的,折腾了3 ...
- Office在线预览及PDF在线预览的实现方式史上最全大集合
Office在线预览及PDF在线预览的实现方式大集合 一.服务器先转换为PDF,再转换为SWF,最后通过网页加载Flash预览 微软方:利用Office2007以上版本的一个PDF插件SaveAsPD ...
- 动态PDF在线预览
实战动态PDF在线预览及带签名的PDF文件转换 开篇语: 最近工作需要做一个借款合同,公司以前的合同都是通过app端下载,然后通过本地打开pdf文件,而喜欢创新的我,心想着为什么不能在线H5预览,正是 ...
- 【整理】Linux下中文检索引擎coreseek4安装,以及PHP使用sphinx的三种方式(sphinxapi,sphinx的php扩展,SphinxSe作为mysql存储引擎)
一,软件准备 coreseek4.1 (包含coreseek测试版和mmseg最新版本,以及测试数据包[内置中文分词与搜索.单字切分.mysql数据源.python数据源.RT实时索引等测 ...
- 在Tomcat下部属项目三种方式:
在Tomcat下部属项目三种方式: 1直接复制: 2. 通过配置虚拟路径的方式 直接修改配置文件 写到tomcat/conf/server.xml 找到<H ...
- 启动bash shell的三种方式下,检查的启动文件
启动bash shell的三种方式 1.登录时当做默认登录shell 2.作为非登录shell的交互式shell 3.作为运行脚本的非交互shell 一.登录shell 登录Linux系统时,bash ...
- Python|读、写Excel文件(三种模块三种方式)
python读写excel的方式有很多,不同的模块在读写的讲法上稍有区别: 用xlrd和xlwt进行excel读写: 用openpyxl进行excel读写: 用pandas进行excel读写: imp ...
随机推荐
- 拯救 Out Of Memory,8个案例带你飞!
来自:唐尤华 https://bloggceasy.files.wordpress.com/2015/05/outofmemoryerror2.pdf 1. Java 堆空间 发生频率:5颗星 造成原 ...
- 豆瓣图书Top250
从豆瓣图书Top250抓取数据,并通过词云图展示 导入库 from lxml import etree #解析库 import time #时间 import random #随机函数 import ...
- CSS 案例学习
1.样式 display:inline-block;可改变a标签,合其可定义宽高 2.a:hover表示鼠标经过 3.background:url(110.png) bottom 表示:给链接一个图片 ...
- 3-Windows-CMD启动mysql服务-连接本地mysql服务-连接远程mysql服务
转自: https://jingyan.baidu.com/article/84b4f565b77a5660f6da32d4.html 备注: 如果在连接远程mysql服务,无法连接时,可能是远程my ...
- 字节流read方法返回值为什么是int不是byte
01001000 01001000 01001000 11111111 01001000 -1的原码: 10000001 -1的反码: 11111110 -1的补码: 11111111 所以如果返回值 ...
- 分布式版本控制工具Mercurial------Linux下hg命令的使用
1.关于hg命令选项: 每一个每一个命令选项都有一个长的名称,如hg log 命令会使用 –rev选项; 大多数选项拥有一个短的名称,如—rev有一个-r的短名: 长名称以两条横线(–)作为起始,短名 ...
- jQuery实现全选与全部选
为了便于用户理解,直接粘贴下面的代码即可 <!DOCTYPE html> <html lang="en"> <head> <meta ch ...
- java内省Introspector
大纲: JavaBean 规范 内省 一.JavaBean 规范 JavaBean —般需遵循以下规范. 实现 java.io.Serializable 接口. javaBean属性是具有getter ...
- 【转载】WebRTC基于GCC的拥塞控制(上) - 算法分析
实时流媒体应用的最大特点是实时性,而延迟是实时性的最大敌人.从媒体收发端来讲,媒体数据的处理速度是造成延迟的重要原因:而从传输角度来讲,网络拥塞则是造成延迟的最主要原因.网络拥塞可能造成数据包丢失,也 ...
- 01二维背包——poj2576
/* 要求把a数组分成两个集合,两个集合人数最多差1,并且元素之和的差尽可能小 那只要把所有可行的列出来即可 01二维背包,即体积是个二维数据,那么我们的背包状态也应该设为二维 dp[j][k]设为 ...
