压缩感知重构算法之子空间追踪(SP)



function [ theta ] = CS_SP( y,A,K )
%CS_SP Summary of this function goes here
%Version: 1.0 written by jbb0523 @2015-05-01
% Detailed explanation goes here
% y = Phi * x
% x = Psi * theta
% y = Phi*Psi * theta
% 令 A = Phi*Psi, 则y=A*theta
% K is the sparsity level
% 现在已知y和A,求theta
% Reference:Dai W,Milenkovic O.Subspace pursuit for compressive sensing
% signal reconstruction[J].IEEE Transactions on Information Theory,
% 2009,55(5):2230-2249.
[y_rows,y_columns] = size(y);
if y_rows<y_columns
y = y';%y should be a column vector
end
[M,N] = size(A);%传感矩阵A为M*N矩阵
theta = zeros(N,1);%用来存储恢复的theta(列向量)
Pos_theta = [];%用来迭代过程中存储A被选择的列序号
r_n = y;%初始化残差(residual)为y
for kk=1:K%最多迭代K次
%(1) Identification
product = A'*r_n;%传感矩阵A各列与残差的内积
[val,pos]=sort(abs(product),'descend');
Js = pos(1:K);%选出内积值最大的K列
%(2) Support Merger
Is = union(Pos_theta,Js);%Pos_theta与Js并集
%(3) Estimation
%At的行数要大于列数,此为最小二乘的基础(列线性无关)
if length(Is)<=M
At = A(:,Is);%将A的这几列组成矩阵At
else%At的列数大于行数,列必为线性相关的,At'*At将不可逆
break;%跳出for循环
end
%y=At*theta,以下求theta的最小二乘解(Least Square)
theta_ls = (At'*At)^(-1)*At'*y;%最小二乘解
%(4) Pruning
[val,pos]=sort(abs(theta_ls),'descend');
%(5) Sample Update
Pos_theta = Is(pos(1:K));
theta_ls = theta_ls(pos(1:K));
%At(:,pos(1:K))*theta_ls是y在At(:,pos(1:K))列空间上的正交投影
r_n = y - At(:,pos(1:K))*theta_ls;%更新残差
if norm(r_n)<1e-6%Repeat the steps until r=0
break;%跳出for循环
end
end
theta(Pos_theta)=theta_ls;%恢复出的theta
end
clear all;close all;clc;
load CoSaMPMtoPercentage1000;
PercentageCoSaMP = Percentage;
load SPMtoPercentage1000;
PercentageSP = Percentage;
S1 = ['-ks';'-ko';'-kd';'-kv';'-k*'];
S2 = ['-rs';'-ro';'-rd';'-rv';'-r*'];
figure;
for kk = 1:length(K_set)
K = K_set(kk);
M_set = 2*K:5:N;
L_Mset = length(M_set);
plot(M_set,PercentageCoSaMP(kk,1:L_Mset),S1(kk,:));%绘出x的恢复信号
hold on;
plot(M_set,PercentageSP(kk,1:L_Mset),S2(kk,:));%绘出x的恢复信号
end
hold off;
xlim([0 256]);
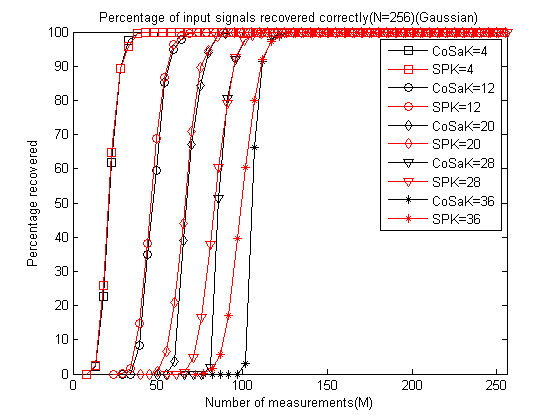
legend('CoSaK=4','SPK=4','CoSaK=12','SPK=12','CoSaK=20',...
'SPK=20','CoSaK=28','SPK=28','CoSaK=36','SPK=36');
xlabel('Number of measurements(M)');
ylabel('Percentage recovered');
title('Percentage of input signals recovered correctly(N=256)(Gaussian)');

压缩感知重构算法之子空间追踪(SP)的更多相关文章
- 浅谈压缩感知(二十四):压缩感知重构算法之子空间追踪(SP)
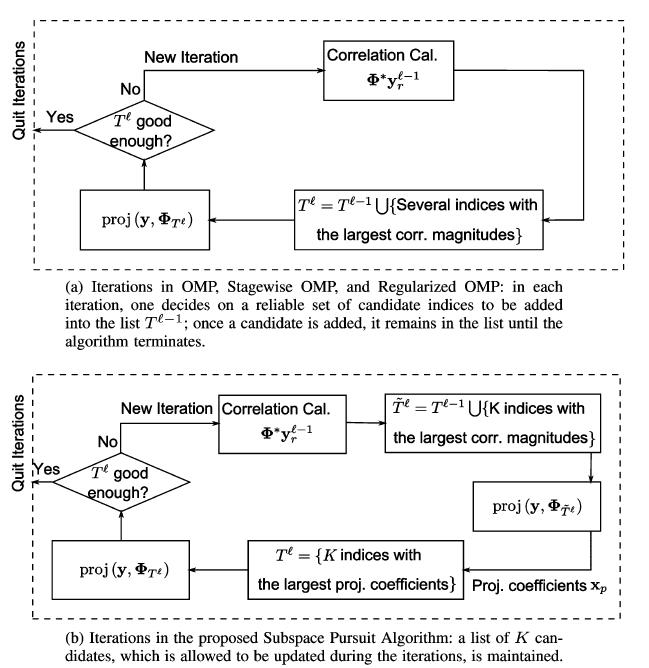
主要内容: SP的算法流程 SP的MATLAB实现 一维信号的实验与结果 测量数M与重构成功概率关系的实验与结果 SP与CoSaMP的性能比较 一.SP的算法流程 压缩采样匹配追踪(CoSaMP)与子 ...
- 浅谈压缩感知(二十八):压缩感知重构算法之广义正交匹配追踪(gOMP)
主要内容: gOMP的算法流程 gOMP的MATLAB实现 一维信号的实验与结果 稀疏度K与重构成功概率关系的实验与结果 一.gOMP的算法流程 广义正交匹配追踪(Generalized OMP, g ...
- 浅谈压缩感知(二十五):压缩感知重构算法之分段正交匹配追踪(StOMP)
主要内容: StOMP的算法流程 StOMP的MATLAB实现 一维信号的实验与结果 门限参数Ts.测量数M与重构成功概率关系的实验与结果 一.StOMP的算法流程 分段正交匹配追踪(Stagewis ...
- 浅谈压缩感知(二十六):压缩感知重构算法之分段弱正交匹配追踪(SWOMP)
主要内容: SWOMP的算法流程 SWOMP的MATLAB实现 一维信号的实验与结果 门限参数a.测量数M与重构成功概率关系的实验与结果 SWOMP与StOMP性能比较 一.SWOMP的算法流程 分段 ...
- 压缩感知重构算法之压缩采样匹配追踪(CoSaMP)
压缩采样匹配追踪(CompressiveSampling MP)是D. Needell继ROMP之后提出的又一个具有较大影响力的重构算法.CoSaMP也是对OMP的一种改进,每次迭代选择多个原子,除了 ...
- [转]压缩感知重构算法之分段正交匹配追踪(StOMP)
分段正交匹配追踪(StagewiseOMP)或者翻译为逐步正交匹配追踪,它是OMP另一种改进算法,每次迭代可以选择多个原子.此算法的输入参数中没有信号稀疏度K,因此相比于ROMP及CoSaMP有独到的 ...
- 浅谈压缩感知(二十三):压缩感知重构算法之压缩采样匹配追踪(CoSaMP)
主要内容: CoSaMP的算法流程 CoSaMP的MATLAB实现 一维信号的实验与结果 测量数M与重构成功概率关系的实验与结果 一.CoSaMP的算法流程 压缩采样匹配追踪(CompressiveS ...
- 浅谈压缩感知(二十二):压缩感知重构算法之正则化正交匹配追踪(ROMP)
主要内容: ROMP的算法流程 ROMP的MATLAB实现 一维信号的实验与结果 测量数M与重构成功概率关系的实验与结果 一.ROMP的算法流程 正则化正交匹配追踪ROMP算法流程与OMP的最大不同之 ...
- 浅谈压缩感知(二十一):压缩感知重构算法之正交匹配追踪(OMP)
主要内容: OMP的算法流程 OMP的MATLAB实现 一维信号的实验与结果 测量数M与重构成功概率关系的实验与结果 稀疏度K与重构成功概率关系的实验与结果 一.OMP的算法流程 二.OMP的MATL ...
随机推荐
- Java数据库连接泄漏应对办法-基于Weblogic服务器
临时解决连接泄漏方案 当连接泄漏真的发生了,无可避免时,我们采取以下方案,可临时解决连接问题,以争取修改代码的时间. 步骤1:选择待分析的JNDI数据源 步骤2(可选):可配置最大数据连接数量 步骤3 ...
- Oracle存储过程经典入门
ok基本就这些介绍
- centOS 6 服务管理与服务脚本
服务管理与服务脚本 linux服务 服务管理与服务脚本 linux服务 服务启动过程详解 chkconfig命令 非独立服务与xinetd进程 一个特殊的服务脚本 服务启动过程详解 在开机启动 ...
- OpenStack Ocata 超详细搭建文档
前言 搭建前必须看我本文档搭建的是分布式O版openstack(controller+ N compute + 1 cinder)的文档.openstack版本为Ocata.搭建的时候,请严格按照文档 ...
- 关于ng-options
在实际使用过程中对angular的ng-options指令有点不解,有的时候觉得很容易理解和上手,但其实等到遇到问题时,发现它很是生疏,(key,value)键值对获取,as关键词,track by ...
- [AHOI2001]彩票摇奖
[AHOI2001]彩票摇奖 题目描述 为了丰富人民群众的生活.支持某些社会公益事业,北塔市设置了一 项彩票.该彩票的规则是: (1) 每张彩票上印有 7 个各不相同的号码,且这些号码的取指范围为 1 ...
- BZOJ1207_打鼹鼠_KEY
[HNOI2004]打鼹鼠 Time Limit: 10 Sec Memory Limit: 162 MB Description 鼹鼠是一种很喜欢挖洞的动物,但每过一定的时间,它还是喜欢把头探出到地 ...
- 混合高斯模型(Mixtures of Gaussians)和EM算法
这篇讨论使用期望最大化算法(Expectation-Maximization)来进行密度估计(density estimation). 与k-means一样,给定的训练样本是,我们将隐含类别标签用表示 ...
- Python3常用学习网站总结(随时更新)
Python资源大全 http://python.jobbole.com/84464/ https://github.com/jobbole/awesome-python-cn scrapy: h ...
- WPF---Effect效果
在 WPF 中,可以使用 BitmapEffect 对象为每一个 Visual 对象生成各种各样的效果,一个 Visual 对象可以设置一种或多种 BitmapEffect 效果,WPF 内置了几种效 ...
