机器学习公开课笔记(4)：神经网络(Neural Network)—

动机(Motivation)

对于非线性分类问题，如果用多元线性回归进行分类，需要构造许多高次项，导致特征特多学习参数过多，从而复杂度太高。

神经网络(Neural Network)

一个简单的神经网络如下图所示，每一个圆圈表示一个神经元，每个神经元接收上一层神经元的输出作为其输入，同时其输出信号到下一层，其中每一层的第一个神经元称为bias unit，它是额外加入的其值为1，通常用+1表示,下图用虚线画出。

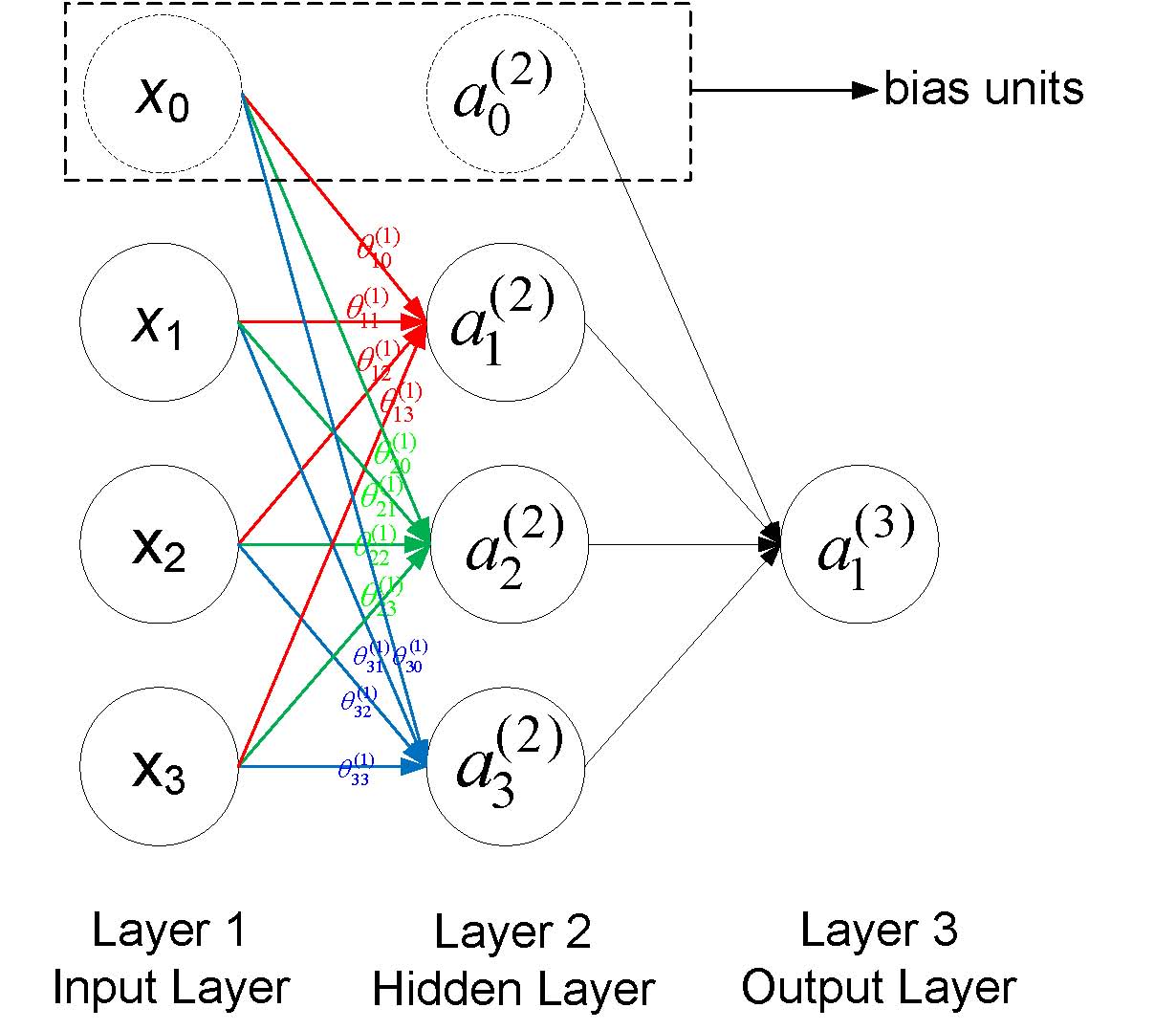
符号说明：

$a_i^{(j)}$表示第j层网络的第i个神经元，例如下图$a_1^{(2)}$就表示第二层的第一个神经元
$\theta^{(j)}$表示从第$j$层到第$j+1$层的权重矩阵，例如下图所有的$\theta^{(1)}$表示从第一层到第二层的权重矩阵
$\theta^{(j)}_{uv}$表示从第j层的第v个神经元到第j+1层的第u个神经的权重，例如下图中$\theta^{(1)}_{23}$表示从第一层的第3个神经元到第二层的第2个神经元的权重，需要注意到的是下标uv是指v->u的权重而不是u->v，下图也给出了第一层到第二层的所有权重标注
一般地，如果第j层有$s_j$个神经元（不包括bias神经元），第j+1层有$s_{j+1}$个神经元（也不包括bias神经元），那么权重矩阵$\theta^{j}$的维度是$(s_{j+1}\times s_j+1)$

前向传播(Forward Propagration, FP)

后一层的神经元的值根据前一层神经元的值的改变而改变，以上图为例，第二层的神经元的更新方式为

$$a_1^{(2)} = g(\theta_{10}^{(1)}x_0 + \theta_{11}^{(1)}x_1 + \theta_{12}^{(1)}x_2 + \theta_{13}^{(1)}x_3)$$

$$a_2^{(2)} = g(\theta_{20}^{(1)}x_0 + \theta_{21}^{(1)}x_1 + \theta_{22}^{(1)}x_2 + \theta_{23}^{(1)}x_3)$$

$$a_3^{(2)} = g(\theta_{30}^{(1)}x_0 + \theta_{31}^{(1)}x_1 + \theta_{32}^{(1)}x_2 + \theta_{33}^{(1)}x_3)$$

$$a_4^{(2)} = g(\theta_{40}^{(1)}x_0 + \theta_{41}^{(1)}x_1 + \theta_{42}^{(1)}x_2 + \theta_{43}^{(1)}x_3)$$

其中g(z)为sigmoid函数，即$g(z)=\frac{1}{1+e^{-z}}$

1. 向量化实现(Vectorized Implementation)

如果我们以向量角度来看待上述的更新公式，定义

$a^{(1)}=x=\left[ \begin{matrix}x_0\\ x_1 \\ x_2 \\ x_3 \end{matrix} \right]$ $z^{(2)}=\left[ \begin{matrix}z_1^{(2)}\\ z_1^{(2)} \\ z_1^{(2)}\end{matrix} \right]$ $\theta^{(1)}=\left[\begin{matrix}\theta^{(1)}_{10}& \theta^{(1)}_{11}& \theta^{(1)}_{12}& \theta^{(1)}_{13}\\ \theta^{(1)}_{20}& \theta^{(1)}_{21}& \theta^{(1)}_{22}& \theta^{(1)}_{23}\\ \theta^{(1)}_{30}& \theta^{(1)}_{31}& \theta^{(1)}_{32} & \theta^{(1)}_{33}\end{matrix}\right]$

则更新公式可以简化为

$$z^{(2)}=\theta^{(1)}a^{(1)}$$

$$a^{(2)}=g(z^{(2)})$$

$$z^{(3)}=\theta^{(2)}a^{(2)}$$

$$a^{(3)}=g(z^{(3)})=h_\theta(x)$$

可以看到，我们由第一层的值，计算第二层的值；由第二层的值，计算第三层的值，得到预测的输出，计算的方式一层一层往前走的，这也是前向传播的名称由来。

2. 与Logistic回归的联系

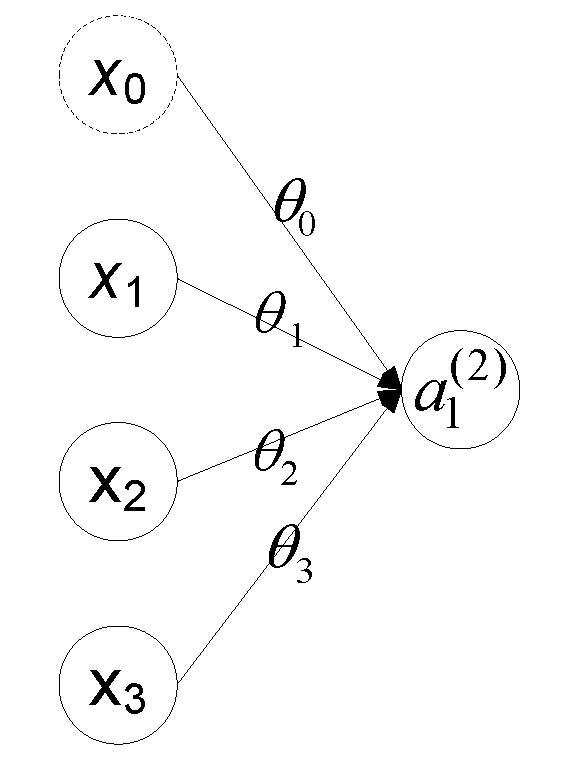
考虑上图没有隐藏层的神经网络，其中$x=\left[ \begin{matrix}x_0\\ x_1 \\ x_2 \\ x_3 \end{matrix} \right]$，$\theta=\left[ \begin{matrix}\theta_0& \theta_1& \theta_2 & \theta_3 \end{matrix} \right]$，则我们有$h_\theta(x)=a_1^{(2)}=g(z^{(1)})=g(\theta x)=g(x_0\theta_0+x_1\theta_1+x_2\theta_2+x_3\theta_3)$，可以看到这正是Logistic回归的假设函数！！！这种关系表明Logistic是回归是不含隐藏层的特殊神经网络，神经网络从某种程度上来说是对logistic回归的推广。

神经网络示例

对于如下图所示的线性不可分的分类问题，(0,0)(1,1)为一类(0,1)(1,0)为另一类，神经网络可以解决（见5）。首先需要一些简单的神经网络(1-4)，其中图和真值表结合可以清楚的看出其功能，不再赘述。

1. 实现AND操作

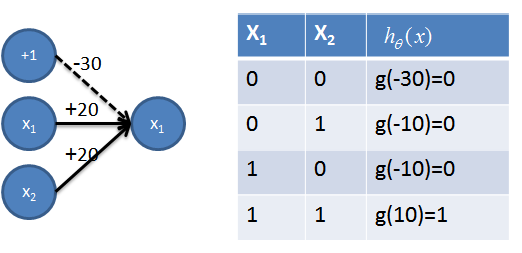
2. 实现OR操作

3. 实现非操作

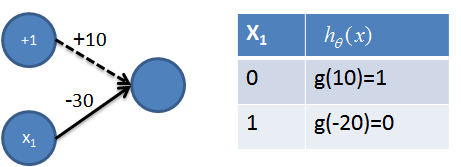
4. 实现NAND=((not x1) and (not x2))操作

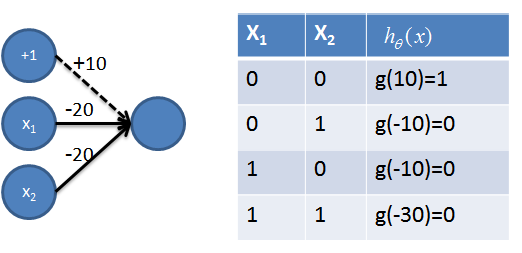
5. 组合实现NXOR=NOT(x1 XOR x2) 操作

该神经网络用到了之前的AND操作（用红色表示）、NAND操作（用青色表示）和OR操作（用橙色表示），从真值表可以看出，该神经网络成功地将(0, 0)(1,1)分为一类，(1,0)(0,1)分为一类，很好解决了线性不可分的问题。

神经网络的代价函数(含正则项)

$$J(\Theta) = -\frac{1}{m}\left[\sum\limits_{i=1}^{m}\sum\limits_{k=1}^{K}y^{(i)}_{k}log(h_\theta(x^{(i)}))_k + (1-y^{(i)}_k)log(1-(h_\theta(x^{(i)}))_k)\right] + \frac{\lambda}{2m}\sum_{l=1}^{L-1}\sum\limits_{i=1}^{s_l}\sum\limits_{j=1}^{s_{l+1}}(\Theta_{ji}^{(l)})^2$$

符号说明：

$m$ — 训练example的数量
$K$ — 最后一层（输出层）的神经元的个数，也等于分类数（分$K$类，$K\geq 3$）
$y_k^{(i)}$ — 第$i$个训练exmaple的输出(长度为$K$个向量)的第$k$个分量值
$(h_\theta(x^{(i)}))_k$ — 对第$i$个example用神经网络预测的输出(长度为$K$的向量)的第$k$个分量值
$L$ — 神经网络总共的层数（包括输入层和输出层）
$\Theta^{(l)}$ — 第$l$层到第$l+1$层的权重矩阵
$s_l$ — 第$l$层神经元的个数, 注意$i$从1开始计数，bias神经元的权重不算在正则项内
$s_{l+1}$ — 第$l+1$ 层神经元的个数

参考文献

[1] Andrew Ng Coursera 公开课第四周

[2] Neural Networks. https://www.doc.ic.ac.uk/~nd/surprise_96/journal/vol4/cs11/report.html

[3] The nature of code. http://natureofcode.com/book/chapter-10-neural-networks/

[4] A Basic Introduction To Neural Networks. http://pages.cs.wisc.edu/~bolo/shipyard/neural/local.html