二叉堆(二)之 C++的实现
概要
上一章介绍了堆和二叉堆的基本概念,并通过C语言实现了二叉堆。本章是二叉堆的C++实现。
目录
1. 二叉堆的介绍
2. 二叉堆的图文解析
3. 二叉堆的C++实现(完整源码)
4. 二叉堆的C++测试程序
转载请注明出处:http://www.cnblogs.com/skywang12345/p/3610382.html
更多内容:数据结构与算法系列 目录
(01) 二叉堆(一)之 图文解析 和 C语言的实现
(02) 二叉堆(二)之 C++的实现
(03) 二叉堆(三)之 Java的实
二叉堆的介绍
二叉堆是完全二元树或者是近似完全二元树,按照数据的排列方式可以分为两种:最大堆和最小堆。
最大堆:父结点的键值总是大于或等于任何一个子节点的键值;最小堆:父结点的键值总是小于或等于任何一个子节点的键值。示意图如下:

二叉堆一般都通过"数组"来实现。数组实现的二叉堆,父节点和子节点的位置存在一定的关系。有时候,我们将"二叉堆的第一个元素"放在数组索引0的位置,有时候放在1的位置。当然,它们的本质一样(都是二叉堆),只是实现上稍微有一丁点区别。
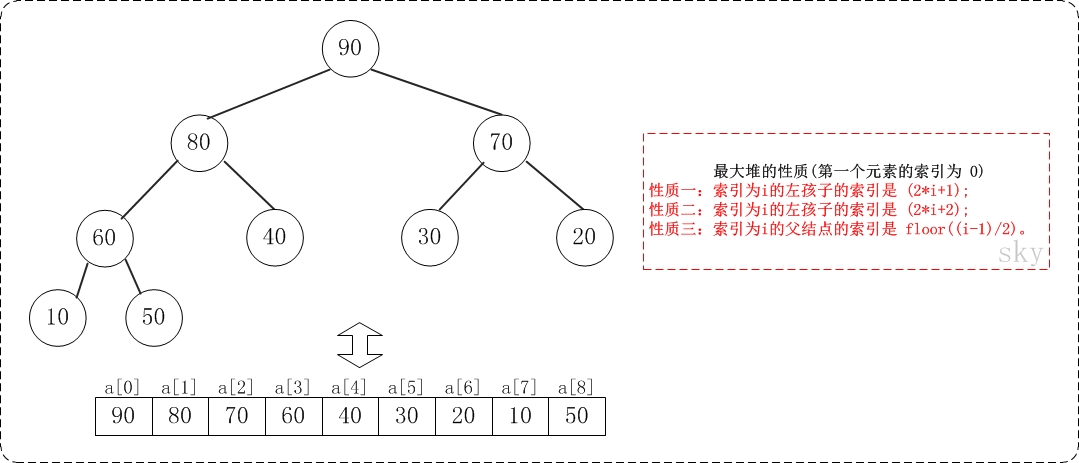
假设"第一个元素"在数组中的索引为 0 的话,则父节点和子节点的位置关系如下:
(01) 索引为i的左孩子的索引是 (2*i+1);
(02) 索引为i的左孩子的索引是 (2*i+2);
(03) 索引为i的父结点的索引是 floor((i-1)/2);
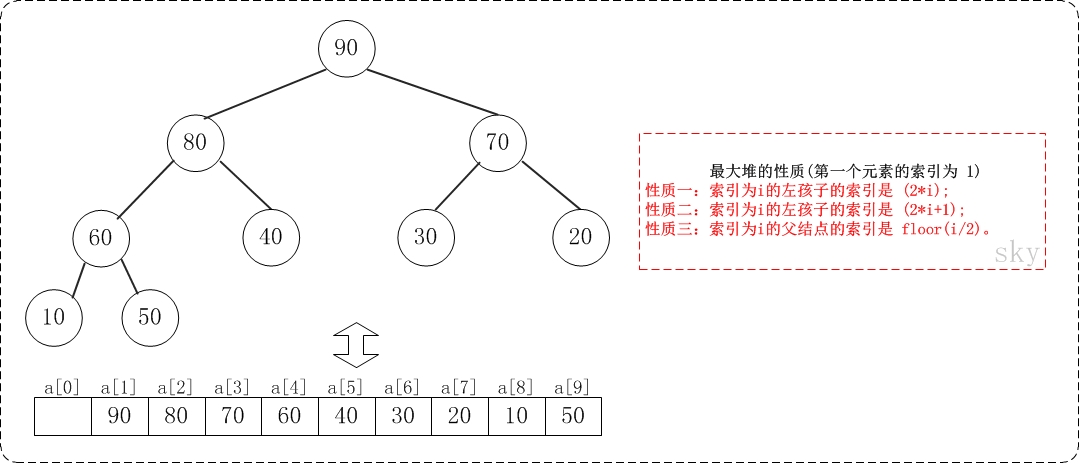
假设"第一个元素"在数组中的索引为 1 的话,则父节点和子节点的位置关系如下:
(01) 索引为i的左孩子的索引是 (2*i);
(02) 索引为i的左孩子的索引是 (2*i+1);
(03) 索引为i的父结点的索引是 floor(i/2);
注意:本文二叉堆的实现统统都是采用"二叉堆第一个元素在数组索引为0"的方式!
二叉堆的图文解析
图文解析是以"最大堆"来进行介绍的。
1. 基本定义
template <class T>
class MaxHeap{
private:
T *mHeap; // 数据
int mCapacity; // 总的容量
int mSize; // 实际容量 private:
// 最大堆的向下调整算法
void filterdown(int start, int end);
// 最大堆的向上调整算法(从start开始向上直到0,调整堆)
void filterup(int start);
public:
MaxHeap();
MaxHeap(int capacity);
~MaxHeap(); // 返回data在二叉堆中的索引
int getIndex(T data);
// 删除最大堆中的data
int remove(T data);
// 将data插入到二叉堆中
int insert(T data);
// 打印二叉堆
void print();
};
MaxHeap是最大堆的对应的类。它包括的核心内容是"添加"和"删除",理解这两个算法,二叉堆也就基本掌握了。下面对它们进行介绍。
2. 添加
假设在最大堆[90,80,70,60,40,30,20,10,50]种添加85,需要执行的步骤如下:

如上图所示,当向最大堆中添加数据时:先将数据加入到最大堆的最后,然后尽可能把这个元素往上挪,直到挪不动为止!
将85添加到[90,80,70,60,40,30,20,10,50]中后,最大堆变成了[90,85,70,60,80,30,20,10,50,40]。
最大堆的插入代码(C++语言)
/*
* 最大堆的向上调整算法(从start开始向上直到0,调整堆)
*
* 注:数组实现的堆中,第N个节点的左孩子的索引值是(2N+1),右孩子的索引是(2N+2)。
*
* 参数说明:
* start -- 被上调节点的起始位置(一般为数组中最后一个元素的索引)
*/
template <class T>
void MaxHeap<T>::filterup(int start)
{
int c = start; // 当前节点(current)的位置
int p = (c-)/; // 父(parent)结点的位置
T tmp = mHeap[c]; // 当前节点(current)的大小 while(c > )
{
if(mHeap[p] >= tmp)
break;
else
{
mHeap[c] = mHeap[p];
c = p;
p = (p-)/;
}
}
mHeap[c] = tmp;
} /*
* 将data插入到二叉堆中
*
* 返回值:
* 0,表示成功
* -1,表示失败
*/
template <class T>
int MaxHeap<T>::insert(T data)
{
// 如果"堆"已满,则返回
if(mSize == mCapacity)
return -; mHeap[mSize] = data; // 将"数组"插在表尾
filterup(mSize); // 向上调整堆
mSize++; // 堆的实际容量+1 return ;
}
insert(data)的作用:将数据data添加到最大堆中。当堆已满的时候,添加失败;否则data添加到最大堆的末尾。然后通过上调算法重新调整数组,使之重新成为最大堆。
3. 删除
假设从最大堆[90,85,70,60,80,30,20,10,50,40]中删除90,需要执行的步骤如下:

如上图所示,当从最大堆中删除数据时:先删除该数据,然后用最大堆中最后一个的元素插入这个空位;接着,把这个“空位”尽量往上挪,直到剩余的数据变成一个最大堆。
从[90,85,70,60,80,30,20,10,50,40]删除90之后,最大堆变成了[85,80,70,60,40,30,20,10,50]。
注意:考虑从最大堆[90,85,70,60,80,30,20,10,50,40]中删除60,执行的步骤不能单纯的用它的字节点来替换;而必须考虑到"替换后的树仍然要是最大堆"!

最大堆的删除代码(C++语言)
/*
* 最大堆的向下调整算法
*
* 注:数组实现的堆中,第N个节点的左孩子的索引值是(2N+1),右孩子的索引是(2N+2)。
*
* 参数说明:
* start -- 被下调节点的起始位置(一般为0,表示从第1个开始)
* end -- 截至范围(一般为数组中最后一个元素的索引)
*/
template <class T>
void MaxHeap<T>::filterdown(int start, int end)
{
int c = start; // 当前(current)节点的位置
int l = *c + ; // 左(left)孩子的位置
T tmp = mHeap[c]; // 当前(current)节点的大小 while(l <= end)
{
// "l"是左孩子,"l+1"是右孩子
if(l < end && mHeap[l] < mHeap[l+])
l++; // 左右两孩子中选择较大者,即mHeap[l+1]
if(tmp >= mHeap[l])
break; //调整结束
else
{
mHeap[c] = mHeap[l];
c = l;
l = *l + ;
}
}
mHeap[c] = tmp;
} /*
* 删除最大堆中的data
*
* 返回值:
* 0,成功
* -1,失败
*/
template <class T>
int MaxHeap<T>::remove(T data)
{
int index;
// 如果"堆"已空,则返回-1
if(mSize == )
return -; // 获取data在数组中的索引
index = getIndex(data);
if (index==-)
return -; mHeap[index] = mHeap[--mSize]; // 用最后元素填补
filterdown(index, mSize-); // 从index位置开始自上向下调整为最大堆 return ;
}
二叉堆的C++实现(完整源码)
二叉堆的实现同时包含了"最大堆"和"最小堆"。
二叉堆(最大堆)的实现文件(MaxHeap.cpp)
/**
* 二叉堆(最大堆)
*
* @author skywang
* @date 2014/03/07
*/ #include <iomanip>
#include <iostream>
using namespace std; template <class T>
class MaxHeap{
private:
T *mHeap; // 数据
int mCapacity; // 总的容量
int mSize; // 实际容量 private:
// 最大堆的向下调整算法
void filterdown(int start, int end);
// 最大堆的向上调整算法(从start开始向上直到0,调整堆)
void filterup(int start);
public:
MaxHeap();
MaxHeap(int capacity);
~MaxHeap(); // 返回data在二叉堆中的索引
int getIndex(T data);
// 删除最大堆中的data
int remove(T data);
// 将data插入到二叉堆中
int insert(T data);
// 打印二叉堆
void print();
}; /*
* 构造函数
*/
template <class T>
MaxHeap<T>::MaxHeap()
{
new (this)MaxHeap();
} template <class T>
MaxHeap<T>::MaxHeap(int capacity)
{
mSize = ;
mCapacity = capacity;
mHeap = new T[mCapacity];
}
/*
* 析构函数
*/
template <class T>
MaxHeap<T>::~MaxHeap()
{
mSize = ;
mCapacity = ;
delete[] mHeap;
} /*
* 返回data在二叉堆中的索引
*
* 返回值:
* 存在 -- 返回data在数组中的索引
* 不存在 -- -1
*/
template <class T>
int MaxHeap<T>::getIndex(T data)
{
for(int i=; i<mSize; i++)
if (data==mHeap[i])
return i; return -;
} /*
* 最大堆的向下调整算法
*
* 注:数组实现的堆中,第N个节点的左孩子的索引值是(2N+1),右孩子的索引是(2N+2)。
*
* 参数说明:
* start -- 被下调节点的起始位置(一般为0,表示从第1个开始)
* end -- 截至范围(一般为数组中最后一个元素的索引)
*/
template <class T>
void MaxHeap<T>::filterdown(int start, int end)
{
int c = start; // 当前(current)节点的位置
int l = *c + ; // 左(left)孩子的位置
T tmp = mHeap[c]; // 当前(current)节点的大小 while(l <= end)
{
// "l"是左孩子,"l+1"是右孩子
if(l < end && mHeap[l] < mHeap[l+])
l++; // 左右两孩子中选择较大者,即mHeap[l+1]
if(tmp >= mHeap[l])
break; //调整结束
else
{
mHeap[c] = mHeap[l];
c = l;
l = *l + ;
}
}
mHeap[c] = tmp;
} /*
* 删除最大堆中的data
*
* 返回值:
* 0,成功
* -1,失败
*/
template <class T>
int MaxHeap<T>::remove(T data)
{
int index;
// 如果"堆"已空,则返回-1
if(mSize == )
return -; // 获取data在数组中的索引
index = getIndex(data);
if (index==-)
return -; mHeap[index] = mHeap[--mSize]; // 用最后元素填补
filterdown(index, mSize-); // 从index位置开始自上向下调整为最大堆 return ;
} /*
* 最大堆的向上调整算法(从start开始向上直到0,调整堆)
*
* 注:数组实现的堆中,第N个节点的左孩子的索引值是(2N+1),右孩子的索引是(2N+2)。
*
* 参数说明:
* start -- 被上调节点的起始位置(一般为数组中最后一个元素的索引)
*/
template <class T>
void MaxHeap<T>::filterup(int start)
{
int c = start; // 当前节点(current)的位置
int p = (c-)/; // 父(parent)结点的位置
T tmp = mHeap[c]; // 当前节点(current)的大小 while(c > )
{
if(mHeap[p] >= tmp)
break;
else
{
mHeap[c] = mHeap[p];
c = p;
p = (p-)/;
}
}
mHeap[c] = tmp;
} /*
* 将data插入到二叉堆中
*
* 返回值:
* 0,表示成功
* -1,表示失败
*/
template <class T>
int MaxHeap<T>::insert(T data)
{
// 如果"堆"已满,则返回
if(mSize == mCapacity)
return -; mHeap[mSize] = data; // 将"数组"插在表尾
filterup(mSize); // 向上调整堆
mSize++; // 堆的实际容量+1 return ;
} /*
* 打印二叉堆
*
* 返回值:
* 0,表示成功
* -1,表示失败
*/
template <class T>
void MaxHeap<T>::print()
{
for (int i=; i<mSize; i++)
cout << mHeap[i] << " ";
} int main()
{
int a[] = {, , , , , , , , };
int i, len=(sizeof(a)) / (sizeof(a[])) ;
MaxHeap<int>* tree=new MaxHeap<int>(); cout << "== 依次添加: ";
for(i=; i<len; i++)
{
cout << a[i] <<" ";
tree->insert(a[i]);
} cout << "\n== 最 大 堆: ";
tree->print(); i=;
tree->insert(i);
cout << "\n== 添加元素: " << i;
cout << "\n== 最 大 堆: ";
tree->print(); i=;
tree->remove(i);
cout << "\n== 删除元素: " << i;
cout << "\n== 最 大 堆: ";
tree->print();
cout << endl; return ;
}
二叉堆(最小堆)的实现文件(MinHeap.cpp)
/**
* 二叉堆(最小堆)
*
* @author skywang
* @date 2014/03/07
*/ #include <iomanip>
#include <iostream>
using namespace std; template <class T>
class MinHeap{
private:
T *mHeap; // 数据
int mCapacity; // 总的容量
int mSize; // 实际容量 private:
// 最小堆的向下调整算法
void filterdown(int start, int end);
// 最小堆的向上调整算法(从start开始向上直到0,调整堆)
void filterup(int start);
public:
MinHeap();
MinHeap(int capacity);
~MinHeap(); // 返回data在二叉堆中的索引
int getIndex(T data);
// 删除最小堆中的data
int remove(T data);
// 将data插入到二叉堆中
int insert(T data);
// 打印二叉堆
void print();
}; /*
* 构造函数
*/
template <class T>
MinHeap<T>::MinHeap()
{
new (this)MinHeap();
} template <class T>
MinHeap<T>::MinHeap(int capacity)
{
mSize = ;
mCapacity = capacity;
mHeap = new T[mCapacity];
}
/*
* 析构函数
*/
template <class T>
MinHeap<T>::~MinHeap()
{
mSize = ;
mCapacity = ;
delete[] mHeap;
} /*
* 返回data在二叉堆中的索引
*
* 返回值:
* 存在 -- 返回data在数组中的索引
* 不存在 -- -1
*/
template <class T>
int MinHeap<T>::getIndex(T data)
{
for(int i=; i<mSize; i++)
if (data==mHeap[i])
return i; return -;
} /*
* 最小堆的向下调整算法
*
* 注:数组实现的堆中,第N个节点的左孩子的索引值是(2N+1),右孩子的索引是(2N+2)。
*
* 参数说明:
* start -- 被下调节点的起始位置(一般为0,表示从第1个开始)
* end -- 截至范围(一般为数组中最后一个元素的索引)
*/
template <class T>
void MinHeap<T>::filterdown(int start, int end)
{
int c = start; // 当前(current)节点的位置
int l = *c + ; // 左(left)孩子的位置
T tmp = mHeap[c]; // 当前(current)节点的大小 while(l <= end)
{
// "l"是左孩子,"l+1"是右孩子
if(l < end && mHeap[l] > mHeap[l+])
l++; // 左右两孩子中选择较小者,即mHeap[l+1]
if(tmp <= mHeap[l])
break; //调整结束
else
{
mHeap[c] = mHeap[l];
c = l;
l = *l + ;
}
}
mHeap[c] = tmp;
} /*
* 删除最小堆中的data
*
* 返回值:
* 0,成功
* -1,失败
*/
template <class T>
int MinHeap<T>::remove(T data)
{
int index;
// 如果"堆"已空,则返回-1
if(mSize == )
return -; // 获取data在数组中的索引
index = getIndex(data);
if (index==-)
return -; mHeap[index] = mHeap[--mSize]; // 用最后元素填补
filterdown(index, mSize-); // 从index号位置开始自上向下调整为最小堆 return ;
} /*
* 最小堆的向上调整算法(从start开始向上直到0,调整堆)
*
* 注:数组实现的堆中,第N个节点的左孩子的索引值是(2N+1),右孩子的索引是(2N+2)。
*
* 参数说明:
* start -- 被上调节点的起始位置(一般为数组中最后一个元素的索引)
*/
template <class T>
void MinHeap<T>::filterup(int start)
{
int c = start; // 当前节点(current)的位置
int p = (c-)/; // 父(parent)结点的位置
T tmp = mHeap[c]; // 当前节点(current)的大小 while(c > )
{
if(mHeap[p] <= tmp)
break;
else
{
mHeap[c] = mHeap[p];
c = p;
p = (p-)/;
}
}
mHeap[c] = tmp;
} /*
* 将data插入到二叉堆中
*
* 返回值:
* 0,表示成功
* -1,表示失败
*/
template <class T>
int MinHeap<T>::insert(T data)
{
// 如果"堆"已满,则返回
if(mSize == mCapacity)
return -; mHeap[mSize] = data; // 将"数组"插在表尾
filterup(mSize); // 向上调整堆
mSize++; // 堆的实际容量+1 return ;
} /*
* 打印二叉堆
*
* 返回值:
* 0,表示成功
* -1,表示失败
*/
template <class T>
void MinHeap<T>::print()
{
for (int i=; i<mSize; i++)
cout << mHeap[i] << " ";
} int main()
{
int a[] = {, , , , , , , , };
int i, len=(sizeof(a)) / (sizeof(a[])) ;
MinHeap<int>* tree=new MinHeap<int>(); cout << "== 依次添加: ";
for(i=; i<len; i++)
{
cout << a[i] <<" ";
tree->insert(a[i]);
} cout << "\n== 最 小 堆: ";
tree->print(); i=;
tree->insert(i);
cout << "\n== 添加元素: " << i;
cout << "\n== 最 小 堆: ";
tree->print(); i=;
tree->remove(i);
cout << "\n== 删除元素: " << i;
cout << "\n== 最 小 堆: ";
tree->print();
cout << endl; return ;
}
二叉堆的C++测试程序
测试程序已经包含在相应的实现文件(MaxHeap.cpp)中了,下面只列出程序运行结果。
最大堆(MaxHeap.cpp)的运行结果:
== 依次添加:
== 最 大 堆:
== 添加元素:
== 最 大 堆:
== 删除元素:
== 最 大 堆:
最小堆(MinHeap.cpp)的运行结果:
== 依次添加:
== 最 小 堆:
== 添加元素:
== 最 小 堆:
== 删除元素:
== 最 小 堆:
PS. 二叉堆是"堆排序"的理论基石。以后讲解算法时会讲解到"堆排序",理解了"二叉堆"之后,"堆排序"就很简单了。
二叉堆(二)之 C++的实现的更多相关文章
- 笔试算法题(46):简介 - 二叉堆 & 二项树 & 二项堆 & 斐波那契堆
二叉堆(Binary Heap) 二叉堆是完全二叉树(或者近似完全二叉树):其满足堆的特性:父节点的值>=(<=)任何一个子节点的键值,并且每个左子树或者右子树都是一 个二叉堆(最小堆或者 ...
- 二叉堆(一)之 图文解析 和 C语言的实现
概要 本章介绍二叉堆,二叉堆就是通常我们所说的数据结构中"堆"中的一种.和以往一样,本文会先对二叉堆的理论知识进行简单介绍,然后给出C语言的实现.后续再分别给出C++和Java版本 ...
- 二叉堆(三)之 Java的实现
概要 前面分别通过C和C++实现了二叉堆,本章给出二叉堆的Java版本.还是那句话,它们的原理一样,择其一了解即可. 目录1. 二叉堆的介绍2. 二叉堆的图文解析3. 二叉堆的Java实现(完整源码) ...
- 在A*寻路中使用二叉堆
接上篇:A*寻路初探 GameDev.net 在A*寻路中使用二叉堆 作者:Patrick Lester(2003年4月11日更新) 译者:Panic 2005年3月28日 译者序 这一篇文章,是&q ...
- PHP利用二叉堆实现TopK-算法的方法详解
前言 在以往工作或者面试的时候常会碰到一个问题,如何实现海量TopN,就是在一个非常大的结果集里面快速找到最大的前10或前100个数,同时要保证 内存和速度的效率,我们可能第一个想法就是利用排序,然后 ...
- 【算法与数据结构】二叉堆和优先队列 Priority Queue
优先队列的特点 普通队列遵守先进先出(FIFO)的规则,而优先队列虽然也叫队列,规则有所不同: 最大优先队列:优先级最高的元素先出队 最小优先队列:优先级最低的元素先出队 优先队列可以用下面几种数据结 ...
- PHP-利用二叉堆实现TopK-算法
介绍 在以往工作或者面试的时候常会碰到一个问题,如何实现海量TopN,就是在一个非常大的结果集里面快速找到最大的前10或前100个数,同时要保证内存和速度的效率,我们可能第一个想法就是利用排序,然后截 ...
- Python实现二叉堆
Python实现二叉堆 二叉堆是一种特殊的堆,二叉堆是完全二元树(二叉树)或者是近似完全二元树(二叉树).二叉堆有两种:最大堆和最小堆.最大堆:父结点的键值总是大于或等于任何一个子节点的键值:最小堆: ...
- AC日记——二叉堆练习3 codevs 3110
3110 二叉堆练习3 时间限制: 3 s 空间限制: 128000 KB 题目等级 : 黄金 Gold 题解 题目描述 Description 给定N(N≤500,000)和N个整 ...
随机推荐
- Java 线程 — synchronized、volatile、锁
线程同步基础 synchronized 和volatile是Java线程同步的基础. synchronized 将临界区的内容上锁,同一时刻只有一个进程能访问该临界区代码 使用的是内置锁,锁一个时刻只 ...
- discuz x3在DIY模块中调用伪静态不成功,显示动态链接的解决办法
discuz x3在DIY模块中调用伪静态不成功,显示动态链接,然而其他的链接正常显示伪静态. 后台启用伪静态后,发现论坛版块.帖子点击链接,伪静态正常显示,然后在门户首页DIY显示的帖子,点进去后发 ...
- textViewDidChange: crashes in iOS 7
What's happening is that you're typing what is referred to as multistage text input, i.e. the input ...
- 使用Facebook的SDK判斷來訪者是否已經按讃并成為本站粉絲團的成員
今天公司裡要做活動,其中有一項活動內容是要求來訪者按一下facebook粉絲團的讃,按了讃之後贈送現金.Facebook被墻大家眾所周知,在百度搜了一下發現因為被墻的原因導致國內涉及到Facebook ...
- Javacript和AngularJS中的Promises
promise是Javascript异步编程很好的解决方案.对于一个异步方法,执行一个回调函数. 比如页面调用google地图的api时就使用到了promise. function success(p ...
- 了解 JavaScript (4)– 第一个 Web 应用程序
在下面的例子中,我们将要构建一个 Bingo 卡片游戏,每个示例演示 JavaScript 的不同方面,通过每次的改进将会得到最终有效的 Bingo 卡片. Bingo 卡片的内容 美国 Bingo ...
- mac 命令行 安装 需要管理员 权限
Please try running this command again as root/Administrator. sudo chown -R $USER /usr/local
- 如何通过Socket TCP发送并接收一个文件?
一.小结 1.大包发小包收,只发一次. 2.发时把文件扩展名,文件长度也随同一起发送,方便接收端接收时另存为正确的文件类型,并判断是否已经接收完毕. 如果不一起发送,分为文件扩展名,文件长度,文件内容 ...
- Android 解压boot.img
其实解压.打包boot.img没什么难度一看就会咯!! 1.先下附件:工具. 点击打开链接 6.0 KB, 下载次数: 60) 解压到bin文件夹里,方便以后使用. 2.解压boot ...
- Android开发:第四日番外——Assets文件夹和RAW文件夹区别
话说上回说到SQLite数据库,其中涉及到把已经设计好的数据库打包到APK中,提到可以放置在Assert文件夹或者RAW文件夹中,那么两者到底有什么区别呢?让我们来探究一下. 一.res/raw和as ...
