[NOI2010]能量采集 BZOJ2005 数学（反演）&&欧拉函数，分块除法

题目描述

栋栋有一块长方形的地，他在地上种了一种能量植物，这种植物可以采集太阳光的能量。在这些植物采集能量后，栋栋再使用一个能量汇集机器把这些植物采集到的能量汇集到一起。

栋栋的植物种得非常整齐，一共有n列，每列有m棵，植物的横竖间距都一样，因此对于每一棵植物，栋栋可以用一个坐标(x, y)来表示，其中x的范围是1至n，表示是在第x列，y的范围是1至m，表示是在第x列的第y棵。

由于能量汇集机器较大，不便移动，栋栋将它放在了一个角上，坐标正好是(0, 0)。

能量汇集机器在汇集的过程中有一定的能量损失。如果一棵植物与能量汇集机器连接而成的线段上有k棵植物，则能 量的损失为2k + 1。例如，当能量汇集机器收集坐标为(2, 4)的植物时，由于连接线段上存在一棵植物(1, 2)，会产生3的能量损失。注意，如果一棵植物与能量汇集机器连接的线段上没有植物，则能量损失为1。现在要计算总的能量损失。

下面给出了一个能量采集的例子，其中n = 5，m = 4，一共有20棵植物，在每棵植物上标明了能量汇集机器收集它的能量时产生的能量损失。

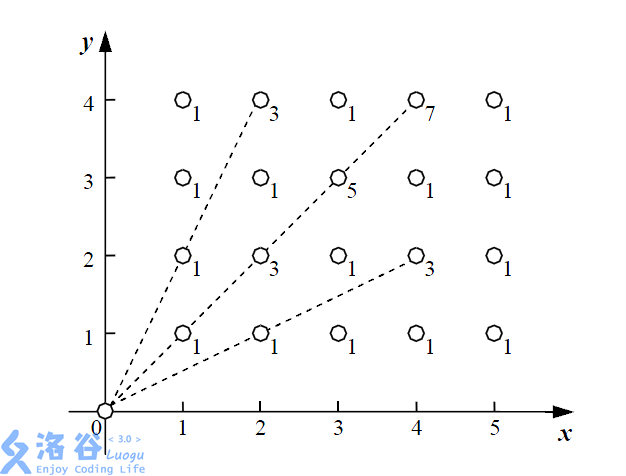
在这个例子中，总共产生了36的能量损失。

输入输出格式

输入格式：

仅包含一行，为两个整数n和m。

输出格式：

仅包含一个整数，表示总共产生的能量损失。

输入输出样例

输入样例#1：
复制

5 4

输出样例#1： 复制

36

输入样例#2： 复制

3 4

输出样例#2： 复制

20

说明

对于10%的数据：1 ≤ n, m ≤ 10；
对于50%的数据：1 ≤ n, m ≤ 100；
对于80%的数据：1 ≤ n, m ≤ 1000；
对于90%的数据：1 ≤ n, m ≤ 10,000；
对于100%的数据：1 ≤ n, m ≤ 100,000。

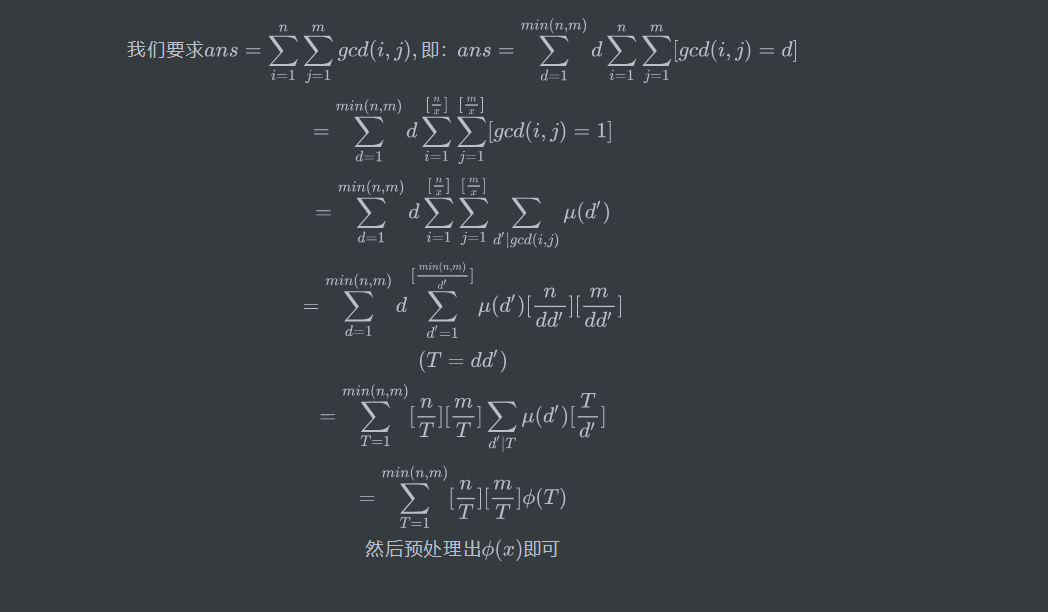
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstdlib>
#include<cstring>
#include<string>
#include<cmath>
#include<map>
#include<set>
#include<vector>
#include<queue>
#include<bitset>
#include<ctime>
#include<time.h>
#include<deque>
#include<stack>
#include<functional>
#include<sstream>
//#include<cctype>
//#pragma GCC optimize(2)
using namespace std;
#define maxn 200005
#define inf 0x7fffffff
//#define INF 1e18
#define rdint(x) scanf("%d",&x)
#define rdllt(x) scanf("%lld",&x)
#define rdult(x) scanf("%lu",&x)
#define rdlf(x) scanf("%lf",&x)
#define rdstr(x) scanf("%s",x)
#define mclr(x,a) memset((x),a,sizeof(x))
typedef long long  ll;
typedef unsigned long long ull;
typedef unsigned int U;
#define ms(x) memset((x),0,sizeof(x))
const long long int mod = 1e9 + 7;
#define Mod 1000000000
#define sq(x) (x)*(x)
#define eps 1e-5
typedef pair<int, int> pii;
#define pi acos(-1.0)
//const int N = 1005;
#define REP(i,n) for(int i=0;i<(n);i++)
typedef pair<int, int> pii;

inline int rd() {
	int x = 0;
	char c = getchar();
	bool f = false;
	while (!isdigit(c)) {
		if (c == '-') f = true;
		c = getchar();
	}
	while (isdigit(c)) {
		x = (x << 1) + (x << 3) + (c ^ 48);
		c = getchar();
	}
	return f ? -x : x;
}

ll gcd(ll a, ll b) {
	return b == 0 ? a : gcd(b, a%b);
}
int sqr(int x) { return x * x; }

/*ll ans;
ll exgcd(ll a, ll b, ll &x, ll &y) {
	if (!b) {
		x = 1; y = 0; return a;
	}
	ans = exgcd(b, a%b, x, y);
	ll t = x; x = y; y = t - a / b * y;
	return ans;
}
*/

int tot;
int vis[maxn];
ll phi[maxn], sum[maxn], p[maxn], n, m;
void init() {
	phi[1] = 1;
	for (int i = 2; i <= maxn; i++) {
		if (!vis[i]) {
			p[++tot] = i; phi[i] = i - 1;
		}
		for (int j = 1; j <= tot && i*p[j] <= maxn; j++) {
			vis[i*p[j]] = 1;
			phi[i*p[j]] = phi[i] * phi[p[j]];
			if (i%p[j] == 0) {
				phi[i*p[j]] = phi[i] * p[j]; break;
			}
		}
	}
}

int main()
{
//	ios::sync_with_stdio(0);
	rdllt(n); rdllt(m);
	init(); ll ans = 0;
//	cout << phi[10] << ' ' << phi[5] << endl;
	for (int i = 1; i <= maxn; i++)sum[i] = sum[i - 1] + phi[i];
	for (int l = 1, r; l <= min(n, m); l = r + 1) {
		r = min(n / (n / l), m / (m / l));
		ans += 1ll * (sum[r] - sum[l - 1])*(n / l)*(m / l);
	}
	cout << (ll)(2ll * ans - n * m) << endl;
	return 0;
}