《Algorithms 4th Edition》读书笔记——2.4 优先队列(priority queue)-Ⅵ

· 学后心得体会与部分习题实现

心得体会：

曾经只是了解了优先队列的基本性质，并会调用C++ STL库中的priority_queue以及 java.util.PriorityQueue<E>中的优先队列封装类，但是没有看过源码，也并不曾知道实现方法用到了堆结构。

优先队列通过堆进行插入元素和删除最小元素的两种高效操作来维护元素集合，每个操作的时间都为对数级（logN）。堆结构及其操作符合优先队列的全部特点，另附有高效率，用来描述与实现优先队列再合适不过。

在学习过程中，在对于堆结构众多操作的巧妙操作中，令我印象深刻的是两种操作：swim() 和 sink()操作，即对于新元素或者删除最大（或最小）根节点后的新根的上浮和下沉操作（有些教材上称为上滤和下滤操作。其命名个人YY的含义是：由于swim() 和sink() 操作是用在insert() 和 delMax() 两个方法中的子方法，用于过滤二叉堆，使其重构成完全二叉树结构。）。

该方法的效率证明可以参看《Introduction to Algorithm》（《算法导论》）中的 6.2 维护堆的性质：

通过对优先队列的学习，自己用Java实现了一下。并可以用以下这个个人编写的二叉堆的实现，完成《Algorithms 4th Edition》中的2.4.1和2.4.6。

 import java.math.*;

 public class MaxPQ<Key extends Comparable<Key>> {
     private Key[] pq;
     private int N = 0;

     @SuppressWarnings("unchecked")
     public MaxPQ(int maxN) {
         pq = (Key[]) new Comparable[maxN + 1];
     }

     public boolean isEmpty() {
         return N == 0;
     }

     public int size() {
         return N;
     }

     public void insert(Key v) {
         pq[++N] = v; swim(N);
     }

     private void exch(int i, int j) {
         Key t = pq[i]; pq[i] = pq[j]; pq[j] = t;
     }

     public Key delMax() {
         Key max = pq[1];
         exch(1, N--);
         pq[N + 1] = null;
         sink(1);
         return max;
     }

     private boolean less(int i, int j) {
         return pq[i].compareTo(pq[j]) < 0;
     }

     private void swim(int k) {
         while(k > 1 && less(k / 2, k)) {
             exch(k / 2, k);
             k  =k / 2;
         }
     }

     private void sink(int k) {
         while(2 * k <= N) {
             int j  = 2 * k;
             if(j < N && less(j, j + 1)) j++;
             if(!less(k, j)) break;
             exch(k , j);
             k = j;
         }
     }

     public void prtPQ() {
         for(int i = 1; i <= N; i++) {
             System.out.print(pq[i] + " ");
         }
         System.out.println();
     }
 }

以下是对应部分题目实现（只给出Main部分）：

 import java.math.*;
 import java.util.*;

 public class Main {
     public static void main(String[] args) {
         MaxPQ<Character> PQ = new MaxPQ<Character>(1000);
         String op = "PRIO*R**I*T*Y***QUE***U*E";
         int cnt = 0;
         for(int i = 0; i < op.length(); i++) {
             if(op.charAt(i) == '*') {
                 System.out.println(++cnt + ". Max is " + PQ.delMax());
             } else {
                 PQ.insert(op.charAt(i));
             }
         }

     }
 }

2.4.1

运行结果：

 import java.math.*;
 import java.util.*;

 public class Main {
     public static void main(String[] args) {
         MaxPQ<Character> PQ = new MaxPQ<Character>(1000);
         String op = "PRIO*R**I*T*Y***QUE***U*E";
         int cnt = 0;
         for(int i = 0; i < op.length(); i++) {
             if(op.charAt(i) == '*') {
                 PQ.delMax();
             } else {
                 PQ.insert(op.charAt(i));
             }
             System.out.print(++cnt + ". ");
             PQ.prtPQ();
         }
     }
 }

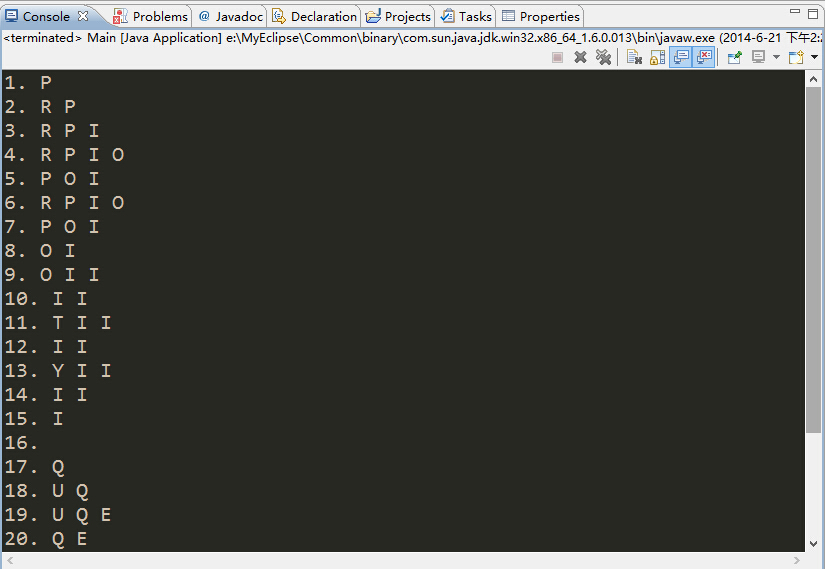
2.4.6

 

运行结果：

---

至此，对于优先队列的学习告一段落。笔者一直相信唯 有坚持者才能把算法学的精通，所以算法的学习之路好会坚持下去。一直用luc的文章 http://zh.lucida.me/blog/on- learning-algorithms/ 来激励自己，相信自己终有一天，能达到自己理想的高度。如此才不后悔。

---