CTF_RSA解密学习

00X00 、先看了一边李永乐老师的视频

https://www.bilibili.com/video/av26639065/

00X01、对称、非对称算法了解

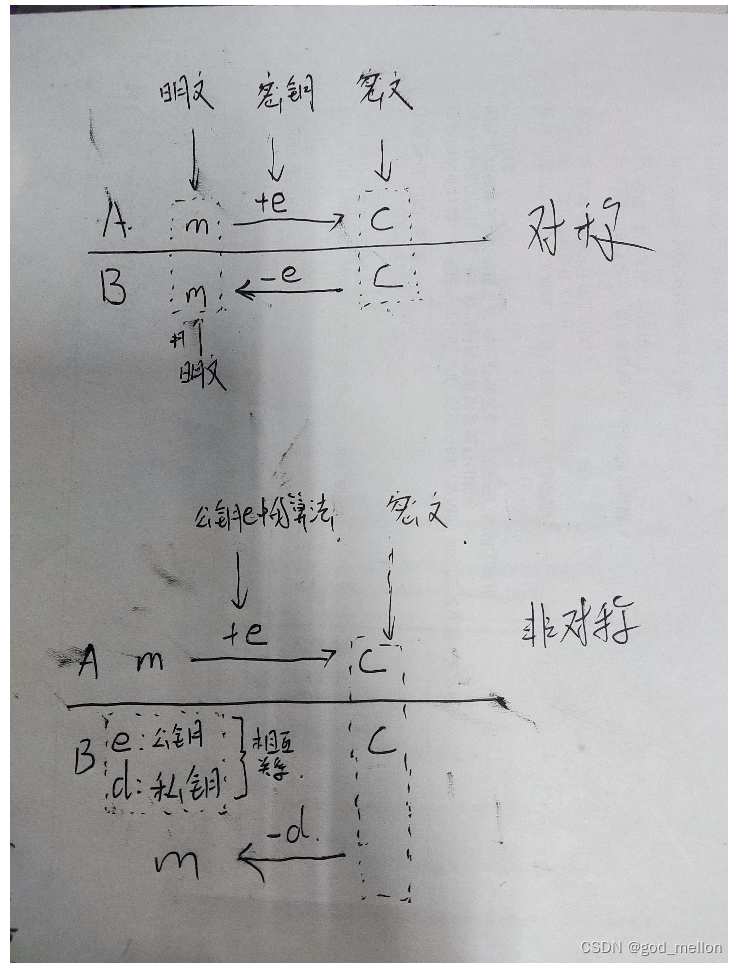
对称算法，加解密双方使用一个密钥。即加密秘钥和解密秘钥相同。
对称加密又分为：分组加密和流加密

常见的分组算法有：DES、3DES、DESX、Blowfish、IDEA、RC2、

RC5、RC6和AES，以及中国的SSF33、SM1、SM4。

分组加密又可以根据其迭代模式分为ECB，CBC，OFB，CFB，CTR。

非对称算法也叫公钥算法，在公钥密码系统中，加密和解密使用的是不同的密钥，这两个密钥之间存在着相互依存关系：即用其中任一个密钥加密的信息只能用另一个密钥进行解密。
这使得通信双方无需事先交换密钥就可进行保密通信。其中加密密钥和算法是对外公开的，人人都可以通过这个密钥加密文件然后发给收信者，这个加密密钥又称为公钥；
而收信者收到加密文件后,它可以使用他的解密密钥解密，这个密钥是由他自己私人掌管的，并不需要分发，因此又成称为私钥，这就解决了密钥分发的问题。

主要的公钥算法有： RSA、 DSA、 DH 和 ECC。

00X02、RSA简介

RSA 加密算法是一种非对称加密算法。在公开密钥加密和电子商业中 RSA 被广泛使用。RSA 是 1977 年由罗纳德 · 李维斯特（Ron Rivest）、阿迪 · 萨莫尔（Adi Shamir）和伦纳德 · 阿德曼（Leonard Adleman）一起提出的。RSA 就是他们三人姓氏开头字母拼在一起组成的。

RSA 算法的可靠性由极大整数因数分解的难度决定。换言之，对一极大整数做因数分解愈困难，RSA 算法愈可靠。假如有人找到一种快速因数分解的算法的话，那么用 RSA 加密的信息的可靠性就肯定会极度下降。但找到这样的算法的可能性是非常小的。如今，只有短的 RSA 密钥才可能被强力方式解破。到 2017 年为止，还没有任何可靠的攻击 RSA 算法的方式。

00x03、RSA算法原理

1、公钥与私钥的产生：

(1)进行加密之前，首先找出2个不同的大质数p和q

(2)计算n=p*q

(3)根据欧拉函数，求得φ(n)=φ§φ(q)=(p−1)(q−1)

(4)找出一个公钥e，e要满足: 1<e<φ(n) 的整数，且使e和φ(N)互质。

(5)根据e*d除以φ(n)余数为1，找到私钥d。

(6)所以,公钥就是(n,e) 私钥就是(n,d)

2、消息加密:

m^e除以n求余数即为c(密文)

也就是说RSA加密是对明文的E次方后除以N后求余数的过程。
从通式可知，只要知道E和N任何人都可以进行RSA加密了，所以说E、N是RSA加密的密钥，也就是说E和N的组合就是公钥，我们用(E,N)来表示公钥

公钥＝(E,N)公钥＝(E,N)

3、消息解密:

c^d除以n求余数即为m(明文)

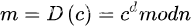
也就是说对密文进行D次方后除以N的余数就是明文，这就是RSA解密过程。知道D和N就能进行解密密文了，所以D和N的组合就是私钥。

 私钥＝(D,N)私钥＝(D,N)

4、如下

公钥	（E，N）
私钥	（D,N）
密钥对	（E，D，N）
加密	密文＝明文EmodN密文＝m^EmodN
解密	明文＝密文DmodN明文＝ c^DmodN

5、小结

求N	N＝ p ＊ q ；p，q为质数
求φ(n)	φ(n)=φ§φ(q)=(p−1)(q−1)
求E	找出一个公钥e，e要满足: 1<e<φ(n) 的整数，且使e和φ(N)互质。
求D	根据e*d除以φ(n)余数为1，找到私钥d。

00x04、实践

1、求n

我们准备两个很小对质数，
p ＝ 17
q ＝ 19
n ＝ p ＊ q ＝ 323

2、求φ(n)

φ(n)=φ§φ(q)=(17−1)(19−1)=144

3、求e

求E必须要满足2个条件：1 < e < L ，gcd（e，φ(n)）=1
即1 < e < 144，gcd（e，144）＝ 1
e和144互为质数，5显然满足上述2个条件
故E ＝ 5

4、求d

求D也必须满足2个条件：1 < d < φ(n)，e＊d mod φ(n)＝ 1
即1 < e < 144，5 ＊ d mod 144 ＝ 1
显然当d＝ 29 时满足上述两个条件
1 < 29 < 144
5＊29 mod 144 ＝ 145 mod 144 ＝ 1
此时私钥＝（d，n）＝（29，323）

5、加密

准备的明文必须时小于N的数，因为加密或者解密都要mod N其结果必须小于N
假设明文＝ 123
则密文＝明文EmodN
则密文＝明文EmodN＝1235mod323=225密文＝明文EmodN＝1235mod323=225

q = 19

p = 17

e = 5

n = q * p

d = 29

m1=123

c1= pow(m1, e, n)

print(c1)

6、解密

明文＝密文DmodN＝225^29mod323=123
解密后的明文为123。



# 解密

q = 19

p = 17

e = 5

n = q * p

d = 29

m1=123

c1= pow(m1, e, n)

print(c1)

c=225

#m=10# print(n)

m2= pow(c, d, n)

print(m2)

225

123