数据结构与算法--递归(recursion)

递归的概念

简单的说: 递归就是方法自己调用自己,每次调用时传入不同的变量.递归有助于编程者解决复杂的问题,同时可以让代码变得简洁。

递归调用机制

我列举两个小案例,来帮助大家理解递归

1、打印问题

2、阶乘问题

//输出什么?
public static void test(int n) {
if (n > 2) {
    test(n - 1);
}
System.out.println("n=" + n);
}

//阶乘
public static int factorial(int n) {
if (n == 1) {
return 1;
} else {
return factorial(n - 1) * n;
}}

3、使用图解说明递归的调用机制

递归能解决什么样的问题

1、各种数学问题如: 8皇后问题 , 汉诺塔, 阶乘问题, 迷宫问题, 球和篮子的问题(google编程大赛)

2、各种算法中也会使用到递归，比如快排，归并排序，二分查找，分治算法等.

3、将用栈解决的问题-->第归代码比较简洁

递归需要遵守的重要规则

1)执行一个方法时，就创建一个新的受保护的独立空间(栈空间)

2)方法的局部变量是独立的，不会相互影响, 比如n变量

3)如果方法中使用的是引用类型变量(比如数组)，就会共享该引用类型的数据.

4)递归必须向退出递归的条件逼近，否则就是无限递归,出现StackOverflowError，死龟了:)

5)当一个方法执行完毕，或者遇到return，就会返回，遵守谁调用，就将结果返回给谁，同时当方法执行完毕或者返回时，该方法也就执行完毕。

递归应用场景

迷宫问题(回溯)， 递归(Recursion)

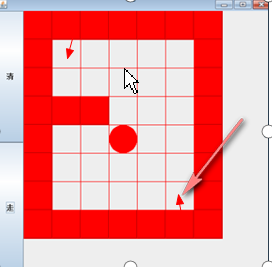
迷宫问题：将左上角小球一步一步走到右下角位置。怎么走？

分析：

1、我们可以用一个二维数组map[8][7]表示地图，i,j 表示从地图的哪个位置开始出发 (1,1)

2、如果小球能到 map[6][5] 位置，则说明通路找到.

3、约定： 当map[i][j] 为 0 表示该点没有走过 当为 1 表示墙 ； 2 表示通路可以走 ； 3 表示该点已经走过，但是走不通

4、在走迷宫时，需要确定一个策略(方法) 下->右->上->左 , 如果该点走不通，再回溯

实现代码:

/**
     *
     * @param map 表示地图
     * @param i 从哪个位置开始找
     * @param j
     * @return 如果找到通路，就返回true, 否则返回false
     */
    public static boolean setWay(int[][] map, int i, int j) {
        if(map[6][5] == 2) { // 通路已经找到ok
            return true;
        } else {
            if(map[i][j] == 0) { //如果当前这个点还没有走过
                //按照策略 下->右->上->左  走
                map[i][j] = 2; // 假定该点是可以走通.
                if(setWay(map, i+1, j)) {//向下走
                    return true;
                } else if (setWay(map, i, j+1)) { //向右走
                    return true;
                } else if (setWay(map, i-1, j)) { //向上
                    return true;
                } else if (setWay(map, i, j-1)){ // 向左走
                    return true;
                } else {
                    //说明该点是走不通，是死路
                    map[i][j] = 3;
                    return false;
                }
            } else { // 如果map[i][j] != 0 , 可能是 1， 2， 3
                return false;
            }
        }
    }

public static void main(String[] args) {
        // 先创建一个二维数组，模拟迷宫
        // 地图
        int[][] map = new int[8][7];
        // 使用1 表示墙
        // 上下全部置为1
        for (int i = 0; i < 7; i++) {
            map[0][i] = 1;
            map[7][i] = 1;
        }

        // 左右全部置为1
        for (int i = 0; i < 8; i++) {
            map[i][0] = 1;
            map[i][6] = 1;
        }
        //设置挡板, 1 表示
        map[3][1] = 1;
        map[3][2] = 1;
//        map[1][2] = 1;
//        map[2][2] = 1;

        // 输出地图
        System.out.println("地图的情况");
        for (int i = 0; i < 8; i++) {
            for (int j = 0; j < 7; j++) {
                System.out.print(map[i][j] + " ");
            }
            System.out.println();
        }

        //使用递归回溯给小球找路
        setWay(map, 1, 1);
        //setWay2(map, 1, 1);

        //输出新的地图, 小球走过，并标识过的递归
        System.out.println("小球走过，并标识过的 地图的情况");
        for (int i = 0; i < 8; i++) {
            for (int j = 0; j < 7; j++) {
                System.out.print(map[i][j] + " ");
            }
            System.out.println();
        }

    }

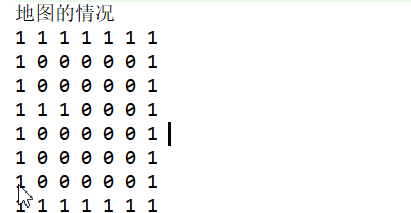
输出

地图的情况
1 1 1 1 1 1 1
1 0 0 0 0 0 1
1 0 0 0 0 0 1
1 1 1 0 0 0 1
1 0 0 0 0 0 1
1 0 0 0 0 0 1
1 0 0 0 0 0 1
1 1 1 1 1 1 1
小球走过，并标识过的 地图的情况
1 1 1 1 1 1 1
1 2 0 0 0 0 1
1 2 2 2 0 0 1
1 1 1 2 0 0 1
1 0 0 2 0 0 1
1 0 0 2 0 0 1
1 0 0 2 2 2 1
1 1 1 1 1 1 1 

上面代码示例 不走策略是   下->右->上->左   ，那么我们也可以改变策略，改成 上->右->下->左 ，那又怎么写，会怎么走呢。

就是改变上面代码 if else 顺序即可。

这就是简单运用 递归 回溯算法的应用。