[NOIP10.5模拟赛]3.c题解--思维

题目链接

这次不咕了

https://www.luogu.org/problemnew/show/AT2389

闲扯

考场20分爆搜走人 \cy

话说这几天T3都很考验思维啊

分析

我们先钦定一只鸡(虽然考试时是苹果但是我觉得杀鸡更亲切(因为我们某位同学))先必须活着,所以呢我们需要逆着倒推每一组关系,然后把为了保证我们钦定的鸡活着必须杀的鸡放进一个集合,为了方便表示用\(f[now][i]=1/0\)表示钦定第now只鸡活着第\(i\)只鸡最终有没有加入集合;

对于一对关系\((a,b)\),如果\(f[now][a]=1\),那么\(f[now][b]\)显然必须置为1加入集合,因为a这只鸡为了保证now不被杀掉已经在一条边中被杀掉,为了保证当前这条边合法则必须杀掉b(注意关系是倒着枚举的)

但这是有个问题,就是如果\(f[now][a]\)&\(f[now][b]=1\)说明关系矛盾,\(now\)必须死,为啥?

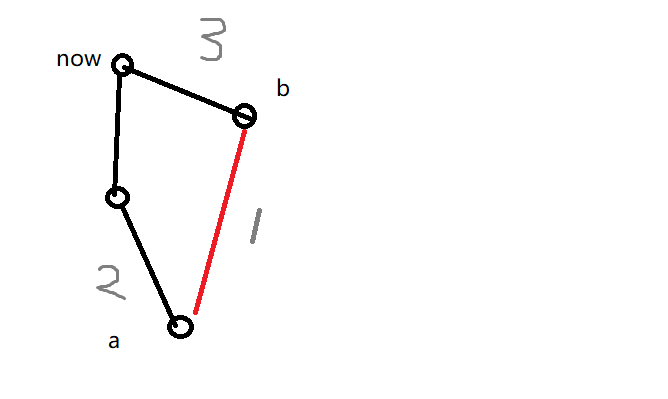
我们考虑没有这种情况,将鸡视为点,关系视为边,显然我们的集合实际上是一个以now为根节点的树,而且满足\(x\)到\(fa[x]\)的关系比\(fa[x]\)到\(fa[fa[x]]\)的边次序要早(但是在枚举时因为是倒着枚举是先构成前者)

如果这时候加入一条边连接两个已经在集合中的点\((a,b)\),由于1号边次序要比2,3边早,所以先必须在a,b中选一个杀死满足1号边的关系.但是我们为了让now不死,我们必须要让a点因为2号边死去,b因为3号边死去.出现了这种情况显然就不可能了,所以需要记录一下\(now\)存活是不可行的

最后假设已经遍历完,获得钦定每个点活着的时候要杀掉的鸡的集合(虽然不一定合法)

然后对于每一只鸡判断是否能与编号靠后的另一只鸡一起存活,怎么判断呢?

首先如果如果其中有只鸡本身无法存活则特判continue,但是还有种非法的情况,就是存在一只鸡为了满足\(a\)活必须死,又同时满足\(b\)活下来也必须死.这样的话\(a,b\)无法同时存活

这其实很显然的,边有先后顺序,你为了满足其中一只鸡另一只鸡就一定不可行,所以这种情况我们可以把两个鸡的集合并起来看看有没有1存在

代码

#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#include <cctype>
#include <iostream>
#include <bitset>
#define ll long long
#define ri register int
using std::min;
using std::bitset;
using std::max;
template <class T>inline void read(T &x){
    x=0;int ne=0;char c;
    while(!isdigit(c=getchar()))ne=c=='-';
    x=c-48;
    while(isdigit(c=getchar()))x=(x<<3)+(x<<1)+c-48;
    x=ne?-x:x;return ;
}
const int maxn=405;
const int inf=0x7fffffff;
bitset <maxn> o[maxn];
bool ok[maxn];
int a[100005],b[100005],m,n;
int main(){
    int x,y;
    bool flag=0;
    read(n),read(m);
    for(ri i=1;i<=m;i++)read(a[i]),read(b[i]);
    for(ri i=1;i<=n;i++){
        o[i][i]=1;flag=0;
        for(ri j=m;j>=1&&!flag;j--){
            x=o[i][a[j]],y=o[i][b[j]];
            if(x&y){
                ok[i]=1;
                flag=1;continue;
            }
            if(x){o[i][b[j]]=1;}
            if(y){o[i][a[j]]=1;}
        }
    }
    ll ans=0;
    for(ri i=1;i<=n;i++){
        if(ok[i])continue;
        for(ri j=i+1;j<=n;j++){
            if(ok[j])continue;
            if(!((o[i]&o[j]).any()))ans++;
        }
    }
    printf("%lld\n",ans);
    return 0;
}