------------恢复内容开始------------

据新闻报道数学天才陶哲轩和3个物理学家研究出一个只用特征值就可以计算矩阵特征向量的公式, 我感觉很有趣, 这应该能够应用在很多领域中, 所以仔细研究了一波。研究公式耗费了我大半天, 我把所有的equation都推导了一遍, 也给出了一些我的看法, 现在把它们总结出来, 方便后人参考. 我给出了Cauchy-Binet公式(原文引理1)的更广义形式及其怎么过程, 对该公式取特殊条件即可证明引理2.(该引理就是全文的主要结论). 不过相比之下, 还是陶哲轩对于引理2得证明更简洁, 虽然没有用到引理1。

我的证明有些地方可能不严谨, 欢迎读者批评指正。

----司徒鲜生- 2019年@上海天文台

  • 参考(文献)

    新闻报道(微信): 3个搞物理的颠覆了数学常识, 数学天才陶哲轩: 我开始压根不相信

  • 参考(文献)

1.说明

2.化简的方法

 3.  特征分解的方法

4.  联立可得

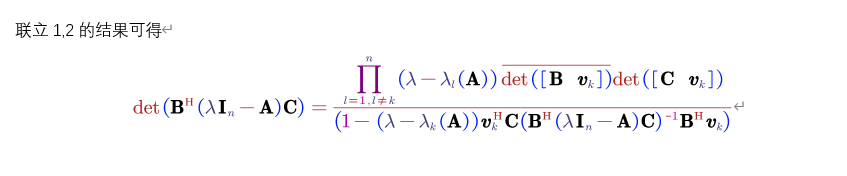
5.  特殊情况1

6.  特殊情况2

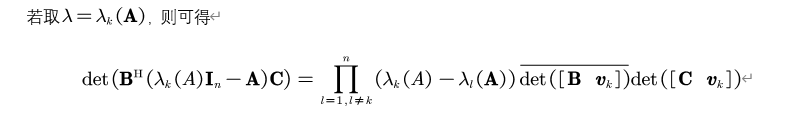
7.  特殊情况3

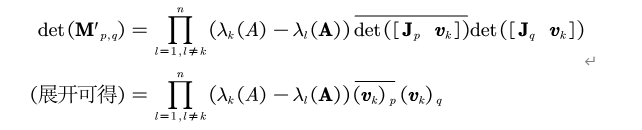8.  特殊情况4

9.  解释及备注

10. 特征向量归一化的验证

Cauchy-Binet公式的证明 及 对Denton et al. (2019)的个人注(1)的更多相关文章

  1. 一个形式较精细的Strling公式的证明

    近日整理书稿,在整理至Strling公式处时,发现当时数学老师所讲的是形式比较精细的一种: Strling公式:\(n!=\sqrt{2\pi n}\left(\dfrac{n}{\mathrm{e} ...

  2. 关于后缀间$LCP$的一些公式的证明

    目录 关于\(LCP\)有如下两个公式: \(LCP~Lemma\) 的证明: \(LCP~Theorem\) 的证明: 关于\(LCP\)有如下两个公式: \(LCP~Lemma:\) 对任意 \( ...

  3. RSA算法原理——（3）RSA加解密过程及公式论证

    上期(RSA简介及基础数论知识)为大家介绍了:互质.欧拉函数.欧拉定理.模反元素 这四个数论的知识点,而这四个知识点是理解RSA加密算法的基石,忘了的同学可以快速的回顾一遍. 一.目前常见加密算法简介 ...

  4. 狄利克雷卷积&莫比乌斯反演证明

    狄利克雷卷积简介 卷积这名字听起来挺学究的,今天学了之后发现其实挺朴实hhh. 卷积: "(n)"表示到n的一个范围. 设\(f,g\)是两个数论函数(也就是说,以自然数集为定义域 ...

  5. 用积分方法求K次方和数列公式

    这是我很早以前在高中时发现的一个通用计算K次方和数列公式的方法,很特别的地方是用了微积分中的积分方法.目前我还没有发现有谁提出和我一样的方法,如果哪位读者有相关发现,麻烦告知我. 大家很多人都知道高斯 ...

  6. 数学算法（一）：快速求斐波那契数第n项通过黄金分割率公式

    有一个固定的数学公式= =,不知道的话显然没法应用 首先黄金分割率接近于这个公式, (以下为黄金分割率与斐波那契的关系,可跳过) 通过斐波那契数列公式 两边同时除以 得: (1) 注意后一项比前一项接 ...

  7. 【转】【关于 A^x = A^(x % Phi(C) + Phi(C)) (mod C) 的若干证明】【指数循环节】

    [关于 A^x = A^(x % Phi(C) + Phi(C)) (mod C) 的若干证明][指数循环节] 原文地址:http://hi.baidu.com/aekdycoin/item/e493 ...

  8. 数学-Matrix Tree定理证明

    老久没更了,冬令营也延期了(延期后岂不是志愿者得上学了?) 最近把之前欠了好久的债,诸如FFT和Matrix-Tree等的搞清楚了(啊我承认之前只会用,没有理解证明--),FFT老多人写,而Matri ...

  9. office2007/2010/2013输入公式的正确方式

    博客中的文章均为 meelo 原创,请务必以链接形式注明本文地址 理工科的学生,写报告.写论文那面需要输入公式,过去大家常用的公式编辑器是mathtype,虽然功能强大,但输入极为不方便,输入个指数. ...

随机推荐

  1. idea破解版安装、配置jdk以及建立一个简单的maven工程

    idea破解版安装.配置jdk,配置jdk环境变量以及建立一个简单的maven工程 一.idea破解版以及配置文件下载 下载网址:https://pan.baidu.com/s/1yojA51X1RU ...

  2. sudo 提示 'xxx is not in the sudoers file.This incident will be reported.的解决方法'

    在使用 Linux 的过程中,有时候需要临时获取 root 权限来执行命令时,一般通过在命令前添加 sudo 来解决. 但是第一次使用 sudo 时,有可能会得到这样一个错误提示 xxx is not ...

  3. go 学习笔记之解读什么是defer延迟函数

    Go 语言中有个 defer 关键字,常用于实现延迟函数来保证关键代码的最终执行,常言道: "未雨绸缪方可有备无患". 延迟函数就是这么一种机制,无论程序是正常返回还是异常报错,只 ...

  4. 调用对象 “ha-datastoresystem”的“HostDatastoreSystem.QueryVmfsDatastoreCreateOptions” 失败。

    VMware vSphere Client上显示:在 ESXi“10.10.10.3”上调用对象 “ha-datastoresystem”的“HostDatastoreSystem.QueryVmfs ...

  5. 小白学 Python（2）：基础数据类型（上）

    人生苦短,我选Python 引言 前文传送门 小白学 Python(1):开篇 接触一门新的语言,肯定要先了解它的基础数据类型.啥?你问我为啥要先了解基础数据类型? 为了你的生命安全,还是乖乖听我 B ...

  6. 使用Xming显示Oracle Linux图形界面

    如果你在尝试各种官方说明文档中的方法之后,xclock仍然无法远程显示. 系统 Win10 - Oracle Linux 7.5 Xming的文档以及网上教程都说的是Xming相关的配置 但是,要显示 ...

  7. 《深入理解Java虚拟机》-----第13章 线程安全与锁优化

    概述 在软件业发展的初期,程序编写都是以算法为核心的,程序员会把数据和过程分别作为独立的部分来考虑,数据代表问题空间中的客体,程序代码则用于处理这些数据,这种思维方式直接站在计算机的角度去抽象问题和解 ...

  8. 实验吧之【简单的登录题(】CBC字节反转攻击)

    开始刷ctf题吧  慢慢来. 实验吧---简单的登录题 题目地址:http://ctf5.shiyanbar.com/web/jiandan/index.php 随便提交一个id,看到后台set了两个 ...

  9. js中submit和button的区别

    今天写一个js验证 遇到点小坑 记录一下 button-普通按钮,submit-提交按钮. submit是button的一个特例,也是button的一种,它把提交这个动作自动集成了,submit和bu ...

  10. Tensorflow从开始到放弃（技术篇）

    在gpu中运行 tf.device("/gpu:1") 有时候这个是会出问题的,即便你在有名称为1的gpu时.有的操作是不能支持gpu的,应该为session添加一些配置: pyt ...