Iterative learning control for linear discrete delay systems via discrete matrix delayed exponential function approach

对于一类具有随机变迭代长度的问题，如功能性电刺激，用户可以提前结束实验过程，论文也是将离散矩阵延迟指数函数引入到状态方程中。

论文中关于迭代长度有三个定义值：\(Z^Ta\) 为最小的实验长度，\(Z^Td\) 为期望实验长度，\(Z^Tk\) 为k次迭代的实验长度。

柯西状态方程如下：

\[\begin{aligned}
x(t+1) &=A x(t)+A_{1} x(t-\sigma)+f(t), \quad t \in \mathbb{Z}_{0}^{\infty} \\
x(t) &=\varphi(t), \quad t \in \mathbb{Z}_{-\sigma}^{0}
\end{aligned}
\]

引入离散矩阵延迟指数函数，状态x(k)的解为：

\[\begin{aligned}
x(t)=& A^{t} e_{\sigma}^{B_{1} t} A^{-\sigma} \varphi(-\sigma)+\sum_{j=-\sigma+1}^{0} A^{(t-j)} e_{\sigma}^{B_{1}(t-\sigma-j)}[\varphi(j)-A \varphi(j-1)] \\
&+\sum_{j=1}^{t} A^{(t-j)} e_{\sigma}^{B_{1}(t-\sigma-j)} f(j-1)
\end{aligned}
\]

随机变迭代实验长度内容部分：

存在两种情况：1. \(T_k>T_d\)，2. \(T_a<T_k<T_d\) 。对于第一种情况，只用Td以内的数据用来更新输入信号，对于第二情况只用\(Tk\)之内的数据进行更新。

η_k (t)为伯努利分布，其中值1表示以p(t)的概率运行到t时刻，值0表示以1-p(t)的概率不能运行到时刻t。对于Ta到Td这段时间的概率计算公式如下：

\[p(t)=\left\{\begin{array}{ll}
1, & t \in \mathbb{Z}_{0}^{T_{a}} \\
\sum_{i=t}^{T_{d}} p_{i}, & t \in \mathbb{Z}_{T_{a+1}}^{T_{d}} .
\end{array}\right.
\]

举一个例子通俗地讲一下，上面地内容主要是用在算法收敛性证明的。前6次迭代实验的长度如下图所示，1为上面伯努利分布的1事件，0同理。



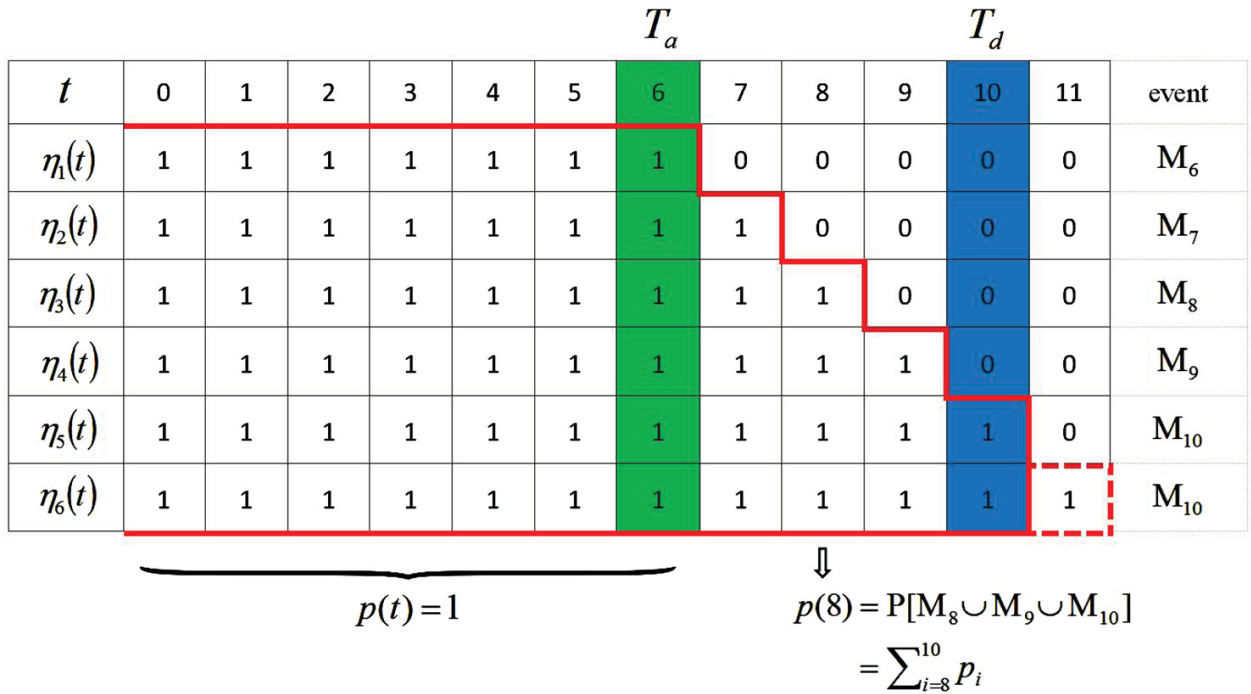
把Ta=6作为最小的运行时刻，期望运行时刻为Td=10，第一次迭代的终止时刻为6，把这个事件称之为M6，第六次迭代时，到T=11结束，即运行时刻大于Td，把这种情况同样视为M10。在上面的这张表中，运行到[7,10]的概率如下所示：其中pi为事件Mi发生的概率。那么系统能运行到时刻8的概率p(8)等于大于时刻8事件的概率3/5。

p(t)的概率表达式为：

\[p(t)=\mathbf{P}\left[\bigcup_{i=t}^{10} \mathbf{M}_{i}\right]=\sum_{i=t}^{10} \mathbf{P}\left[\mathbf{M}_{i}\right]=\sum_{i=t}^{10} p_{i}
\]

关于误差的定义

由于存在实际实验长度小于期望长度，所以这部分的误差当作0来计算：

\[\tilde{e}_{k}(t):=\eta_{k}(t) e_{k}(t)=\left\{\begin{array}{ll}
e_{k}(t), & t \in \mathbb{Z}_{0}^{T_{k}} \\
0, & t \in \mathbb{Z}_{T_{k+1}}^{T_{d}}
\end{array}\right.
\]

两种学习控制律

\[u_{k+1}(t)=u_{k}(t)+L_{1} \tilde{e}_{k}(t), \quad t \in \mathbb{Z}_{0}^{T_{d}}
\]

\[u_{k+1}(t)=u_{k}(t)+L_{2} \tilde{e}_{k}(t+1), \quad t \in \mathbb{Z}_{0}^{T_{d}}
\]

对于(9)式要把期望时间间隔设置为0到Td+1。算法的收敛性略（其实是我不会）。

代码见GITHUB