2019-2020 ACM-ICPC Brazil Subregional Programming Contest (11/13)
\(2019-2020\ ACM-ICPC\ Brazil\ Subregional\ Programming\ Contest\)
\(A.Artwork\)
并查集，把检测区域能在一起的检测器放在一个并查集里，然后判断是否有一个集合能够封住左边和上边的其中一个还有右边和下边的其中一个即可
//#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<bits/stdc++.h>
using namespace std;
function<void(void)> ____ = [](){ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);};
const int MAXN = 1111;
const int INF = 0x3f3f3f3f;
int n,m,k,root[MAXN],tot;
pair<pair<int,int>,int> sensor[MAXN];
vector<int> SET[MAXN];
map<int,int> mp;
int findx(int x){
if(x!=root[x]) root[x] = findx(root[x]);
return root[x];
}
int dist(const pair<int,int> &A, const pair<int,int> &B){
return (A.first-B.first)*(A.first-B.first)+(A.second-B.second)*(A.second-B.second);
}
int main(){
scanf("%d %d %d",&n,&m,&k);
for(int i = 1; i <= k; i++) scanf("%d %d %d",&sensor[i].first.first,&sensor[i].first.second,&sensor[i].second);
for(int i = 1; i <= k; i++) root[i] = i;
for(int i = 1; i <= k; i++) for(int j = i+1; j <= k; j++){
int fa = findx(i);
int fb = findx(j);
if(fa==fb) continue;
if((sensor[i].second+sensor[j].second)*(sensor[i].second+sensor[j].second)>=dist(sensor[i].first,sensor[j].first)){
root[fa] = fb;
}
}
for(int i = 1; i <= k; i++){
if(!mp.count(findx(i))) mp.insert(make_pair(findx(i),++tot));
SET[mp.at(findx(i))].emplace_back(i);
}
bool ok = true;
for(int i = 1; i <= tot; i++){
int u = -INF, d = INF, l = INF, r = -INF;
for(auto p : SET[i]){
u = max(u,sensor[p].first.second+sensor[p].second);
d = min(d,sensor[p].first.second-sensor[p].second);
l = min(l,sensor[p].first.first-sensor[p].second);
r = max(r,sensor[p].first.first+sensor[p].second);
}
if((u>=m||l<=0)&&(d<=0||r>=n)){
ok = false;
break;
}
}
puts(ok?"S":"N");
return 0;
}
\(B.Buffoon\)
签到
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+10;
int a[N],n,maxi;
int main(){
cin>>n;
for(int i=1;i<=n;++i) cin >> a[i], maxi = max(maxi,a[i]);
if(maxi==a[1]) cout << "S";
else cout << "N";
return 0;
}
\(C.Crossings\ With\ Danger\)
\(D.Denouncing Mafia\)
树形DP+优先队列 对于每个节点记录它的最深节点的位置，把链长为关键字丢到优先队列中，每次找最长的没有被遍历过的链
//#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<bits/stdc++.h>
using namespace std;
function<void(void)> ____ = [](){ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);};
const int MAXN = 1e5+7;
int n,m,par[MAXN],depth[MAXN],vis[MAXN];
vector<int> G[MAXN];
priority_queue<pair<int,pair<int,int>>,vector<pair<int,pair<int,int>>>,less<pair<int,pair<int,int>>>> que;
int dfs(int u){
depth[u] = depth[par[u]]+1;
int maxdep = u;
for(int v : G[u]){
int p = dfs(v);
maxdep = depth[maxdep]<depth[p]?p:maxdep;
}
que.push(make_pair(depth[maxdep]-depth[u]+1,make_pair(maxdep,u)));
return maxdep;
}
int main(){
scanf("%d %d",&n,&m);
for(int i = 2; i <= n; i++){
scanf("%d",&par[i]);
G[par[i]].emplace_back(i);
}
dfs(1);
int ans = 0;
while(!que.empty()&&m){
auto p = que.top();
que.pop();
if(vis[p.second.second]) continue;
m--;
ans += p.first;
while(p.second.first!=par[p.second.second]){
vis[p.second.first] = 1;
p.second.first = par[p.second.first];
}
}
printf("%d\n",ans);
return 0;
}
\(E.Exhibition\ of\ Clownfish\)
\(F.Forests\ in\ Danger\)
二分河流宽度，然后得到的矩形先和大矩形求交，再把所有矩形求面积并即可
//#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<bits/stdc++.h>
using namespace std;
function<void(void)> ____ = [](){ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);};
using LL = int_fast64_t;
const int MAXN = 1e5+7;
struct Rectangle{
int x1,y1,x2,y2;
Rectangle (int _x1 = 0, int _y1 = 0, int _x2 = 0, int _y2 = 0){
x1 = _x1; y1 = _y1;
x2 = _x2; y2 = _y2;
}
Rectangle intersect(const Rectangle &rhs){
int nx1 = max(x1,rhs.x1);
int ny1 = max(y1,rhs.y1);
int nx2 = min(x2,rhs.x2);
int ny2 = min(y2,rhs.y2);
return Rectangle(nx1,ny1,nx2,ny2);
}
}river[MAXN],Forest;
vector<pair<pair<int,int>,int> > line[MAXN];
int n,p;
struct SegmentTree{
int sz[MAXN<<2],cover[MAXN<<2],l[MAXN<<2],r[MAXN<<2];
#define ls(rt) rt << 1
#define rs(rt) rt << 1 | 1
void pushup(int rt){
if(l[rt]+1==r[rt]){
if(cover[rt]) sz[rt] = 1;
else sz[rt] = 0;
return;
}
if(cover[rt]) sz[rt] = r[rt] - l[rt];
else sz[rt] = sz[ls(rt)] + sz[rs(rt)];
}
void build(int L, int R, int rt){
l[rt] = L, r[rt] = R;
sz[rt] = cover[rt] = 0;
if(L+1==R) return;
int mid = (L+R) >> 1;
build(L,mid,ls(rt));
build(mid,R,rs(rt));
}
void update(int L, int R, int rt, int x){
if(l[rt]>=R || L>=r[rt]) return;
if(L<=l[rt] && r[rt]<=R){
cover[rt] += x;
pushup(rt);
return;
}
update(L,R,ls(rt),x);
update(L,R,rs(rt),x);
pushup(rt);
}
int query(){ return sz[1]; }
}ST;
bool check(int mid){
for(int i = 0; i < MAXN; i++) line[i].clear();
for(int i = 1; i <= n; i++){
Rectangle tp(river[i].x1-mid,river[i].y1-mid,river[i].x2+mid,river[i].y2+mid);
tp = tp.intersect(Forest);
line[tp.y1].emplace_back(make_pair(make_pair(tp.x1,tp.x2),1));
line[tp.y2].emplace_back(make_pair(make_pair(tp.x1,tp.x2),-1));
}
LL area = 0;
ST.build(0,Forest.x2+1,1);
for(int i = Forest.y1; i <= Forest.y2; i++){
area += ST.query();
for(auto p : line[i]) ST.update(p.first.first,p.first.second,1,p.second);
}
return area*100 >= (LL(Forest.x2)-Forest.x1)*(Forest.y2-Forest.y1)*p;
}
int solve(){
int l = 1, r = MAXN;
while(l<=r){
int mid = (l+r) >> 1;
if(check(mid)) r = mid - 1;
else l = mid + 1;
}
return l;
}
int main(){
scanf("%d",&n);
for(int i = 1; i <= n; i++){
scanf("%d %d %d %d",&river[i].x1,&river[i].y1,&river[i].x2,&river[i].y2);
if(river[i].x1>river[i].x2) swap(river[i].x1,river[i].x2);
if(river[i].y1>river[i].y2) swap(river[i].y1,river[i].y2);
}
scanf("%d",&p);
scanf("%d %d %d %d",&Forest.x1,&Forest.y1,&Forest.x2,&Forest.y2);
if(Forest.x1>Forest.x2) swap(Forest.x1,Forest.x2);
if(Forest.y1>Forest.y2) swap(Forest.y1,Forest.y2);
printf("%d\n",solve());
return 0;
}
\(G.Getting\ Confidence\)
将乘法变成对数的加法然后就是KM匹配的模板了
//#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<bits/stdc++.h>
using namespace std;
function<void(void)> ____ = [](){ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);};
const int MAXN = 111;
const int INF = 0x3f3f3f3f;
int n,LX[MAXN],LY[MAXN],visx[MAXN],visy[MAXN],match[MAXN],slack[MAXN],G[MAXN][MAXN];
bool dfs(int x){
visx[x] = 1;
for(int y = 1; y <= n; y++){
if(visy[y]) continue;
int gap = LX[x] + LY[y] - G[x][y];
if(!gap){
visy[y] = 1;
if(match[y]==-1||(!visx[match[y]]&&dfs(match[y]))){
match[y] = x;
return true;
}
}
else slack[y] = min(slack[y],gap);
}
return false;
}
void KM_match(){
memset(match,255,sizeof(match));
for(int i = 1; i <= n; i++) LX[i] = *max_element(G[i]+1,G[i]+1+n);
memset(LY,0,sizeof(LY));
for(int i = 1; i <= n; i++){
memset(slack,INF,sizeof(slack));
while(true){
memset(visx,0,sizeof(visx));
memset(visy,0,sizeof(visy));
if(dfs(i)) break;
int d = INF;
for(int j = 1; j <= n; j++) if(!visy[j]) d = min(d,slack[j]);
for(int j = 1; j <= n; j++) if(visx[j]) LX[j]-=d;
for(int j = 1; j <= n ;j++) if(visy[j]) LY[j]+=d;
else slack[j]-=d;
}
}
for(int i = 1; i <= n; i++) printf("%d ",match[i]);
}
int main(){
scanf("%d",&n);
for(int i = 1; i <= n; i++) for(int j = 1; j <= n; j++){
scanf("%d",&G[i][j]);
G[i][j] = log(G[i][j])*1000000;
}
KM_match();
puts("");
return 0;
}
\(H.Hour\ for\ a\ Run\)
签到
//#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<bits/stdc++.h>
using namespace std;
function<void(void)> ____ = [](){ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);};
int n,m;
int main(){
____();
cin >> n >> m;
for(int i = 1; i < 10; i++) cout << int(ceil((n*m*i)/10.0)) << ' '; cout << endl;
return 0;
}
\(I.Interplanetary\)
离线之后按顺序加点跑floyd
//#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<bits/stdc++.h>
using namespace std;
function<void(void)> ____ = [](){ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);};
const int MAXN = 1e5+7;
const int INF = 0x3f3f3f3f;
struct Query{
int u,v,k,id;
Query(){}
Query(int u, int v, int k, int id){
this->u = u;
this->v = v;
this->k = k;
this->id = id;
}
}Q[2][MAXN];
int n,m,qs,res[MAXN],temp[MAXN],initG[444][444],q[2],G[444][444];
void solve(){
vector<int> tmp(n),nodes(n);
for(int i = 0; i < n; i++){
tmp[i]=temp[i+1];
nodes[i]=i+1;
}
sort(tmp.begin(),tmp.end());
tmp.erase(unique(tmp.begin(),tmp.end()),tmp.end());
function<bool(int,int)> cmp[2] = {
[](int x, int y){ return temp[x] < temp[y]; },
[](int x, int y){ return temp[x] > temp[y]; }
};
for(int op = 0; op <= 1; op++){
for(int i = 1; i <= n; i++) for(int j = 1; j <= n; j++) G[i][j] = initG[i][j];
sort(nodes.begin(),nodes.end(),cmp[op]);
if(!op) sort(tmp.begin(),tmp.end(),less<int>());
else sort(tmp.begin(),tmp.end(),greater<int>());
sort(Q[op]+1,Q[op]+1+q[op],[](const Query &x, const Query &y){ return x.k < y.k; });
for(int i = 1, cur = 0; i <= q[op]; i++){
while(cur<n){
if((!op&&temp[nodes[cur]]>tmp[Q[op][i].k-1])||(op&&temp[nodes[cur]]<tmp[Q[op][i].k-1])) break;
int node = nodes[cur++];
for(int u = 1; u <= n; u++) for(int v = 1; v <= n; v++)
G[u][v] = G[v][u] = min(G[u][v],G[u][node]+G[node][v]);
}
int u = Q[op][i].u, v = Q[op][i].v, ID = Q[op][i].id;
res[ID] = G[u][v]==INF?-1:G[u][v];
}
}
}
int main(){
scanf("%d %d",&n,&m);
for(int i = 1; i <= n; i++) scanf("%d",&temp[i]);
memset(initG,INF,sizeof(initG));
for(int i = 1; i <= n; i++) initG[i][i] = 0;
for(int i = 1; i <= m; i++){
int u, v, d;
scanf("%d %d %d",&u,&v,&d);
initG[u][v] = initG[v][u] = d;
}
scanf("%d",&qs);
for(int i = 1; i <= qs; i++){
int u, v, k, op;
scanf("%d %d %d %d",&u,&v,&k,&op);
Q[op][++q[op]] = Query(u,v,k,i);
}
solve();
for(int i = 1; i <= qs; i++) printf("%d\n",res[i]);
return 0;
}
\(J.Jar\ of\ Water\ Game\)
按题意模拟即可
//#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<bits/stdc++.h>
using namespace std;
function<void(void)> ____ = [](){ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);};
int n,m;
int dec(char ch){
if(ch=='A') return 1;
else if(ch=='D') return 10;
else if(ch=='Q') return 11;
else if(ch=='J') return 12;
else if(ch=='K') return 13;
else return ch-'0';
}
struct P{
bool wildcard,tag;
vector<int> card;
int get(){
if(wildcard){
if(tag) tag = false;
else{
wildcard = false;
return -1;
}
}
map<int,int> cards;
for(int c : card) cards[c]++;
int minn = 6;
for(auto p : cards) minn = min(minn,p.second);
for(auto p : cards){
if(p.second!=minn) continue;
card.erase(find(card.begin(),card.end(),p.first));
return p.first;
}
}
void insert(int c){
if(c==-1) wildcard = tag = true;
else card.emplace_back(c);
}
}player[20];
bool check(int ID){
if(player[ID].wildcard) return false;
if(player[ID].card[0]!=player[ID].card[1]) return false;
if(player[ID].card[1]!=player[ID].card[2]) return false;
if(player[ID].card[2]!=player[ID].card[3]) return false;
return true;
}
int main(){
scanf("%d %d",&n,&m);
for(int i = 1; i <= n; i++){
char cd[10];
scanf("%s",cd);
player[i].card.resize(4);
for(int k = 0; k < 4; k++) player[i].card[k] = dec(cd[k]);
if(i==m) player[i].wildcard = player[i].tag = true;
else player[i].wildcard = player[i].tag = false;
}
for(int i = 1; i <= n; i++) if(check(i)) return printf("%d\n",i),0;
int now = m;
while(true){
int nxt = now+1==n+1?1:now+1;
player[nxt].insert(player[now].get());
if(check(now)) break;
now = nxt;
}
printf("%d\n",now);
return 0;
}
\(K.Keep\ Calm\ and\ Sell\ Balloons\)
矩阵快速幂，要找出递推公式
首先我们令\(f[n]\)表示\(2·n\)的矩阵从一个角开始走回到它垂直位置的方案数，可以发现\(f[n]=2·f[n-1], f[1]=1\)，即\(f[n]=2^{n-1}\)
现在我们定义\(g[n]\)为从矩阵的一个角开始走走完整个矩阵的方案数，模拟一下方案数可以找到递推式：\(g[n]=f[n]+2·g[n-1]+4·g[n-2]\)
即\(g[n]\ =\ 2·g[n-1]+4·g[n-2]+2^{n-1},g[0]=0,g[1]=1\)
\(f[n]\)容易得出，\(2·g[n-1]\)的情况在第一张图，\(4·g[n-2]\)的情况在第二张图
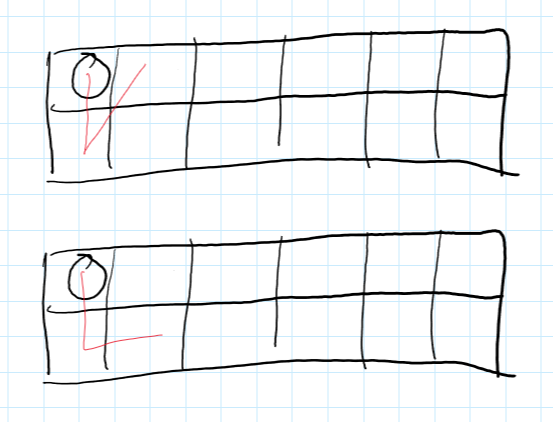
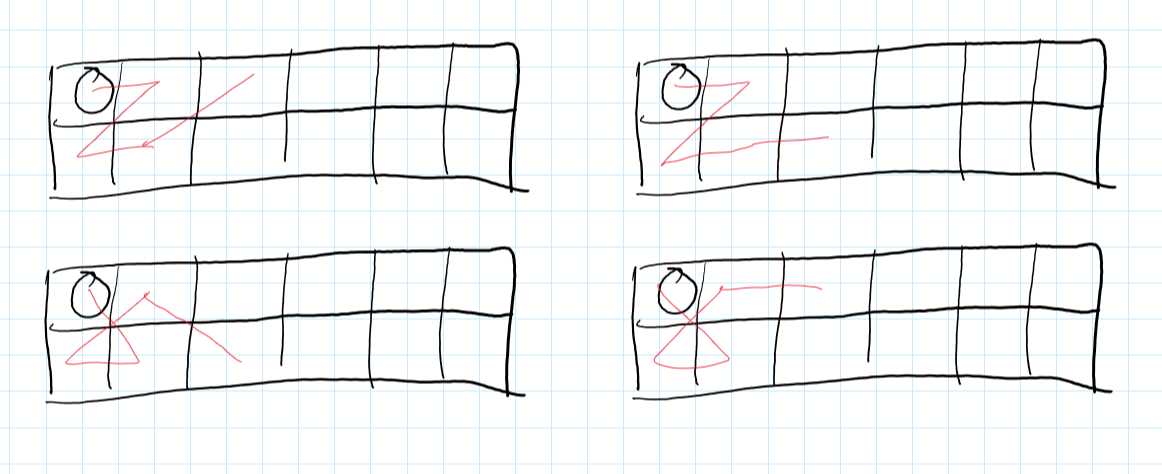
接下来我们定义\(h[n]\)为从矩阵的中间出发走完整个矩阵的方案数，可以把从中间出发走完整个矩阵分成两部分:
- 先从一边走回到垂直位置
- 再走完另一边
可以得到如下递推式：
\[h[n]=2·2·\sum^{n-1}_{k=2}2·f[k]·g[n-k]=\sum^{n-1}_{k=2}2^{k+2}·g[n-k]
\]
\]
其中第一个\(2\)是因为有上下两块，第二个\(2\)是因为可以先向右回到垂直位置再走完左边，也可以先向左回到垂直位置再走完右边，方案是对称的
\[h[n-1]=\sum^{n-2}_{k=2}2^{k+2}·g[n-1-k]
\]
\]
\[=\frac{\sum^{n-2}_{k=2}2^{k+3}·g[n-1-k]}{2}
\]
\]
\[=\frac{\sum^{n-1}_{k=3}2^{k+2}·g[n-k]}{2}
\]
\]
然后找一下\(h[n]\)和\(h[n-1]\)的关系
\[即:h[n]=2·h[n-1]+16·g[n-2],h[0]=h[1]=0
\]
\]
所以最后答案就是\(h[n]+4·g[n]\)
！注意啊要从\(2\)开始递推，\(g[2] \ne 2·g[1]+4·g[0]+f[2]\)
//#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<bits/stdc++.h>
using namespace std;
function<void(void)> ____ = [](){ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);};
using LL = int_fast64_t;
const LL MOD = 1e9+7;
struct Matrix{
LL m[6][6];
Matrix(int init = 1){
for(int i = 1; i <= 5; i++) for(int j = 1; j <= 5; j++){
if(i!=j) m[i][j] = 0;
else m[i][j] = init;
}
}
Matrix operator*(const Matrix rhs){
Matrix res(0);
for(int i = 1; i <= 5; i++){
for(int j = 1; j <= 5; j++){
for(int k = 1; k <= 5; k++)
res.m[i][j] = (res.m[i][j]+m[i][k]*rhs.m[k][j])%MOD;
}
}
return res;
}
Matrix operator*=(const Matrix rhs){
return *this = (*this)*rhs;
}
};
Matrix qpow(Matrix A, LL b){
Matrix res(1);
while(b){
if(b&1) res*=A;
b >>= 1;
A*=A;
}
return res;
}
LL n;
int main(){
scanf("%I64d",&n);
if(n==1) return puts("2"),0;
Matrix mat(0);
mat.m[1][1] = 2;
mat.m[1][3] = 16;
mat.m[2][2] = 2;
mat.m[2][3] = 4;
mat.m[2][4] = 2;
mat.m[3][2] = 1;
mat.m[4][4] = 2;
mat.m[5][5] = 1;
mat = qpow(mat,n-2);
printf("%I64d\n",(6*mat.m[1][2]+mat.m[1][3]+2*mat.m[1][4]+mat.m[1][5]+4*(6*mat.m[2][2]+mat.m[2][3]+2*mat.m[2][4]+mat.m[2][5]))%MOD);
return 0;
}
\(L.Less\ Coin\ Tosses\)
答案就是\(C(n,0)%2+C(n,1)%2+...+C(n,n-1)%2+C(n,n-1)%2\)
根据卢卡斯定理，答案就是2的\(N\)二进制位中1的个数次幂
//#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<bits/stdc++.h>
using namespace std;
function<void(void)> ____ = [](){ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);};
int_fast64_t n;
#define lowbit(x) ((x)&(-x))
int main(){
scanf("%I64d",&n);
int_fast64_t res = 1;
while(n) res <<= 1,n-=lowbit(n);
printf("%I64d\n",res);
return 0;
}
\(M.Maratona\ Brasileira\ de\ Popcorn\)
二分答案判定即可
//#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<bits/stdc++.h>
using namespace std;
function<void(void)> ____ = [](){ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);};
const int MAXN = 1e5+7;
using LL = int_fast64_t;
int n,c,t,A[MAXN];
bool check(int mid){
int cur = 0, tot = 1;
for(int i = 1; i <= n; i++){
if(mid*1ll*t<A[i]) return false;
if(mid*1ll*t>=cur+A[i]) cur+=A[i];
else{
tot++;
cur = A[i];
}
}
return tot<=c;
}
int solve(){
int l = 1, r = 1e9+7;
while(l<=r){
int mid = (l+r) >> 1;
if(check(mid)) r = mid - 1;
else l = mid + 1;
}
return l;
}
int main(){
scanf("%d %d %d",&n,&c,&t);
for(int i = 1; i <= n; i++) scanf("%d",&A[i]);
printf("%d\n",solve());
return 0;
}
2019-2020 ACM-ICPC Brazil Subregional Programming Contest (11/13)的更多相关文章
- (寒假GYM开黑)2018-2019 ACM-ICPC Brazil Subregional Programming Contest
layout: post title: 2018-2019 ACM-ICPC Brazil Subregional Programming Contest author: "luowenta ...
- 2018-2019 ACM-ICPC Brazil Subregional Programming Contest PART (10/13)
$$2018-2019 ACM-ICPC Brazil Subregional Programming Contest$$ \(A.Slackline\ Adventure\) \(B.Marbles ...
- 2018-2019 ACM-ICPC Brazil Subregional Programming Contest
A:留坑 B:二维sg函数,特判边界情况 //#pragma GCC optimize(2) //#pragma GCC optimize(3) //#pragma GCC optimize(4) / ...
- Gym.101908 Brazil Subregional Programming Contest(寒假自训第六场)
这几天睡眠时间都不太够,室友晚上太会折腾了,感觉有点累,所以昨天的题解也没写,看晚上能不能补起来. B . Marbles 题意:给定N组数(xi,yi),玩家轮流操作,每次玩家可以选择其中一组对其操 ...
- 2013-2014 ACM-ICPC Brazil Subregional Programming Contest 题解
[题目链接] 这场比赛题面英文都好长... ... A - Zero or One 模拟. #include <bits/stdc++.h> using namespace std; in ...
- ACM ICPC, JUST Collegiate Programming Contest (2018) Solution
A:Zero Array 题意:两种操作, 1 p v 将第p个位置的值改成v 2 查询最少的操作数使得所有数都变为0 操作为可以从原序列中选一个非0的数使得所有非0的数减去它,并且所有数不能 ...
- ACM ICPC, Amman Collegiate Programming Contest (2018) Solution
Solution A:Careful Thief 题意:给出n个区间,每个区间的每个位置的权值都是v,然后找长度为k的区间,使得这个区间的所有位置的权值加起来最大,输出最大权值, 所有区间不重叠 思路 ...
- Codeforces Gym101473 A.Zero or One (2013-2014 ACM-ICPC Brazil Subregional Programming Contest)
代码: #include<iostream> #include<cstring> #include<cstdio> #include<cmath> #i ...
- Codeforces Gym101473 F.Triangles-前缀和 (2013-2014 ACM-ICPC Brazil Subregional Programming Contest)
前缀和. 代码: 1 #include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 #include< ...
随机推荐
- oop的三大特性和传统dom如何渲染
OOP的三大特性是什么: 封装 :就是将一个类的使用和实现分开,只保留部分接口和方法与外部联系继承:子类自动继承其父级类中的属性和方法,并可以添加新的属性和方法或者对部分属性和方法进行重写.继承增加了 ...
- 基于B/S架构的在线考试系统的设计与实现
前言 这个是我的Web课程设计,用到的主要是JSP技术并使用了大量JSTL标签,所有代码已经上传到了我的Github仓库里,地址:https://github.com/quanbisen/online ...
- （十四）json、pickle与shelve模块
任何语言,都有自己的数据类型,那么不同的语言怎么找到一个通用的标准? 比如,后端用Python写的,前端是js,那么后端如果传一个dic字典给前端,前端肯定不认. 所以就有了序列化这个概念. 什么是序 ...
- 【Git】3、创建Git版本库、配置Git仓库用户邮箱信息
初识Git 文章目录 初识Git 1.创建Git版本库 认识.git 2.基础配置 2.1.查看配置信息 2.2.配置昵称邮箱信息 2.3.修改配置信息 1.通过命令行 2.通过修改配置文件. 修改全 ...
- 【MySQL】使用MySQL（连接、选择数据库、显示数据库和表信息）
第3章 使用MySQL 文章目录 第3章 使用MySQL 连接 选择数据库 了解数据库和表 小结 简单记录 - MySQL必知必会 - [英]Ben Forta 将学习如何连接和登录到MySQL,如何 ...
- C#数组的 Length 和 Count()
C#数组的 Length 和 Count() C# 数组中 Length 表示数组项的个数,是个属性.而 Count() 也是表示项的个数,是个方法,它的值和 Length 一样.但实际上严格地说, ...
- LeetCode590. N叉树的后序遍历
题目 1 class Solution { 2 public: 3 vector<int>ans; 4 vector<int> postorder(Node* root) { ...
- CTFHub - Web（六)
命令注入: 1.进入页面,测试127.0.0.1, 关键代码: <?php $res = FALSE; if (isset($_GET['ip']) && $_GET['ip'] ...
- 攻防世界 - Web（一）
baby_web: 1.根据题目提示,初始页面即为index,将1.php改为index.php,发现依然跳转成1.php,尝试修改抓包,出现如下回显, 2.在header中获取flag, flag: ...
- 04--Docker数据卷和数据卷容器
.为什么要使用数据卷: Docker容器产生的数据,如果不通过docker commit生成新的镜像,使得数据做为镜像的一部分保存下来,那么当容器删除后,数据自然也就没有了.为了能保存数据在docke ...