Lambert漫反射的BRDF
Lambert漫反射brdf=Albedo/pi。
推导:
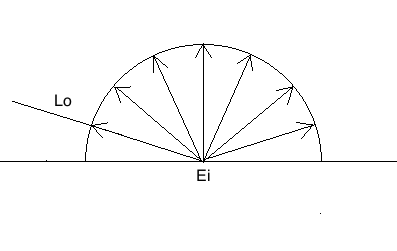
如图,设Lambert面元获得入射照度Ei,各方向均匀释放亮度,每个方向释放的亮度都是Lo。
又设此表面反射率为Albedo,根据反射率定义
Albedo=Eo/Ei
= (因为Lo各方向相同)=
(因为Lo各方向相同)= (
(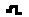 为半球)
为半球)
=(Lo*pi)/Ei
所以
brdf=Lo/Ei=Albedo/pi
注:
半球cos积分等于pi的计算过程:
作代换dw=sin(theta)*dtheta*dphi,则

或者也可以用直角坐标系来算,但比较繁:
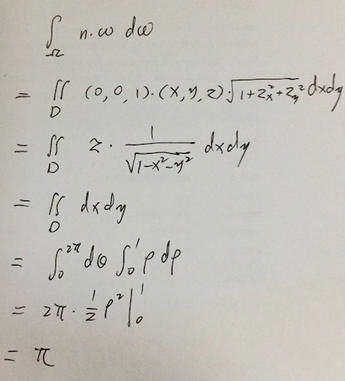
Lambert漫反射的BRDF的更多相关文章
- Lambert漫反射.BLinnPhong及Phong模型 Unity自带的在Lighting.cginc里
1.漫反射 此模型属于经验模型,主要用来简单模拟粗糙物体表面的光照现象 此模型假设物体表面为理想漫反射体(也就是只产生漫反射现象,也成为Lambert反射体),同时,场景中存在两种光,一种为环境光,一 ...
- pbr若干概念
pbr基于辐射传输理论,最基本的一个观点是:一切皆光源--任何一个面元既是光能接收器,也是光能发射器. 光通(flux):单位时间内通过某一面积的光能,单位W(瓦特),用表示. 可见,光通其实就是功率 ...
- 漫反射和Lambert模型
粗糙的物体表面向各个方向等强度地反射光,这种等同地向各个方向散射的现象称为光的漫反射(diffuse reflection).产生光的漫反射现象的物体表面称为理想漫反射体,也称为朗伯(Lambert) ...
- 【三】材质反射属性模型BRDF
双向反射分布函数(BRDF:Bidirecitonal Reflectance Distribution Function) 用来描述物体表面对光的反射性质 预备知识 BRDF的定义和性质 BRDF模 ...
- Microfacet模型采样下的brdf
本文前言 在学习图形学(games101 from bilibili)的时候,也遇到了像这样的问题,Cook-Torrance模型无法实现粗糙度为0时,物体微表面呈现绝对镜面的效果(呈现出一面镜子), ...
- Lambert模型
[Lambert模型] 漫反射光的强度近似地服从于Lambert定律,即漫反射光的光强仅与入射光的方向和反射点处表面法向夹角的余弦成正比. 由此可以构造出Lambert漫反射模型:Idiffuse = ...
- 精确光源(Punctual Light Sources)
<Physically-Based Shading Models in Film and Game Production>(SIGGRAPH 2010 Course Notes) (地址: ...
- Unity3D for VR 学习(9): Unity Shader 光照模型 (illumination model)
关于光照模型 所谓模型,一般是由学术算法发起, 经过大量实际数据验证而成的可靠公式 现在还记得2009年做TD-SCDMA移动通信算法的时候,曾经看过自由空间传播模型(Free space propa ...
- 由浅入深学习PBR的原理和实现
目录 一. 前言 1.1 本文动机 1.2 PBR知识体系 1.3 本文内容及特点 二. 初阶:PBR基本认知和应用 2.1 PBR的基本介绍 2.1.1 PBR概念 2.1.2 与物理渲染的差别 2 ...
随机推荐
- Compoer的应用
composer总结 composer常用命令 composer list 列出所有可用的命令composer init 初始化composer.json文件(就不劳我们自己费力创建啦),会要求输入一 ...
- 040 关于hive元数据的解析
一:原理 1.整体原理 找到数据库 找到表 先找分区表,然后不找SDS表了,先去找PARTITIONS表,根据这张表的SD_ID找对应的HDFS路劲 再普通表,直接根据SDS表的中SD_ID找到对应的 ...
- my作业
学号:2017xxxxxx 我是吴登峰,我的爱好是音乐,看电影,玩游戏! 我的码云个人主页是:https://gitee.com/fengaa 我的第一个项目地址是:https://gitee.com ...
- SpringMvc 文件下载 详解
最近SSM 需要用到文件下载,以前没用过,在百度上找了好久发现没有一篇博客,对于此段代码进行详细讲解, 这里是本人的个人总结,跟大家分享一下!!!不谢 /** * 文件下载 * ResponseEnt ...
- 线程、对称多处理和微内核(OS 笔记三)
线程.对称多处理 这一部分继续深入探讨与进程管理相关的高级概念并了解多处理机的对称多处理技术. 进程和线程 到目前为止提出的进程的概念包含两个特点: 资源所有权 存放进程映像的虚拟地址空间 调度/ ...
- 洛谷.2754.星际转移问题(最大流Dinic 分层)
题目链接 枚举时间 每一个时间点 对于每个之前的位置像当前位置连边,表示这一时刻可待在原地 每艘船 之前时刻位置向当前时刻连边 注意别漏了0时刻src连向earth的边 #include<cst ...
- BZOJ3861 : Tree
把集合看成左边的点,图中的点看成右边的点,若集合$i$不包含$j$,则连边$i->j$,得到一个二分图,等价于求这个二分图的完备匹配个数. 设$f[i][j]$表示考虑了前$i$个集合,匹配了$ ...
- Python和Mysql、Nginx
链接: python入门和基础: Python 中文学习大本营 你是如何自学 Python 的? 简明 Python 教程 给伸手党的福利:Python 新手入门引导 <Python爬虫学习系列 ...
- Chrome上网问题解决记录
浏览器打开网站缓慢,甚至等待很久后直接烂页面 注意观察浏览器左下角会显示: 正在建立安全连接... 环境: 操作系统:Win10 Chrome版本: 69.x 解决办法:http://bbs.360. ...
- Java实现字符串倒序输出的几种方法
1. 最容易想到的估计就是利用String类的toCharArray(),再倒序输出数组的方法了. import javax.swing.JOptionPane; public class Rever ...
