Python Algorithms – chapter2 基础知识

一、渐进记法

三个重要的记号

Ο、Ω、Θ，Ο记法表示渐进上界，Ω记法表示渐进下界，Θ记法同时提供了函数的上下界

几种常见的渐进运行时间实例

三种重要情况

最好的情况，最坏的情况，平均情况

最坏的情况通常是最有用的情况，可以对算法效率做出最佳保证

实证式算法评估

Tip1：If possible, don’t worry about it.

Tip2：用timeit模块进行计时

import timeit
timeit.timeit("x = 2+2") #0.003288868749876883
timeit.timeit("x = sum(range(10))") #0.003288868749897271

Tip3:用profiler找出瓶颈

使用cProfiler获取运行情况的内容，打印出程序中各函数的计时结果，如果python版本中没有cProfiler可以使用profiler代替

import cProfile
cProfile.run("helloworld()")

Tip4:绘制出结果

可以使用matplotlib绘制出结果，可参考http://www.cnblogs.com/huangqiancun/p/8379502.html

Tip5:在根据计时比对结果做出判断时要小心仔细

Tip6:通过相关实验对渐进时间做出判断时要小心仔细

二、图与树

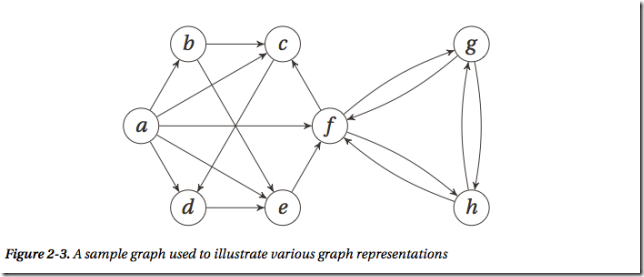
1 图的实现

邻接表

邻接集

a, b, c, d, e, f, g, h = range(8)
N = [
    {b, c, d, e, f},    # a
    {c, e},             # b
    {d},                # c
    {e},                # d
    {f},                # e
    {c, g, h},          # f
    {f, h},             # g
    {f, g}              # h
]

b in N[a] # True
len(N[f]) #

邻接列表

a, b, c, d, e, f, g, h = range(8)
N = [
    [b,c,d,e,f], #a
    [c,e], #b
    [d], #c
    [e], #d
    [f], #e
    [c,g,h], #f
    [f,h], #g
    [f,g] #h
    ]

加权邻接字典

a, b, c, d, e, f, g, h = range(8)
N = [
    {b:2, c:1, d:3, e:9, f:4},    # a
    {c:4, e:3},                   # b
    {d:8},                        # c
    {e:7},                        # d
    {f:5},                        # e
    {c:2, g:2, h:2},              # f
    {f:1, h:6},                   # g
    {f:9, g:8}                    # h
]

b in N[a] #  True
len(N[f]) #
N[a][b] #

邻接集的字典表示法

N = {
    'a': set('bcdef'),
    'b': set('ce'),
    'c': set('d'),
    'd': set('e'),
    'e': set('f'),
    'f': set('cgh'),
    'g': set('fh'),
    'h': set('fg')
}

邻接矩阵

a, b, c, d, e, f, g, h = range(8)
N = [[0,1,1,1,1,1,0,0], # a
     [0,0,1,0,1,0,0,0], # b
     [0,0,0,1,0,0,0,0], # c
     [0,0,0,0,1,0,0,0], # d
     [0,0,0,0,0,1,0,0], # e
     [0,0,1,0,0,0,1,1], # f
     [0,0,0,0,0,1,0,1], # g
     [0,0,0,0,0,1,1,0]] # h

N[a][b] # Neighborhood membership -> 1
sum(N[f]) # Degree -> 3

对不存在的边赋予无限大权值的加权矩阵

a, b, c, d, e, f, g, h = range(8)
_ = float('inf')

W = [[0,2,1,3,9,4,_,_], # a
     [_,0,4,_,3,_,_,_], # b
     [_,_,0,8,_,_,_,_], # c
     [_,_,_,0,7,_,_,_], # d
     [_,_,_,_,0,5,_,_], # e
     [_,_,2,_,_,0,2,2], # f
     [_,_,_,_,_,1,0,6], # g
     [_,_,_,_,_,9,8,0]] # h

W[a][b] < inf # True
sum(1 for w in W[a] if w < inf) - 1  #

注意：在对度值求和时务必要记得从中减1，因为我们不想把对角线也计算在内

Numpy库中的专用数组

N = [[0]*10 for i in range(10)]

import numpy as np
N = np.zeros([10,10])

更多内容可参考http://www.cnblogs.com/huangqiancun/p/8379241.html

2 树的实现

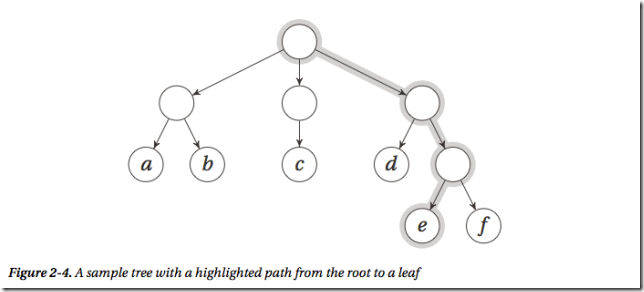
T = [["a", "b"], ["c"], ["d", ["e","f"]]]
T[0][1] # 'b'
T[2][1][0] # 'e'

二叉树类

class Tree:
    def __init__(self, left, right):
        self.left = left
        self.right = right

t = Tree(Tree("a", "b"), Tree("c", "d"))
t.right.left  # 'c'

多路搜索树类（左孩子，右兄弟）

class Tree:
    def __init__(self, kids, next=None):
        self.kids = self.val = kids
        self.next = next
return Tree

t = Tree(Tree("a", Tree("b", Tree("c", Tree("d")))))
t.kids.next.next.val  # 'c'

Bunch模式

bunch类

class Bunch(dict):
    def __init__(self, *args, **kwds):
        super(Bunch, self).__init__(*args, **kwds)
        self.__dict__ = self

x = Bunch(name = "Jayne Cobb", position = "Public Relations")
x.name #'Jayne Cobb'

T = Bunch
t = T(left = T(left = "a",right = "b"), right = T(left = "c"))
t.left # {'right': 'b', 'left': 'a'}
t.left.right #' b'
"left" in t.right # True

三、黑盒子

1 隐性平方级操作

from random import randrange
L = [randrange(10000) for i in range(1000)]
42 in L # False
S = set(L)
42 in S #False

看起来使用set毫无意义，但是成员查询在list中是线性级的，在set中则是常数级的

lists = [[1,2], [3,4,5], [6]]
sum(lists, []) #[1, 2, 3, 4, 5, 6]
res = []
for lst in lists:
    res.extend(lst)
# [1, 2, 3, 4, 5, 6]

sum函数是平方级的运行时间，第二个为更好的选择，当list的长度很短时，他们之间没有太大差距，但一旦超出某个长度，sum版本就会彻底完败

2 浮点运算的麻烦

sum(0.1 for i in range(10)) == 1.0 #False

def almost_equal(x, y, places=7):
    return round(abs(x-y), places) == 0

almost_equal(sum(0.1 for i in range(10)), 1.0) # True

from decimal import *
sum(Decimal("0.1") for i in range(10)) == Decimal("1.0") #True