机器学习之决策树（ID3）算法

最近刚把《机器学习实战》中的决策树过了一遍，接下来通过书中的实例，来温习决策树构造算法中的ID3算法。

海洋生物数据：

	不浮出水面是否可以生存	是否有脚蹼	属于鱼类
1	是	是	是
2	是	是	是
3	是	否	否
4	否	是	否
5	否	是	否

转换成数据集：

def createDataSet():
    dataSet = [[1, 1, 'yes'],
               [1, 1, 'yes'],
               [1, 0, 'no'],
               [0, 1, 'no'],
               [0, 1, 'no']]
    labels = ['no surfacing','flippers']
    return dataSet, labels

一、基础知识

1、熵

我把它简单的理解为用来度量数据的无序程度。数据越有序，熵值越低；数据越混乱或者分散，熵值越高。所以数据集分类后标签越统一，熵越低；标签越分散，熵越高。

更理论一点的解释：

熵被定义为信息的期望值，而如何理解信息？如果待分类的事物可能划分在多个分类中，则符号的信息定义为：

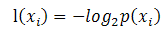
其中x_i是选择该分类的概率，即 该类别个数 / 总个数。

为了计算熵，我们需要计算所有类别所有可能值包含的信息期望值，公式如下：

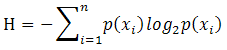其中n是分类的数目。

计算给定数据集的香农熵：

def calcShannonEnt(dataSet):
    numEntries = len(dataSet)
    #创建字典，计算每种标签对应的样本数
    labelCounts = {}

    for featVec in dataSet:
        currentLabel = featVec[-1]
        if currentLabel not in labelCounts.keys():
            labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1
    #根据上面的公式计算香农熵
    shannonEnt = 0.0
    for key in labelCounts:
        prob = float(labelCounts[key])/numEntries
        shannonEnt -= prob * log(prob,2)
    return shannonEnt

运行代码，数据集myDat1只有两个类别，myDat2有三个类别：

>>> myDat1

[[1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']]

>>> trees.calcShannonEnt(myDat1)

0.9709505944546686

>>> myDat2

[[1, 1, 'maybe'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']]

>>> trees.calcShannonEnt(myDat2)

1.3709505944546687

2、信息增益

信息增益可以衡量划分数据集前后数据（标签）向有序性发展的程度。

信息增益=原数据香农熵-划分数据集之后的新数据香农熵

二、按给定特征划分数据集

三个输入参数：待划分的数据集、划分数据集的特征位置、需要满足的当前特征的值

def splitDataSet(dataSet, axis, value):
    retDataSet = []
    for featVec in dataSet:
        if featVec[axis] == value:
            #获得除当前位置以外的特征元素
            reducedFeatVec = featVec[:axis]
            reducedFeatVec.extend(featVec[axis+1:])
            #把每个样本特征堆叠在一起，变成一个子集合
            retDataSet.append(reducedFeatVec)
    return retDataSet

运行结果：

>>> myDat

[[1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']]

>>> trees.splitDataSet(myDat,0,1)

[[1, 'yes'], [1, 'yes'], [0, 'no']]

>>> trees.splitDataSet(myDat,0,0)

[[1, 'no'], [1, 'no']]

三、选择最好的数据集划分方式，即选择出最合适的特征用于划分数据集

def chooseBestFeatureToSplit(dataSet):
    # 计算出数据集的特征个数
    numFeatures = len(dataSet[0]) – 1
    # 算出原始数据集的香农熵
    baseEntropy = calcShannonEnt(dataSet)
    bestInfoGain = 0.0; bestFeature = -1
    for i in range(numFeatures):
        # 抽取出数据集中所有第i个特征
        featList = [example[i] for example in dataSet]
        # 当前特征集合
        uniqueVals = set(featList)
        newEntropy = 0.0
        # 根据特征划分数据集，并计算出香农熵和信息增益
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet, i, value)
            prob = len(subDataSet)/float(len(dataSet))
            newEntropy += prob * calcShannonEnt(subDataSet)
        infoGain = baseEntropy - newEntropy

        # 返回最大信息增益的特征
        if(infoGain > bestInfoGain):
            bestInfoGain = infoGain
            bestFeature = i
    return bestFeature

四、如果数据集已经处理了所有特征属性，但是类标依然不是唯一的，此时采用多数表决的方式决定该叶子节点的分类。

def majorityCnt(classList):
    classCount={}
    for vote in classList:
        if vote not in classCount.keys(): classCount[vote] = 0
        classCount[vote] += 1
    sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)
return sortedClassCount[0][0]

五、创建决策树

接下来我们将利用上面学习的单元模块创建决策树。

def createTree(dataSet,labels):
    classList = [example[-1] for example in dataSet]
    # 如果划分的数据集只有一个类别，则返回此类别
    if classList.count(classList[0]) == len(classList):
        return classList[0]
    # 如果使用完所有特征属性之后，类别标签仍不唯一，则使用majorityCnt函数，多数表决法，哪种类别标签多，则分为此类别
    if len(dataSet[0]) == 1:
        return majorityCnt(classList)
    bestFeat = chooseBestFeatureToSplit(dataSet)
    bestFeatLabel = labels[bestFeat]
    myTree = {bestFeatLabel:{}}
    del(labels[bestFeat])
    featValues = [example[bestFeat] for example in dataSet]
    uniqueVals = set(featValues)
    for value in uniqueVals:
        subLabels = labels[:]
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels)
    return myTree

每次遇到递归问题总会头脑发昏，为了便于理解，我把一个创建决策树的处理过程重头到尾梳理了一遍。

原始数据集:

dataset: [[1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']]

labels: [no surfacing, flippers]

在调用createTree(dataSet,labels)函数之后，数据操作如下（每一个色块代表一次完整的createTree调用过程）：

1、

dataset: [[1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']]

labels: [no surfacing, flippers]

classList=['yes', 'yes', 'no', 'no', 'no']

选择最好的特征来分类：bestFeat= 0

bestFeatLabel =no surfacing

构造树：myTree {'no surfacing': {}}

去除这个特征后，label=['flippers']

这个特征（no surfacing）的值：featValues= [1, 1, 1, 0, 0]

特征类别 uniqueVals=[0, 1]

（1）类别值为0的时候：

子标签=['flippers']

分出的子集 splitDataSet(dataSet, bestFeat, value) = [[1, 'no'], [1, 'no']]

myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels)

1-1、

dataset: [[1, 'no'], [1, 'no']]

labels: ['flippers']

classList=['no', 'no']

满足classList中只有一个类别，返回no

myTree[bestFeatLabel][0] =’no’

myTree[bestFeatLabel] {0: 'no'}

也就是myTree {'no surfacing': {0: 'no'}}

（2）类别值为1的时候：

子标签=['flippers']

分出的子集 splitDataSet(dataSet, bestFeat, value) = [[1, 'yes'], [1, 'yes'], [0, 'no']]

myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels)

1-2、

dataset: [[1, 'yes'], [1, 'yes'], [0, 'no']]

labels: ['flippers']

classList=['yes', 'yes', 'no']

选择最好的特征来分类：bestFeat= 0

bestFeatLabel = flippers

构造树：myTree {'flippers': {}}

去除这个特征后，label=[]

这个特征（flippers）的值：featValues= [1, 1, 0]

特征类别 uniqueVals=[0, 1]

（1）类别值为0的时候：

子标签=[]

分出的子集 splitDataSet(dataSet, bestFeat, value) = [['no']]

myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels)

1-2-1、

dataset: [['no']]

labels: []

classList=['no']

满足classList中只有一个类别，返回no

myTree[bestFeatLabel][0] =’no’

myTree[bestFeatLabel] {0: 'no'}

也就是myTree {'flipper': {0: 'no'}}

（2）类别值为1的时候：

子标签=[]

分出的子集 splitDataSet(dataSet, bestFeat, value) = [['yes'], ['yes']]

myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels)

1-2-2、

dataset: [['yes'], ['yes']]

labels: []

classList=['yes', 'yes']

满足classList中只有一个类别，返回yes

myTree[bestFeatLabel][1] =’yes’

myTree[bestFeatLabel] {0: 'no', 1: 'yes'}

也就是myTree: {'flippers': {0: 'no', 1: 'yes'}}

myTree[bestFeatLabel][1] ={'flippers': {0: 'no', 1: 'yes'}}

myTree[bestFeatLabel] {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}

也就是myTree: {'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}}

例子中的决策树可视化图：

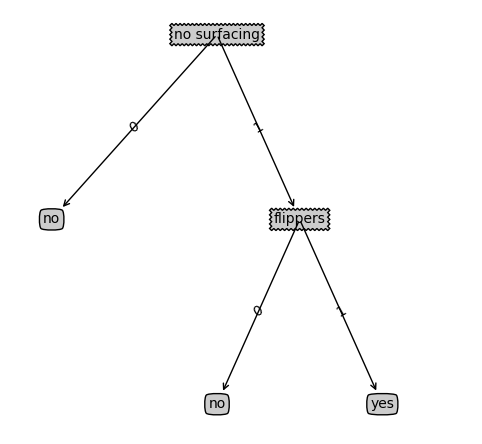
六、使用决策树做分类

def classify(inputTree, featLabels, testVec):
    firstStr = inputTree.keys()[0]
    secondDict = inputTree[firstStr]
    featIndex = featLabels.index(firstStr)
    for key in secondDict.keys():
        if testVec[featIndex] == key:
            if type(secondDict[key]).__name__=='dict':
                classLabel = classify(secondDict[key], featLabels, testVec)
            else: classLabel = secondDict[key]
    return classLabel

输出结果：

>>> myTree

{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}}

>>> labels

['no surfacing', 'flippers']

>>> trees.classify(myTree,labels,[1,0])

'no'

>>> trees.classify(myTree,labels,[1,1])

'yes'

七、 决策树的存储

构造决策树是很耗时的任务，然而用创建好的决策树解决分类问题，则可以很快的完成，可以通过使用pickle模块存储决策树。

def storeTree(inputTree, filename):
    import pickle
    fw = open(filename,'w')
    pickle.dump(inputTree,fw)
    fw.close()

def grabTree(filename):
    import pickle
    fr = open(filename)
    return pickle.load(fr)

---

参考资料：

[1] 《机器学习实战》

[2] 《机器学习实战》笔记——决策树（ID3）https://www.cnblogs.com/DianeSoHungry/p/7059104.html