工作流打包：

 
由于没有集成单点，配置文件要修改
将webnocas.xml内容复制覆盖 web.xml
 
到这里修改完毕 选择weblogic项目，右键maven install，生成.ear文件，打包完成。
 
 
打包完上传运行部署机器 192.168.22.52
用户名   bmsoft_yf
密码   ！@＃bmsoft123
路径：

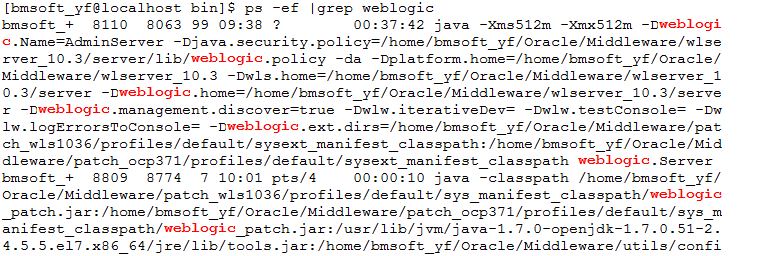
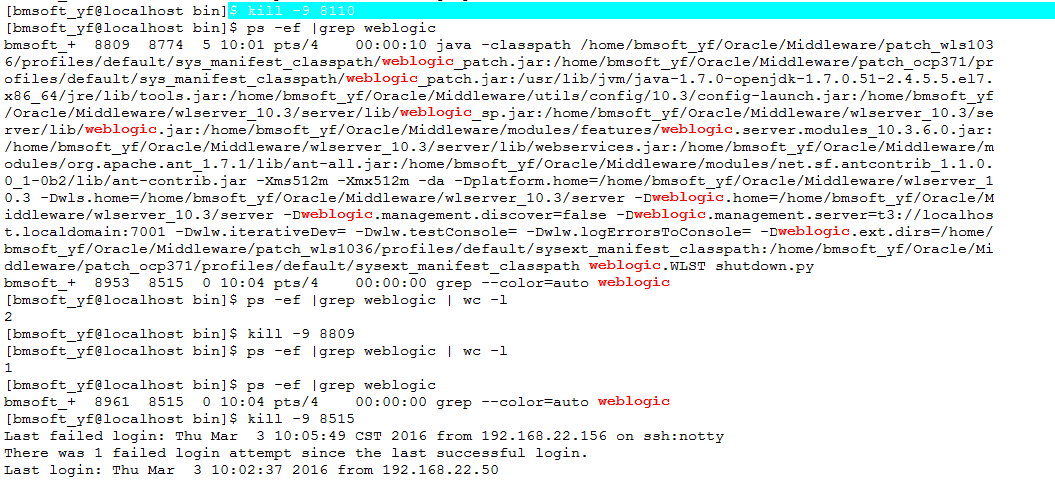
weblogic 部署

http://192.168.22.52:7001/console/

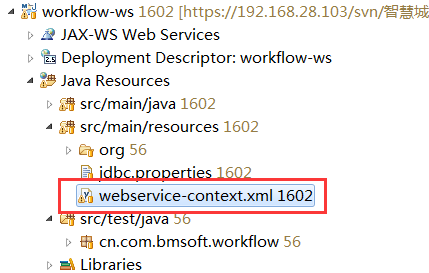
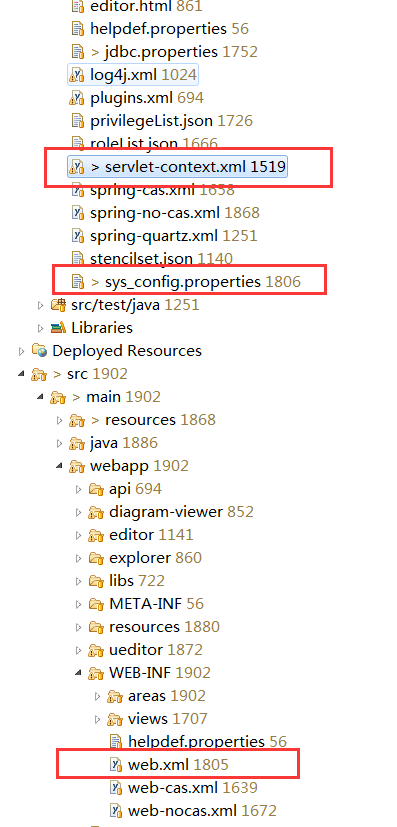
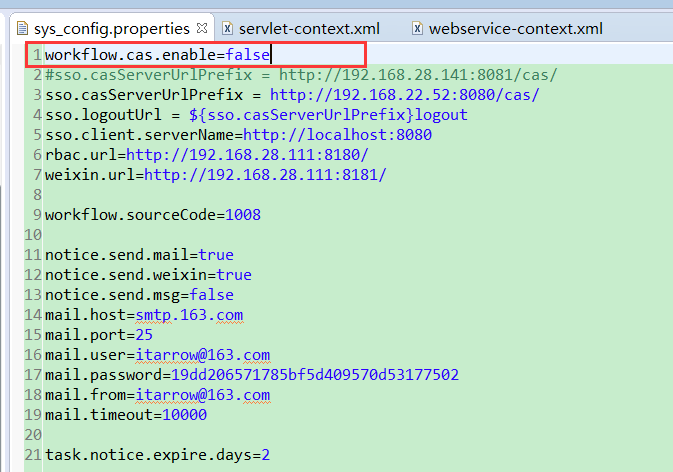
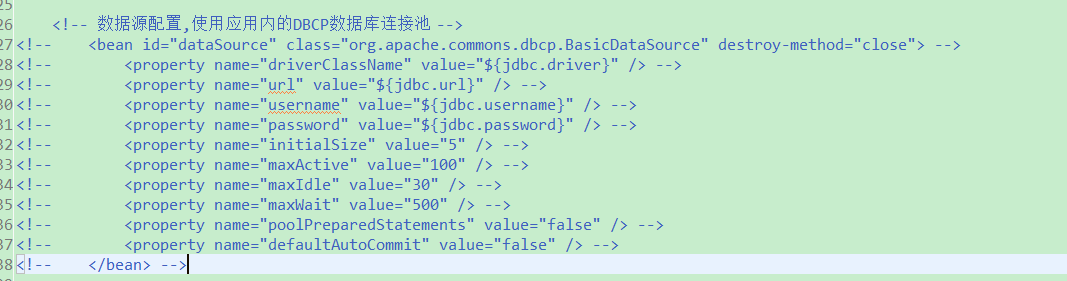
weblogic
china888
 
 
$ ps -ef |grep weblogic
 
 
 
$ kill -9 8110
$ ps -ef |grep weblogic
 

项目打包 weblogic部署的更多相关文章

  1. React项目打包并部署到 Github 展示预览效果

    React项目打包并部署到 Github 展示预览效果 当开发者模式结束,准备打包的时进行以下步骤: 在package.json配置文件中加一句: "homepage": &quo ...

  2. 项目打包 tomcat部署

    IDE: IDEA 1.项目maven管理先执行 clean,再执行 compile 2.如果编译compile不成功,则将 C:\Users\Administrator\.m2\repository ...

  3. idea maven项目打包并部署到tomcat

    打包 打开Maven管理器,邮寄package,执行Run Maven Build,执行成功后将war包生成到target目录下. 部署 1.将war包复制到tomcat安装目录下的webapps目录 ...

  4. Eclipse中创建新的SpringBoot项目(打包并且部署到tomcat)

    Spring-boot因为其对jar包的高度集成以及简化服务配置,快速部署等的优点,逐渐成为Java开发人员的热衷的框架.下面演示一下怎么在Eclipse中新建Spring-boot项目以及打包部署. ...

  5. 【Vue】基于nodejs的vue项目打包编译部署

    一·项目编译 1·进入项目目录下的终端执行命令 npm run build 正常情况如下图,如遇到错误不会编译成功,且编译后的html文件不能正常渲染. 2·编译完成后进入项目下的dist目录运行生成 ...

  6. vue之项目打包部署到服务器

    这是今年的第一篇博客.整理一下vue如何从项目打包到部署服务器,给大家做下分享,希望能给大家带来或多或少的帮助,喜欢的大佬们可以给个小赞,如果有问题也可以一起讨论下. 第一步:这是很关键的一步.打开项 ...

  7. 1.tomcat部署项目的几种方式和weblogic部署方式及一点通讯

      第一种部署方式: 直接使用myeclipse 找到server服务 添加要部署的项目Add Deployment ,然后选中某个项目,首选Exploded Archive(development ...

  8. 关于weblogic部署Java项目的包冲突问题

    我们可能会用各种应用服务部署我们的Java应用,比如Tomcat.WAS.weblogic等.Tomcat和WAS可能会比较少遇到一些奇怪的问题,但是用weblogic部署项目则经常遇到一些比如包冲突 ...

  9. Weblogic部署项目三种方式

    在weblogic中部署项目通常有三种方式:第一,在控制台中安装部署:第二,将部署包放在domain域中autodeploy目录下部署:第三,使用域中配置文件config.xml 进行项目的部署. 控 ...

随机推荐

  1. duilib入门简明教程 -- VS环境配置(2) Alberl

      既然是入门教程,那当然得基础点,因为搜索duilib相关资料时,发现有些小伙伴到处都是编译错误,以及路径配置错误等等,还有人不知道SVN,然后一个个文件手动下载的.     其实吧,duilib的 ...

  2. Nginx配置性能优化(转)

    大多数的Nginx安装指南告诉你如下基础知识——通过apt-get安装,修改这里或那里的几行配置,好了,你已经有了一个Web服务器了.而且,在大多数情况下,一个常规安装的nginx对你的网站来说已经能 ...

  3. android使用webview上传文件(支持相册和拍照)

    老夫最近需要做一个项目,需要调用服务器段的一些网页来选择文件,刚开始还挺纠结的,不知从何下手,网上大致预览了大神们走过的路,他们传统的方式都是使用一下代码: public void openFileC ...

  4. 【CF】310 Div.1 C. Case of Chocolate

    线段树的简单题目,做一个离散化,O(lgn)可以找到id.RE了一晚上,额,后来找到了原因. /* 555C */ #include <iostream> #include <str ...

  5. bzoj1042

    首先直接做多重背包肯定会TLE的, 观察这个背包问题有什么特殊性呢 物品种类和重量,价值是一定的,不同的是背包的容量和物品的数量 由于当物品数量没有限制的时候,方案数是可以预处理出来的 所以我们考虑用 ...

  6. 【http】

    var qs = require('querystring') require('http').createServer(function(req, res) { //res.writeHead(20 ...

  7. IE浏览器Ajax缓存问题小结

    IE浏览器Ajax缓存问题 在IE下使用ajax的get方法向后台请求数据时,如果请求URL与之前完全一样,则根本不想后台获取,直接返回上一次请求缓存的数据(在缓存过期之前,针对相同地址发起的多个Aj ...

  8. 【Android 复习】：第01期：引导界面（一）ViewPager介绍和使用详解

    一.ViewPager实现的效果图 二.ViewPager实现的功能 看到上面的效果图,想必大家已经猜出了这个类是干吗用的了,ViewPager类提供了多界面切换的新效果, 新效果有如下特征: < ...

  9. Ubuntu修改源

    linux里的源,简单理解就是你用 apt-get 命令去下载安装软件时,系统去哪里找这个软件.去的那个位置就是源. linux默认的源是国外的,下载速度比较慢,可以修改为国内的一些好的源地址,例如网 ...

  10. HW4.17

    import java.util.Scanner; public class Solution { public static void main(String[] args) { Scanner i ...