第五次编程作业-Regularized Linear Regression and Bias v.s. Variance
1.正规化的线性回归
(1)代价函数
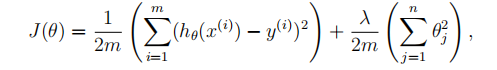
(2)梯度
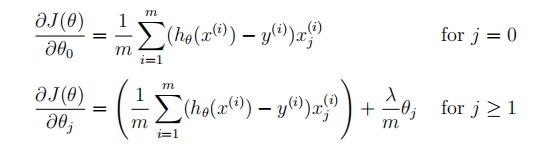
linearRegCostFunction.m
function [J, grad] = linearRegCostFunction(X, y, theta, lambda)
%LINEARREGCOSTFUNCTION Compute cost and gradient for regularized linear
%regression with multiple variables
% [J, grad] = LINEARREGCOSTFUNCTION(X, y, theta, lambda) computes the
% cost of using theta as the parameter for linear regression to fit the
% data points in X and y. Returns the cost in J and the gradient in grad % Initialize some useful values
m = length(y); % number of training examples % You need to return the following variables correctly
J = 0;
grad = zeros(size(theta)); % ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost and gradient of regularized linear
% regression for a particular choice of theta.
%
% You should set J to the cost and grad to the gradient.
%
%求h(θ)
h = X * theta;
J = 1/2/m *((h-y)'*(h-y)) + lambda/2/m*(theta(2:end,:)'*theta(2:end,:));
grad(1,1) = X(:,1)'*(h-y)/m;
grad(2:end,1) = X(:,2:end)'*(h-y)/m +lambda/m * theta(2:end,1);
% =========================================================================
grad = grad(:); end
用fmincg最优的theta来拟合线性回归,画出线性回归函数(在这里是低维度的可以画出来)
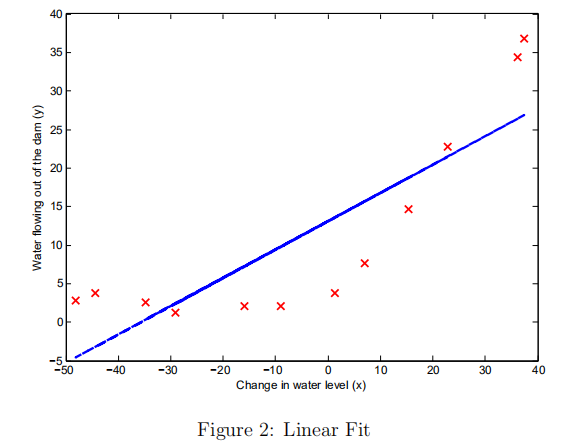
2.偏差与方差
(1)求训练样本的误差代价:
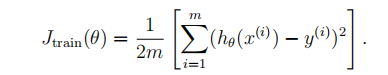
(2)交叉样本集
Jcv
learningCurve.m
function [error_train, error_val] = ...
learningCurve(X, y, Xval, yval, lambda)
%LEARNINGCURVE Generates the train and cross validation set errors needed
%to plot a learning curve
% [error_train, error_val] = ...
% LEARNINGCURVE(X, y, Xval, yval, lambda) returns the train and
% cross validation set errors for a learning curve. In particular,
% it returns two vectors of the same length - error_train and
% error_val. Then, error_train(i) contains the training error for
% i examples (and similarly for error_val(i)).
%
% In this function, you will compute the train and test errors for
% dataset sizes from 1 up to m. In practice, when working with larger
% datasets, you might want to do this in larger intervals.
% % Number of training examples
m = size(X, 1); % You need to return these values correctly
error_train = zeros(m, 1);
error_val = zeros(m, 1); % ====================== YOUR CODE HERE ======================
% Instructions: Fill in this function to return training errors in
% error_train and the cross validation errors in error_val.
% i.e., error_train(i) and
% error_val(i) should give you the errors
% obtained after training on i examples.
%
% Note: You should evaluate the training error on the first i training
% examples (i.e., X(1:i, :) and y(1:i)).
%
% For the cross-validation error, you should instead evaluate on
% the _entire_ cross validation set (Xval and yval).
%
% Note: If you are using your cost function (linearRegCostFunction)
% to compute the training and cross validation error, you should
% call the function with the lambda argument set to 0.
% Do note that you will still need to use lambda when running
% the training to obtain the theta parameters.
%
% Hint: You can loop over the examples with the following:
%
% for i = 1:m
% % Compute train/cross validation errors using training examples
% % X(1:i, :) and y(1:i), storing the result in
% % error_train(i) and error_val(i)
% ....
%
% end
% % ---------------------- Sample Solution ---------------------- %进行训练的时候,对训练样本i个进行训练得到theta值,再求J for i = 1:m
theta = trainLinearReg(X(1:i,:), y(1:i), lambda);
error_train(i) = linearRegCostFunction(X(1:i,:), y(1:i), theta, 0);
error_val(i) = linearRegCostFunction(Xval, yval,theta,0);
end % ------------------------------------------------------------- % ========================================================================= end
学习曲线如下:

3.多项式回归
(1) 上面学习曲线可以看出来高偏差,欠拟合。采用增加特性来拟合,即多项式如下:

polyFeatures.m
function [X_poly] = polyFeatures(X, p)
%POLYFEATURES Maps X (1D vector) into the p-th power
% [X_poly] = POLYFEATURES(X, p) takes a data matrix X (size m x 1) and
% maps each example into its polynomial features where
% X_poly(i, :) = [X(i) X(i).^2 X(i).^3 ... X(i).^p];
% % You need to return the following variables correctly.
X_poly = zeros(numel(X), p); % ====================== YOUR CODE HERE ======================
% Instructions: Given a vector X, return a matrix X_poly where the p-th
% column of X contains the values of X to the p-th power.
%
%
for i=1:p
X_poly(:,i) = X.^i;
end
% ========================================================================= end
(2) 画出学习曲线
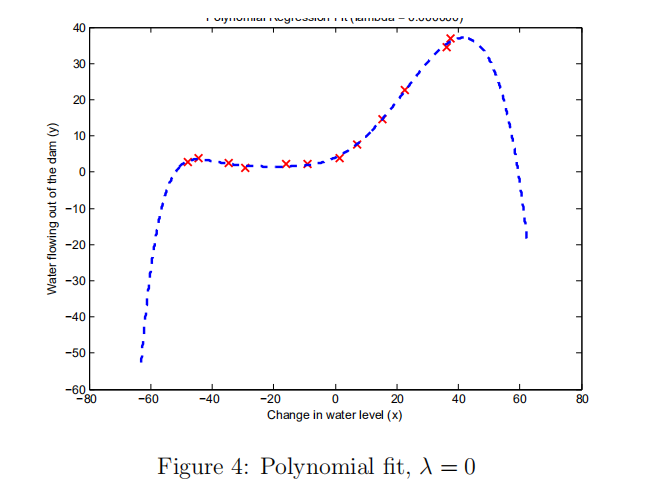
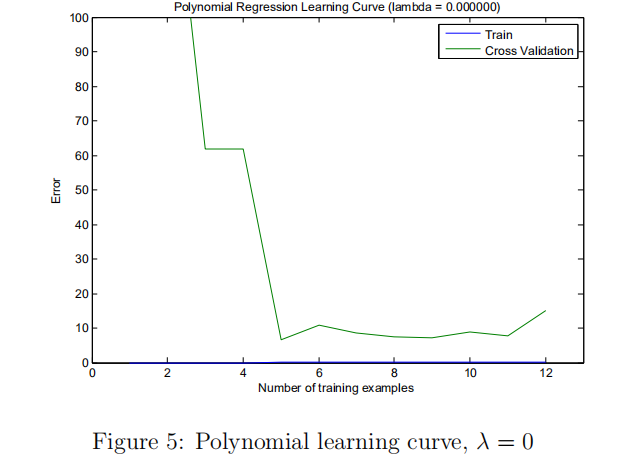
(2)可以看出出现了高方差,过拟合。选择一个好的正则化参数lambda。
利用交叉验证集来选择合适的lambda,选择最小的Jcv对应的lambda。(在这里求代价误差的时候就不用加正则化项了)
trainLinearReg.m
function [lambda_vec, error_train, error_val] = ...
validationCurve(X, y, Xval, yval)
%VALIDATIONCURVE Generate the train and validation errors needed to
%plot a validation curve that we can use to select lambda
% [lambda_vec, error_train, error_val] = ...
% VALIDATIONCURVE(X, y, Xval, yval) returns the train
% and validation errors (in error_train, error_val)
% for different values of lambda. You are given the training set (X,
% y) and validation set (Xval, yval).
% % Selected values of lambda (you should not change this)
lambda_vec = [0 0.001 0.003 0.01 0.03 0.1 0.3 1 3 10]'; % You need to return these variables correctly.
error_train = zeros(length(lambda_vec), 1);
error_val = zeros(length(lambda_vec), 1); % ====================== YOUR CODE HERE ======================
% Instructions: Fill in this function to return training errors in
% error_train and the validation errors in error_val. The
% vector lambda_vec contains the different lambda parameters
% to use for each calculation of the errors, i.e,
% error_train(i), and error_val(i) should give
% you the errors obtained after training with
% lambda = lambda_vec(i)
%
% Note: You can loop over lambda_vec with the following:
%
% for i = 1:length(lambda_vec)
% lambda = lambda_vec(i);
% % Compute train / val errors when training linear
% % regression with regularization parameter lambda
% % You should store the result in error_train(i)
% % and error_val(i)
% ....
%
% end
%
for i = 1:length(lambda_vec)
lambda = lambda_vec(i);
theta = trainLinearReg(X, y, lambda); %10x1选择最优的theta
error_train(i,1) = linearRegCostFunction(X, y, theta, 0);
error_val(i,1) = linearRegCostFunction(Xval, yval, theta, 0);
end % ========================================================================= end
(3)计算测试集代价误差3.8599,(根据上面得到的最优的λ= 3)
(4)画出学习曲线
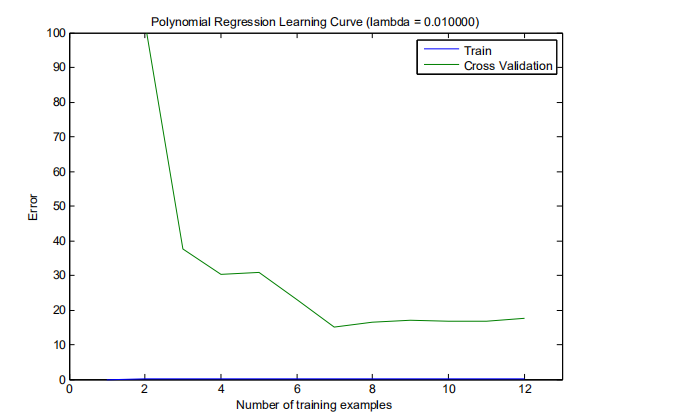
第五次编程作业-Regularized Linear Regression and Bias v.s. Variance的更多相关文章
- Andrew Ng机器学习 五:Regularized Linear Regression and Bias v.s. Variance
背景:实现一个线性回归模型,根据这个模型去预测一个水库的水位变化而流出的水量. 加载数据集ex5.data1后,数据集分为三部分: 1,训练集(training set)X与y: 2,交叉验证集(cr ...
- CheeseZH: Stanford University: Machine Learning Ex5:Regularized Linear Regression and Bias v.s. Variance
源码:https://github.com/cheesezhe/Coursera-Machine-Learning-Exercise/tree/master/ex5 Introduction: In ...
- Andrew Ng机器学习编程作业:Regularized Linear Regression and Bias/Variance
作业文件: machine-learning-ex5 1. 正则化线性回归 在本次练习的前半部分,我们将会正则化的线性回归模型来利用水库中水位的变化预测流出大坝的水量,后半部分我们对调试的学习算法进行 ...
- ufldl学习笔记与编程作业:Linear Regression(线性回归)
ufldl学习笔记与编程作业:Linear Regression(线性回归) ufldl出了新教程,感觉比之前的好.从基础讲起.系统清晰,又有编程实践. 在deep learning高质量群里面听一些 ...
- 【模式识别与机器学习】——PART2 机器学习——统计学习基础——Regularized Linear Regression
来源:https://www.cnblogs.com/jianxinzhou/p/4083921.html 1. The Problem of Overfitting (1) 还是来看预测房价的这个例 ...
- Regularized Linear Regression with scikit-learn
Regularized Linear Regression with scikit-learn Earlier we covered Ordinary Least Squares regression ...
- ufldl学习笔记和编程作业:Softmax Regression(softmax回报)
ufldl学习笔记与编程作业:Softmax Regression(softmax回归) ufldl出了新教程.感觉比之前的好,从基础讲起.系统清晰,又有编程实践. 在deep learning高质量 ...
- ufldl学习笔记与编程作业:Softmax Regression(vectorization加速)
ufldl学习笔记与编程作业:Softmax Regression(vectorization加速) ufldl出了新教程,感觉比之前的好.从基础讲起.系统清晰,又有编程实践. 在deep learn ...
- ufldl学习笔记与编程作业:Logistic Regression(逻辑回归)
ufldl学习笔记与编程作业:Logistic Regression(逻辑回归) ufldl出了新教程,感觉比之前的好,从基础讲起.系统清晰,又有编程实践. 在deep learning高质量群里面听 ...
随机推荐
- type显示的是访问类型,是较为重要的一个指标,结果值从好到坏依次是: system > const > eq_ref > ref > fulltext > ref_or_null > index_merge > unique_subquery > index_subquery > range > index > ALL ,一般来说,得保证查询至少达到range级别,最好能达到ref。 作者:高
MySQL EXPLAIN详解 - 简书 https://www.jianshu.com/p/ea3fc71fdc45 type显示的是访问类型,是较为重要的一个指标,结果值从好到坏依次是: syst ...
- vue 实现子向父传值
父组件 <template> <div id="app"> <child @onChange='onChildValue'></child ...
- poj1416
#include<iostream> using namespace std; int target,datanum; ],temproad[]; int N,flag,maxsum; ] ...
- LeetCode 705 Design HashSet 解题报告
题目要求 Design a HashSet without using any built-in hash table libraries. To be specific, your design s ...
- jmeter连接oracle时未找到要求的 FROM 关键字问题
1.jmeter的lib目录下已添加了JDBC连接oracle的驱动: 2.已在测试计划中添加了驱动文件 3.JDBC Connection Configuration配置如图 3.JDBC Requ ...
- Django中cookie和session使用
cookie和session的简单使用 def cookie(request): """ 操作cookie """ resp = HttpR ...
- springboot读取application.properties中自定义配置
假设在application-xxx.properties中配置 user.name=yuhk 一.在Controller中读取 @Value("{$user.name}") pr ...
- Redis Sentinel实现的机制与原理详解
序言 Redis-Sentinel是Redis官方推荐的高可用性(HA)解决方案.实际上这意味着你可以使用Sentinel模式创建一个可以不用人为干预而应对各种故障的Redis部署. 它的主要功能有以 ...
- javascript的ES6学习总结(第一部分)
ES6(ESNext学习总结——第一部分) ES6, 全称 ECMAScript 6.0 ,是 JavaScript 的下一个版本标准,2015.06 发版. ECMA每年6月份,发布一个版本 201 ...
- 【Linux】Mac PD set centos static ip
2,修改Centos的网络设置. (1)进入脚本. vi /etc/sysconfig/network-scripts/ifcfg-eth0 My Mac ip: # 从dhcp改成static BO ...
