8.10-Day1T2圈（circle）

圈（circle）

题目大意

一开始看这道题，觉得有点像备用钥匙那道题，需要离散化，

把一个球的两个点分开看...

但是..其中的规律我推不出来

（不是很难，只是蒟蒻好久都没有自己独立思考了）

题解

题解给的是离散化+线段树...
有一点点麻烦

看到其他轻松切题的大佬的代码

但关键部分的思想都是一样的

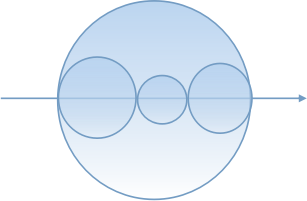
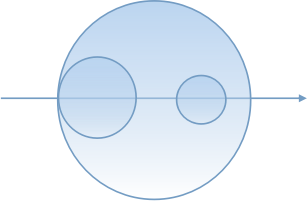
如果一个圆被其他圆完全分割，则这个圆增加的块数为2，否则为1

将所有圆按左端点从小到大排序，如果相同的话，就再按右端点从小到大排序

那么遍历圆，如果它的左右两个点都没有或者有一个没有被遍历到的话，将其加入到map中

如果都有被遍历到的话，那么他外面一定套着一个大的圆（于是当我这篇博客的时候我发现了问题...这个想法是错误的...我还是把它说完吧）对答案的贡献就+1。

#include<bits/stdc++.h>
#define ll long long
using namespace std;

inline int read()
{
    int sum = ,p = ;
    char ch = getchar();
    while(ch < '' || ch > '')
    {
        if(ch == '-')
            p = -;
        ch = getchar();
    }
    while(ch >= '' && ch <= '')
    {
        (sum *= ) += ch - '';
        ch = getchar();
    }
    return sum * p;
}

const int N = ;
map<int,bool>p;
ll ans,n;
struct node
{
    int l, r;
} e[N];
bool cmp(node x, node y)
{
    if(x.l != y.l)
        return x.l < y.l;
    else
        return x.r < x.r;
}
int main()
{
    freopen("circle.in","r",stdin);
    freopen("circle.out","w",stdout);
    n = read();
    ans = n + ;
    for(int i = ; i <= n; i++)
    {
        int x = read(),r = read();
        e[i].r = x + r;
        e[i].l = x - r;
    }
    sort(e + ,e + n + ,cmp);
    for(int i = ; i <= n; i++)
    {
        if(p[e[i].l] && p[e[i].r])
            ans++;
        else
            p[e[i].l] = p[e[i].r] = ;
    }
    printf("%lld\n", ans);
    return ;
}

错误算法

hack数据：3 0 20 0 10 15 5

还是安安心心看std吧

在所有圆中，如果一个圆的半径小于等于另一个圆的半径则这个圆不会包含另一个圆

所以按圆的半径由小到大排序则前面的圆只能只能被后面的圆包含。因此只需统计当前的圆是否被前面的圆覆盖。

因此先统计所有可能的区间将所有的点离散化，用线段数统计所有区间。每统计到下一个圆，先计算当前圆所包含的所有区间是否被完全覆盖。如果被完全覆盖，则答案+2。否则答案+1，然后将当前圆所包含的区间在线段树上标记。

时间复杂度 O（ N log(N)）。

注意最后答案需要+1（最大区间）。

（好好好麻烦...）

#include<stdio.h>
#include<algorithm>
using namespace std;
int n;
struct cir
{
    int r,pos;
}a[];
int has[],tmp[];
int cnt,ans;
int sum[];
int cmp(cir x,cir y)
{
    return x.r<y.r;
}
void pushup(int x)
{
    sum[x]=sum[x*]&sum[x*+];
}
void pushdown(int x)
{
    sum[x*]|=sum[x];
    sum[x*+]|=sum[x];
}
void insert(int lq,int rq,int ln,int rn,int now)
{
    if(has[ln]>=lq&&has[rn+]<=rq)
    {
        sum[now]=;
        return;
    }
    int mid=(ln+rn)>>;
    if(has[mid]>=lq)
    insert(lq,rq,ln,mid,now*);
    if(has[mid+]<rq)
    insert(lq,rq,mid+,rn,now*+);
    pushup(now);
}
int query(int lq,int rq,int ln,int rn,int now)
{
    if(has[ln]>=lq&&has[rn+]<=rq)
    return sum[now];
    pushdown(now);
    int mid=(ln+rn)>>;
    int ret=;
    if(has[mid]>=lq)
    ret&=query(lq,rq,ln,mid,now*);
    if(has[mid+]<rq)
    ret&=query(lq,rq,mid+,rn,now*+);
    return ret;
}
int main()
{
//    freopen("circle.in","r",stdin);
//    freopen("circle.out","w",stdout);
    scanf("%d",&n);
    for(int i=;i<=n;i++)
    {
        scanf("%d%d",&a[i].pos,&a[i].r);
        tmp[i*-]=a[i].pos-a[i].r;
        tmp[i*]=a[i].pos+a[i].r;
    }
    sort(tmp+,tmp++*n);
    for(int i=;i<=*n;i++)
    {
        if(tmp[i]!=tmp[i-]||i==)
        has[++cnt]=tmp[i];
    }
    sort(a+,a++n,cmp);
    for(int i=;i<=n;i++)
    {
        ans++;
        if(query(a[i].pos-a[i].r,a[i].pos+a[i].r,,cnt-,))
        ans++;
        insert(a[i].pos-a[i].r,a[i].pos+a[i].r,,cnt-,);
    }
    printf("%d",ans+);
}

幸福快乐std