秒懂机器学习---分类回归树CART

一、总结

一句话总结：

用决策树来模拟分类和预测，那些人还真是聪明：其实也还好吧，都精通的话想一想，混一混就好了

用决策树模拟分类和预测的过程：就是对集合进行归类的过程（归类自然也就给出了预测，因为某类的结果一般是一样的）

1、CART（ Classification And Regression Tree）算法是什么？

分类回归树算法

决策树的一种实现

2、CART（ Classification And Regression Tree）算法的实质是什么？

二分·递归·分割技术

CART算法是一种二分递归分割技术，把当前样本划分为两个子样本，使得生成的每个非叶子结点都有两个分支，因此CART算法生成的决策树是结构简洁的二叉树。由于CART算法构成的是一个二叉树，它在每一步的决策时只能为“是”或者“否”，即使一个feature有多个取值，也是把数据分为两部分。

3、通常决策树主要有哪三种实现？

ID3算法

CART算法

C4.5算法

4、在CART算法中主要的两个步骤是什么？

（1）决策树生成（决策树要尽量大）：将样本递归划分进行建树过程，生成的决策树要尽量大；

（2）决策树剪枝（使损失函数最小）：用验证数据进行剪枝，这时损失函数最小作为剪枝的标准。

5、CART算法的适用情况是什么？

分类和回归：CART既可以用于分类也可以用于回归

6、CART算法的算法流程是什么？

1、计算Gini系数 + 二分分割样本

2、选择Gini系数最小的特征及其对应的切分点作为最优特征与最优切分点

3、递归调用1、2

1、设结点的训练数据集为D,计算现有特征对该数据集的Gini系数，此时，对每一个特征A,对其可能取的每个值a，根据样本点对A=a的测试为“是”或“否”将D分割成D_{1}和D_{2}两部分，计算A=a时的Gini系数。

2、在所有可能的特征A以及它们所有可能的切分点a中，选择Gini系数最小的特征及其对应的切分点作为最优特征与最优切分点，依最优特征与最优切分点，从先结点生成两个子结点，将训练数据集依特征分配到两个子结点中去。

3、对两个子结点递归地调用步骤1-2，直至满足停止条件。

4、生成CART决策树。

算法停止计算的条件是结点中的样本个数小于预定阈值，或样本集的Gini系数小于预定阈值（样本基本属于同一类），或者没有更多特征。

7、CART算法的停止计算的条件是什么？

结点中的样本个数小于预定阈值

样本集的Gini系数小于预定阈值

没有更多特征

算法停止计算的条件是结点中的样本个数小于预定阈值，或样本集的Gini系数小于预定阈值（样本基本属于同一类），或者没有更多特征。

8、GINI指数是什么？

1、是一种不等性度量；

2、通常用来度量收入不平衡，可以用来度量任何不均匀分布；

3、是介于0~1之间的数，0-完全相等，1-完全不相等；

4、总体内包含的类别越杂乱，GINI指数就越大（跟熵的概念很相似）

9、为什么决策树需要剪枝？

决策树很容易发生过拟合，也就是由于对train数据集适应得太好，反而在test数据集上表现得不好。

10、剪枝常用思路有哪些？

1：使用训练集合(Training Set）和验证集合(Validation Set)，来评估剪枝方法在修剪结点上的效用

2：使用所有的训练集合进行训练，但是用统计测试来估计修剪特定结点是否会改善训练集合外的数据的评估性能，如使用Chi-Square（Quinlan，1986）测试来进一步扩展结点是否能改善整个分类数据的性能，还是仅仅改善了当前训练集合数据上的性能。

3：使用明确的标准来衡量训练样例和决策树的复杂度，当编码长度最小时，停止树增长，如MDL(Minimum Description Length)准则。

二、机器学习十大算法之CART

转自或参考：机器学习十大算法之CART
https://blog.csdn.net/qq_33273962/article/details/83818353

一、概述

CART（ Classification And Regression Tree）即分类回归树算法，它是决策树的一种实现，通常决策树主要有三种实现，分别是ID3算法，CART算法和C4.5算法。CART算法是一种二分递归分割技术，把当前样本划分为两个子样本，使得生成的每个非叶子结点都有两个分支，因此CART算法生成的决策树是结构简洁的二叉树。由于CART算法构成的是一个二叉树，它在每一步的决策时只能为“是”或者“否”，即使一个feature有多个取值，也是把数据分为两部分。在CART算法中主要分为两个步骤：

（1）决策树生成：将样本递归划分进行建树过程，生成的决策树要尽量大；

（2）决策树剪枝：用验证数据进行剪枝，这时损失函数最小作为剪枝的标准。

二、算法流程

CART决策树的生成就是递归地构建二叉树的过程，CART既可以用于分类也可以用于回归，这里我们对分类进行讨论，对分类而言，CART用Gini系数最小化准则来进行特征选择，生成二叉树。CART算法如下：

输入：训练数据集D，停止计算的条件；

输出：CART决策树。

根据训练数据集，从根结点开始递归地对每个节点进行一下操作，构建二叉决策树：

1、设结点的训练数据集为D,计算现有特征对该数据集的Gini系数，此时，对每一个特征A,对其可能取的每个值a，根据样本点对A=a的测试为“是”或“否”将D分割成 $D_{1}$ 和 $D_{2}$ 两部分，计算A=a时的Gini系数。

2、在所有可能的特征A以及它们所有可能的切分点a中，选择Gini系数最小的特征及其对应的切分点作为最优特征与最优切分点，依最优特征与最优切分点，从先结点生成两个子结点，将训练数据集依特征分配到两个子结点中去。

3、对两个子结点递归地调用步骤1-2，直至满足停止条件。

4、生成CART决策树。

算法停止计算的条件是结点中的样本个数小于预定阈值，或样本集的Gini系数小于预定阈值（样本基本属于同一类），或者没有更多特征。我们对Gini系数做简单介绍：

GINI指数：
1、是一种不等性度量；
2、通常用来度量收入不平衡，可以用来度量任何不均匀分布；
3、是介于0~1之间的数，0-完全相等，1-完全不相等；
4、总体内包含的类别越杂乱，GINI指数就越大（跟熵的概念很相似）

分类问题中，假设有 K 个类，样本属于第 k 类的概率为 pk，则概率分布的基尼指数为：

样本集合 D 的基尼指数为：

其中 Ck 为数据集 D 中属于第 k 类的样本子集。

如果数据集 D 根据特征 A 在某一取值 a 上进行分割，得到 D1 ，D2 两部分后，那么在特征 A 下集合 D 的基尼指数为：

具体算法流程如下面的例子：

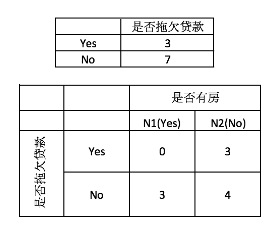
首先对数据集非类标号属性{是否有房，婚姻状况，年收入}分别计算他们的Gini系数增益，取Gini系数增益值最大的属性作为决策树的根结点属性。根结点的Gini系数：

当根据是否有房来进行划分时，Gini系数增益计算过程为

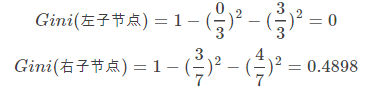
若按照婚姻状况来划分，属性婚姻状况有三个可能的取值{married,single,divorced}，分别计算划分后的

{married}|{single,divorced}

{single}|{married,divorced}

{devorced}|{single,married}的Gini系数

当分组为{married}|{single,divorced}时， $S_{l}$ 表示婚姻状况取值为married的分组， $S_{r}$ 表示婚姻状况取值为single或者divorced的分组

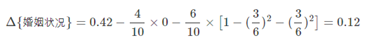
当分组为 {single}|{married,divorced}时，

当分组为{devorced}|{single,married}时，

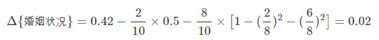
最后考虑年收入属性，我们发现它是一个连续的数值类型。对于年收入属性为数值型属性，首先需要对数据按升序排序，然后从小到大一次用相邻值的中间值作为分割将样本划分为两组。例如当面对年收入为60和70这两个值时，我们计算中间值为65。倘若以中间值65作为分割点， $S_{l}$ 作为年收入小于65的样本， $S_{r}$ 表示年收入大于等于65的样本，于是则有Gini系数增益为

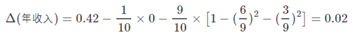
其他值的计算同理，下面列出计算结果如下（我们取其中使增益最大化的那个二分准则作为构建二叉树的准则）：

同样，我们计算剩下的属性，其中根结点的Gini系数为

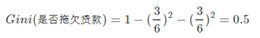
和前面的计算过程类似，对是否有房，可得

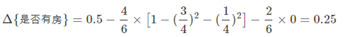
对于年收入属性则有

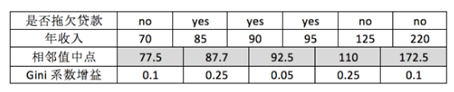
三、剪枝

决策树很容易发生过拟合，也就是由于对train数据集适应得太好，反而在test数据集上表现得不好。这个时候我们要么是通过阈值控制终止条件避免树形结构分支过细，要么就是通过对已经形成的决策树进行剪枝来避免过拟合。另外一个克服过拟合的手段就是基于Bootstrap的思想建立随机森林（Random Forest）。

先剪枝:在构造过程中，当某个节点满足剪枝条件，则直接停止此分支的构造。

后剪枝:先构造完成完整的决策树，再通过某些条件遍历树进行剪枝。

其实剪枝的准则是如何确定决策树的规模，可以参考的剪枝思路有以下几个：
：使用训练集合(Training Set）和验证集合(Validation Set)，来评估剪枝方法在修剪结点上的效用
：使用所有的训练集合进行训练，但是用统计测试来估计修剪特定结点是否会改善训练集合外的数据的评估性能，如使用Chi-Square（Quinlan，）测试来进一步扩展结点是否能改善整个分类数据的性能，还是仅仅改善了当前训练集合数据上的性能。
：使用明确的标准来衡量训练样例和决策树的复杂度，当编码长度最小时，停止树增长，如MDL(Minimum Description Length)准则。

参考：

https://blog.csdn.net/ACdreamers/article/details/44664481

https://blog.csdn.net/hewei0241/article/details/8280490

https://www.jianshu.com/p/b90a9ce05b28