UVa 623 大整数乘法

UVa 623

计算N！

n上限为1000自然不能直接算。所以可以开一个数组f[]，f[]每一位存N!结果的6位。如果按进制来理解，就是10^6进制：

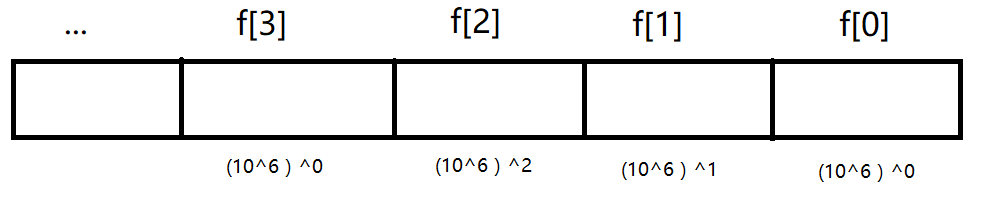
例如 11！=39916800=11*10！=11*(3628800)=11*(3*(10^6)^1+628800*(10^6)^0)

11*628800=6916800=6*(10^6)^1+916800*(10^6)^0,

所以上式进位为6，可得 11!=(11*3+6)*(1^10)^1+916800*(10^6)^0=39916800 ，如下图

输出时高位的前导0用printf("%06d")前面的0表示输出6位，不足6位前面补零。简直完美！

参考代码：

 #include<cstdio>
 #include<cstring>
 #include<iostream>
 using namespace std;
 const int maxn = ;//位数
 int f[maxn];//上限1000!有2000+位，1005*6位足够了

 int main()
 {
     int n;
     while (cin>>n)
     {
         memset(f, , sizeof(f));
         int len = ;//初始只有1位
         f[] = ;//1!=1
         for (int i = ; i <= n; i++)//从2开始到n求阶乘
         {
             int c = ;//表示进位
             for (int j = ; j < len; j++) //模拟乘法，用每位来乘以i
             {
                 int t = f[j] * i + c;
                 f[j] = t % ;
                 c = t / ;
             }
             if (c) f[len++] = c;//如果进位大于0，就新增一位
         }
         cout << n << "!" << endl;
         cout << f[len - ];
         for (int i = len - ; i >= ; i--)
             printf("%06d", f[i]);//“%06d"的0表示若f[i]不足6位前面补0
         cout << endl;
     }
 }