Huffman树与Huffman编码

• 1.Huffman树

今天复习Huffman树。依稀记得自己被Huffman树虐的经历。还记得是7月份，我刚开始看数据结构与算法，根本看不懂Huffman树的操作。后来我终于悟出了Huffman树是怎么操作的了，但是被C艹的指针虐：用C艹的CArray存贮结点，但是读出来是空的。这是因为当时使用了“CBTtree node;”这样的声明方式，因为C艹的变量的生命周期，一个语句块或者一个循环结束后node就被释放了。所以改为“ CBTtree * node = new CBTtree; ”就没有问题了。

后面又出现了一个逻辑盲区，就是在对CArray进行删除结点操作的时候，没有 “ if(pos[0]<pos[1]) pos[1]--; ”语句，导致删除了错误的结点或者越界错误。

Java code：

     void Huffman(int []nums){
         int len=nums.length;
         int i;
         List<BTNode> nodes=new ArrayList<BTNode>();
         for(i=0;i<len;i++){
             BTNode node=new BTNode(nums[i]);
             nodes.add(node);
         }
         while(nodes.size()>1){
             int pos[]={0,0};
             int min[]={0x7FFFFFFF,0x7FFFFFFF};    //index=0: 最小 ， index=1: 次小
             for(i=0;i<nodes.size();i++){
                 int value=Integer.parseInt(nodes.get(i).data);
                 if(value<min[0]){
                     min[1]=min[0];//传递，最小值被占据，理应把原来的最小值传给次小值
                     pos[1]=pos[0];
                     min[0]=value;
                     pos[0]=i;
                 }else if(value<min[1]){//通过 else if 语句，说明次小值是大于最小值，但是小于原次小值的
                     min[1]=value;
                     pos[1]=i;
                 }
             }
             //将两个最小的节点取出，用他们的之的和形成一个新的节点
             BTNode parent=new BTNode();
             parent.data=String.valueOf(min[0]+min[1]);
             parent.lChild=nodes.get(pos[0]);
             parent.rChild=nodes.get(pos[1]);
             //将两个节点取出
             nodes.remove(pos[0]);
             if(pos[0]<pos[1]) pos[1]--;//☆☆如果出现这个逻辑盲点，将导致代码出错
             nodes.remove(pos[1]);
             nodes.add(parent);
         }
         root=nodes.get(0);
     }

输入：5,3,7,8,11,14,23,29

输出：

---

• 2.Huffman编码

前缀编码：任一个编码都不是另一个字符编码的前缀

     void HuffmanCode(BTNode parent,String code){
         if(parent.lChild==null) {System.out.println(parent.data+" : "+code);return;}
         else HuffmanCode(parent.lChild,code+"0");
         if(parent.rChild==null) {System.out.println(parent.data+" : "+code);return;}
         else HuffmanCode(parent.rChild,code+"1");
     }

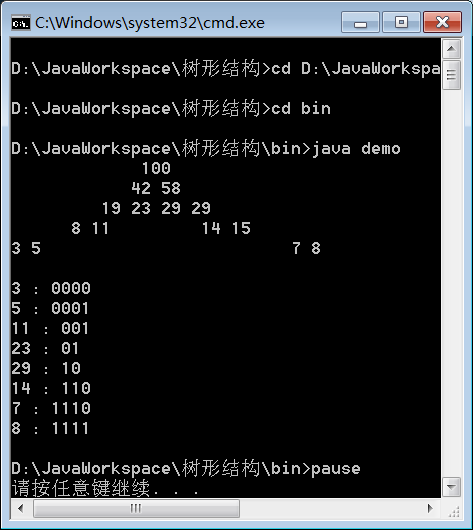
输入：

5,3,7,8,11,14,23,29

输出：