Codeforces Round #557 题解

掉分快乐

CF1161A Hide and Seek

Alice和Bob在玩捉♂迷♂藏，有$n$个格子，Bob会检查$k$次，第$i$次检查第$x_i$个格子，如果Alice在这个格子就输了。Alice一开始会在一个格子，可以在Bob检查过一次后向一个相邻的格子移动（整局游戏只能用一次）。求Alice有多少种方案赢。

两个方案相同当且仅当Bob检查之前Alice的位置和Bob做完所有检查之后Alice的位置都相同。

cao，sb阅读题。。。

直接枚举方案判断即可

https://codeforces.com/contest/1161/submission/53750223

CF1161B Chladni Figure

有一个圆形光碟，圆上均匀放着$n$个点。一些点之间有连边。

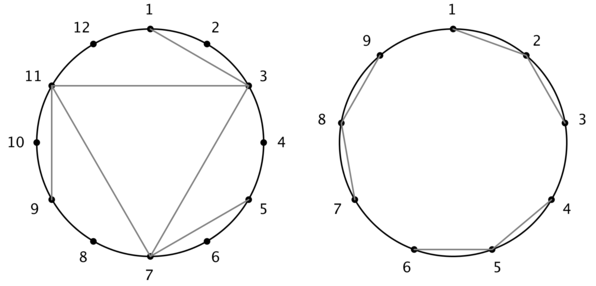
问这个光碟是否可以旋转一定角度和自己相等。（显然不能是360度）

kao我是sb这都不会了。。。

对一个角度暴力判断是$O(n)$的，然后可能的角度肯定是$n$的约数就做完了。。

https://codeforces.com/contest/1161/submission/53768643

CF1161C Thanos Nim

取石子游戏，每次选择$n/2$堆取任意数量石子，不能操作者输。

（此题我还是不知道是啥意思，"They can remove a different number of stones from the piles in a single turn"这句话太鬼了）

显然的可以知道，如果有人取完一堆石头这个人就输了。

如果最小值的数量小于等于$n/2$则Alice赢，否则Bob赢。

如果现在在必胜态，就有$\geq n/2$个石子严格大于当前最小值，将它们减到最小值，就到达了必败态。

如果是必败态，至少会取到一个最小值的堆减小最小值，那么新的最小值数量最多也就$n/2$个。

https://codeforces.com/contest/1161/submission/53769976

CF1161D Palindrome XOR

有一个数字串$s$，由0、1和?组成，串长为$n$，第0位是1。你要取两个数$a,b$，满足以下条件：

$0<a<b<2^n$
$a$和$b$去掉前导$0$之后是回文数字
$a\text{ xor }b$的二进制表示与给定的数字串匹配。?可以匹配0和1，0和1只能匹配对应的数字。

由只有0和1可以想到图的染色。

因为$s$保证了第0位是1，那么显然$a$第0位是0，$b$第0位是1，b的长度就一定是$n$了。枚举$a$的长度$l$，建一张图。对$a,b$每一位都建一个点，设为$A_i,B_i$，再建一个$I$点表示$0$。

点的颜色只有$0,1$两种，边有权值$0$或$1$，意义是连的两个点颜色相等/不等。

显然连边满足条件。第一个条件已经满足了，再看第二个条件，对于$a$只需要对所有满足条件的$i,j$连边$(A_i,A_j,0)$即可，$b$一样。

第三个条件也很好满足，将对应位置的$A_i,B_i$连边$(A_i,B_i,s_i)$即可。如果$s_i$是?不需要连边，如果$A_i$不存在就是$0$，向$I$连边。

还有，因为第一位一定是是$1$，所以连边$(B_1,I,1),(A_{n-lena+1},I,1)$。

对整个图进行染色，如果可以染色，设联通块数量是$C$，答案加上$2^{C-1}$，因为$I$一定取$0$，剩下的联通块可以任意交换$0,1$。

https://codeforces.com/contest/1147/submission/53788363

CF1161E Rainbow Coins

交互题

有$n$个硬币，每个硬币有3种可能颜色。

你可以拿出两个硬币询问颜色是否相等。

你每次可以同时询问若干对硬币，但是一次询问中不能有硬币被询问过2次。

最后输出三组数，每一组里的硬币颜色应该相同。

最多询问7次。（一次可以同时询问多组）

首先询问两次，第一次询问$(2i-1,2i)(i\geq 1)$，第二次询问$(2i,2i+1),\cdots(i\geq 1)$，相邻的两个如果相同就缩起来，这样序列相邻两个都不同了。

然后在缩完以后的序列上询问两次，都询问$(i,i+2)(i\geq 1)$，两次可以问完。通过这个可以求出$last_i$表示$i$与$i-2$颜色是否相等。

然后就可以递推一遍求出答案了。前两块颜色分别是0,1，然后递推到块$i$时，如果$lst_i=1$，那么$col_i=col_{i-2}$，否则因为$col_i\neq col_{i-1},col_i\neq col_{i-2}$，$i$的颜色还是唯一确定的。

https://codeforces.com/contest/1161/submission/53793188

CF1161F Zigzag Game

有一个二分图，左右各$n$个点，边有权值。alice和bob在上面玩游戏，alice先选择“增加”或者“减少”，bob会选择剩下的，然后alice选一个开始点，双方轮流在二分图上移动，bob先任意移动一步，然后如果alice选了增加，alice移动的边较上次必须严格更大，bob同理。显然无法移动就输了。而且不能走到以前走到过的点。你要和judger玩这个游戏，你先选则玩alice还是bob，然后玩游戏，显然你要赢。

因为zsy太强了，bob是实际意义上的先手，当然选bob了。（而且样例2说明了选alice可能直接暴毙）

还是因为zsy太强了，在二分图上的博弈要先找一个匹配，每次直接走匹配上的边。

假设Alice选了“增加”（否则取反所有边权）并选一个左边的点开始。如果有连续的三步$a\rightarrow b\rightarrow c\rightarrow d$，且$a,c$在左边，$b,d$在右边，那么$a\rightarrow b,c\rightarrow d$是bob走的，$b\rightarrow c$是alice走的。因为移动的“增加”“减少”限制，我们需要满足$W_{a,b}<W_{b,c},W_{b,c}>W_{c,d}$。

还是因为zsy太强了，这是一个稳定婚姻问题，左边点对于右边点的权值是边权，右边对于左边点的是边权相反数。

https://codeforces.com/contest/1161/submission/53810373