OpenFOAM——圆筒壁稳态导热

对于圆筒壁的稳态导热，温度分布的解析解为：

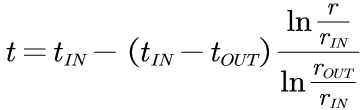
IN为恒温边界，设置为300K，OUT也为恒温边界，设置为500K

固体导热系数为：0.0887W/(m·K)

首先进行建模操作，任何建模软件均可，本算例采用ICEM直接建模，生成网格，缩放网格，然后利用OpenFOAM下转化网格，划分完成的网格如下：

接下来转入OpenFOAM的操作：

首先新建一个文件夹，名字任取，用来作为算例文件夹，本算例中我将该文件夹命名为：solid

然后进入OpenFOAM的安装目录，将安装目录下的flange算例（我的目录为/opt/openfoam5/tutorials/basic/laplacianFoam/flange）下的0文件夹、constant文件夹和system文件夹拷贝到solid文件夹下，然后删除system目录下的blockMeshDict文件，因为我们利用OpenFOAM的命令转化.msh文件为OpenFOAM能接受的网格文件。

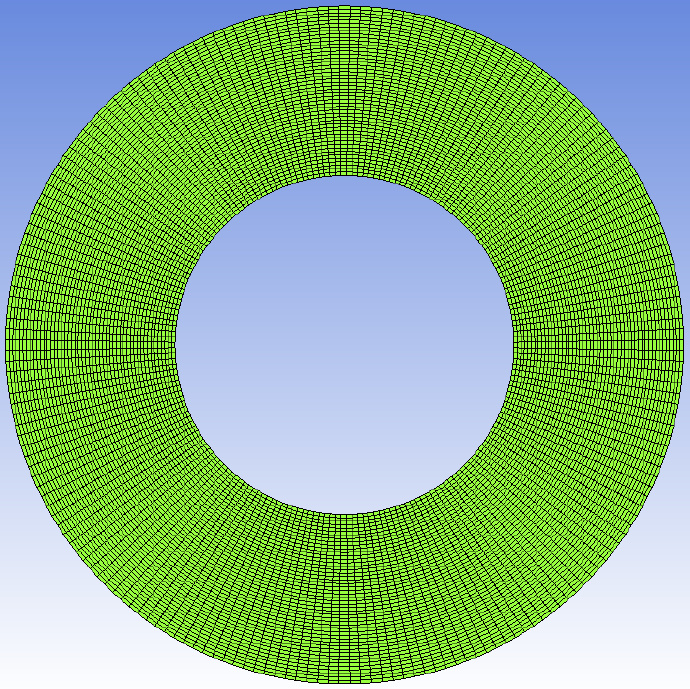
然后我们将刚才我们生成的.msh网格拷贝到solid文件夹下。在算例文件夹下打开终端，输入fluentMeshToFoam命令：

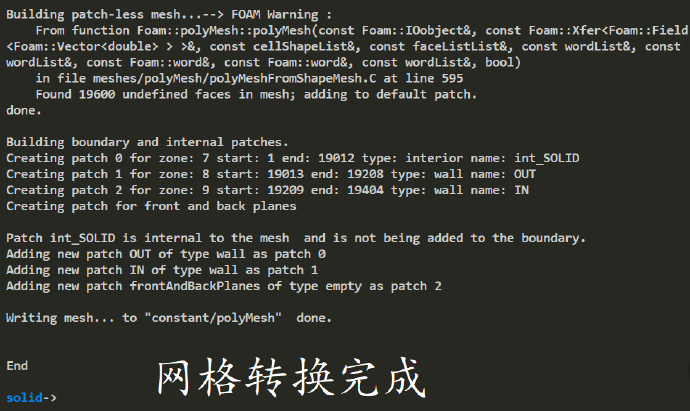
我们打开constant文件夹下的transportproperties文件，内容修改如下：

然后对初始边界条件进行设置，下面转入0文件夹下进行操作：

T文件当中的内容如下：

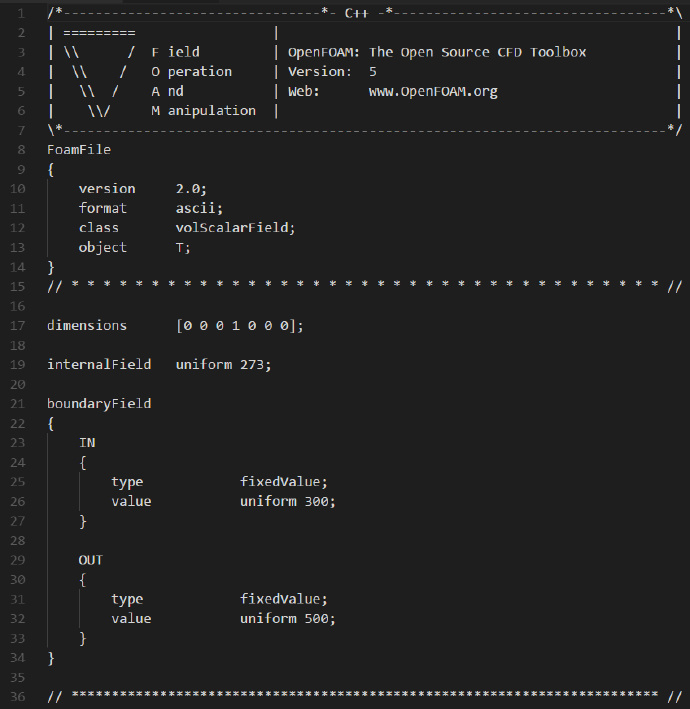
其他保持默认即可

在终端中输入laplacianFoam开始计算：

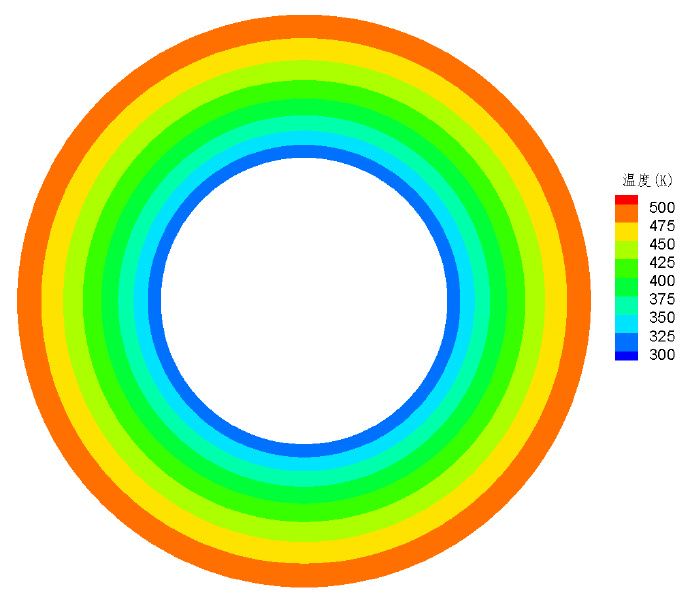
等到计算结束

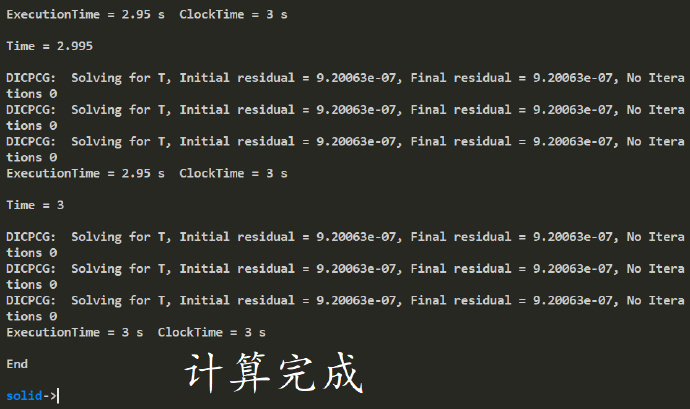
温度云图

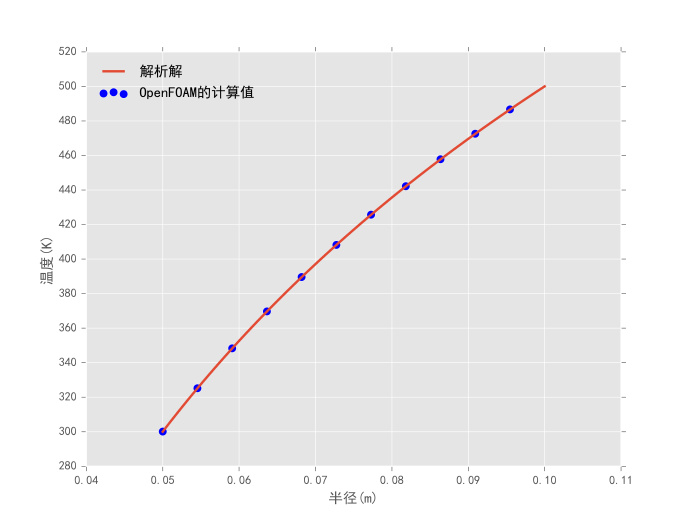
计算结果与解析解的对比