数学：拓展BSGS

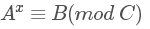
当C不是素数的时候，之前介绍的BSGS就行不通了，需要用到拓展BSGS算法

方法转自https://blog.csdn.net/zzkksunboy/article/details/73162229

典型例题是POJ3243

 #include<cstdio>
 #include<cmath>
 #include<algorithm>
 using namespace std;
 struct Hashmap
 {
     static const int Ha=,maxe=;
     int E,lnk[Ha],son[maxe+],nxt[maxe+],w[maxe+];
     int top,stk[maxe+];
     void clear() {E=;while (top) lnk[stk[top--]]=;}
     void Add(int x,int y) {son[++E]=y;nxt[E]=lnk[x];w[E]=0X7fffffff;lnk[x]=E;}
     bool count(int y)
     {
         int x=y%Ha;
         for (int j=lnk[x];j;j=nxt[j])
             if (y==son[j]) return true;
         return false;
     }
     int& operator [] (int y)
     {
         int x=y%Ha;
         for (int j=lnk[x];j;j=nxt[j])
             if (y==son[j]) return w[j];
         Add(x,y);stk[++top]=x;return w[E];
     }
 }f;
 int gcd(int a,int b)
 {
     return b==?a:gcd(b,a%b);
 }
 int exgcd(int a,int b,int &x,int &y)
 {
     if(b==) {x=;y=;return a;}
     int r=exgcd(b,a%b,x,y);
     int t=x;x=y;y=t-a/b*y;
     return r;
 }
 int exBSGS(int A,int B,int C)
 {
     if(C==) if(B==) return A!=; else return -;
     if(B==) if(A!=) return ; else return -;
     if(A%C==) if(B==) return ; else return -;
     int r,D=,num=;
     while((r=gcd(A,C))>)
     {
         if(B%r) return -;
         num++;
         B/=r;C/=r;D=((long long)D*A/r)%C;
     }
     for(int i=,tmp=;i<num;i++,tmp=((long long)tmp*A)%C)
         if(tmp==B) return i;
     int m=ceil(sqrt(C)),Base=;f.clear();
     for(int i=;i<=m-;i++)
     {
         f[Base]=min(f[Base],i);
         Base=((long long)Base*A)%C;
     }
     for(int i=;i<=m-;i++)
     {
         int x,y,r=exgcd(D,C,x,y);
         x=((long long)x*B%C+C)%C;
         if(f.count(x)) return i*m+f[x]+num;
         D=((long long)D*Base)%C;
     }
     return -;
 }
 int main()
 {
     int A,B,C;
     while(scanf("%d%d%d",&A,&C,&B)==)
     {
         if(!A&&!B&&!C) break;
         int ans=exBSGS(A,B,C);
         if(ans==-) printf("No Solution\n");
         else printf("%d\n",ans);
     }
     return ;
 }

给哈希好评，哪天好好整理一下