P1886 滑动窗口

题目描述

现在有一堆数字共N个数字（N<=10^6），以及一个大小为k的窗口。现在这个从左边开始向右滑动，每次滑动一个单位，求出每次滑动后窗口中的最大值和最小值。

例如：

The array is [1 3 -1 -3 5 3 6 7], and k = 3.

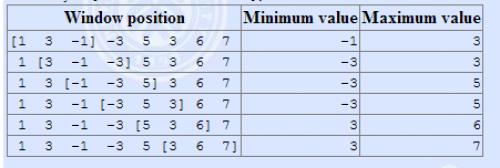
输入输出格式

输入格式：

输入一共有两行，第一行为n,k。

第二行为n个数(<INT_MAX).

输出格式：

输出共两行，第一行为每次窗口滑动的最小值

第二行为每次窗口滑动的最大值

输入输出样例

输入样例#1：

8 3
1 3 -1 -3 5 3 6 7

输出样例#1：

-1 -3 -3 -3 3 3
3 3 5 5 6 7

说明

50%的数据，n<=10^5

100%的数据，n<=10^6

Solution：

　　本题是单调队列的模板题。。。

　　单调队列思想虽简单，但是代码各种判断很容易出错，于是打了一个线段树水一波分。

　　思路就是区间查询最值，维护一下就$OK$了。

代码：

#include<bits/stdc++.h>
#define il inline
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
const int inf=,N=1e6+;
using namespace std;
int n,k,cnt,ans1[N],ans2[N];
struct node{
    int maxn,minn;
}tr[N<<];
il int gi(){
    int a=;char x=getchar();bool f=;
    while((x<''||x>'')&&x!='-')x=getchar();
    if(x=='-')x=getchar(),f=;
    while(x>=''&&x<='')a=a*+x-,x=getchar();
    return f?-a:a;
}
il int Max(int a,int b){return a>b?a:b;}
il int Min(int a,int b){return a>b?b:a;}
il void pushup(int rt){
    tr[rt].maxn=Max(tr[rt<<].maxn,tr[rt<<|].maxn);
    tr[rt].minn=Min(tr[rt<<].minn,tr[rt<<|].minn);
}
il void build(int l,int r,int rt){
    if(l==r){tr[rt].maxn=tr[rt].minn=gi();return;}
    int m=l+r>>;
    build(lson),build(rson);
    pushup(rt);
}
il void query(int L,int R,int l,int r,int rt,int cnt){
    if(L<=l&&R>=r){ans1[cnt]=Min(ans1[cnt],tr[rt].minn);ans2[cnt]=Max(ans2[cnt],tr[rt].maxn);return;}
    int m=l+r>>;
    if(L<=m)query(L,R,lson,cnt);
    if(R>m)query(L,R,rson,cnt);
}
int main(){
    n=gi(),k=gi()-;
    for(int i=;i<=n;i++)ans1[i]=inf,ans2[i]=-inf;
    build(,n,);
    for(int i=;i+k<=n;i++)query(i,i+k,,n,,++cnt);
    for(int i=;i<=cnt;i++)printf("%d ",ans1[i]);
    printf("\n");
    for(int i=;i<=cnt;i++)printf("%d ",ans2[i]);
    return ;
}