K：二叉树

相关介绍:

 二叉树是一种特殊的树，它的每个节点最多只有两棵子树，并且这两棵子树也是二叉树。由于二叉树中的两棵子树有左右之分，为此，二叉树是有序树。

二叉树的定义：

 二叉树是由n(n>=0)个节点所以构成的有限集合。当n=0时，这个集合为空，此时的二叉树为空树；当n>0时，这个集合是由一个根节点和两个互不相交的分别称为左子树和右子树的二叉树所构成。

二叉树的存储结构:

 二叉树的存储实现有多种方式，但是归纳起来主要分为顺序存储和链式存储两大类。下面用于介绍这两种存储方式:

顺序存储:

 二叉树的顺序存储是指按照某种顺序依次将二叉树中的各个节点的值存放在一组地址连续的存储单元中。由于二叉树是非线性结构，所以需要将二叉树中的各个节点先按照一定的顺序排列成一个线性序列，再通过这些节点在线性序列中的相对位置，确定二叉树的各个节点之间的逻辑关系。对于一棵完全二叉树，我们可以从根节点开始自上而下并按照层次由左向右对节点依次进行编号，然后按照编号顺序依次将其存放在一维数组中。对于一棵非完全二叉树来说，可以先在此树中增加一些并不存在的虚节点并使其成为一棵完全二叉树，然后用与完全二叉树相同的方法对节点进行编号，再将编号为i的节点的值存放到数组下标为i的数组单元中，虚节点不存放任何值。如下图1.1所示

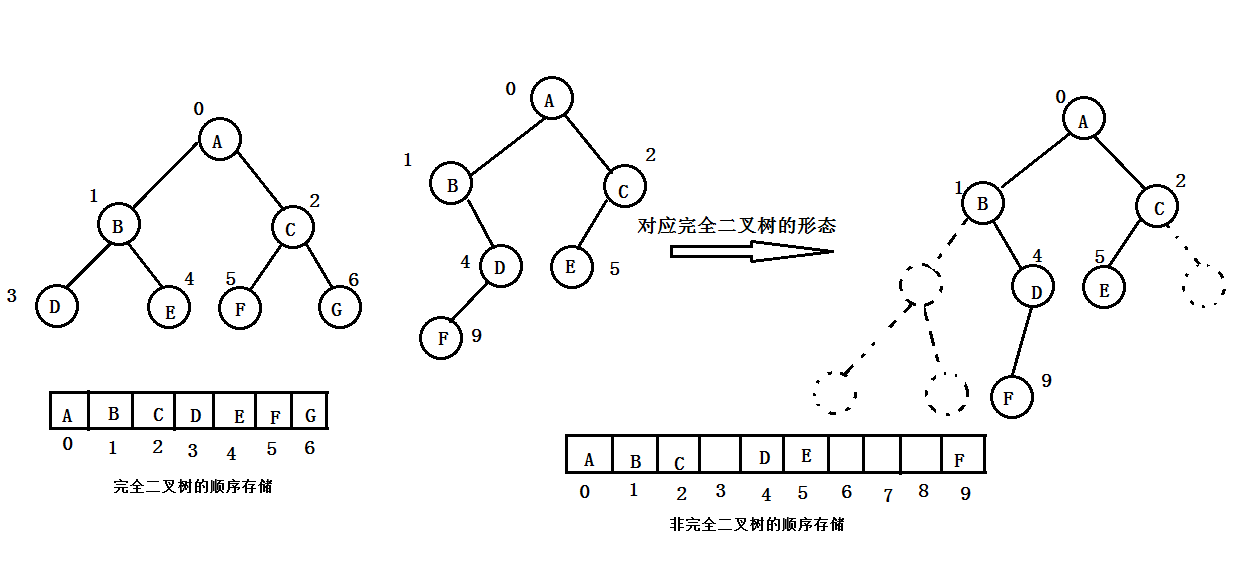
注意点:对于满二叉树和完全二叉树来说，顺序存储是一种最简单，最节省空间的存储方式，而且其操作简单，所以顺序存储方式非常适用于满二叉树和完全二叉树。但对于非完全二叉树，由于“虚节点”的存在从而造成了存储空间的浪费。

链式存储：

 二叉树的链式存储是指将二叉树的各个节点随机的存放在位置任意的内存空间中，各个节点之间的逻辑关系通过指针来反映，由于二叉树中的任意一个节点至多只有一个双亲节点和两个孩子节点，所以在用链式存储方式来实现二叉树的存储时，可以有两种方式，一种是二叉链表存储结构；一种是三叉链表存储结构。在二叉链表结构中，二叉树中的每个节点设置有三个域，一个数据域，左孩子域和右孩子域。其中，数据域用来存放节点的值。左右孩子域分别用来存放该节点的左、右孩子节点的存储地址。三叉链表结构是指在二叉链表结构的基础上增加了一个父节点域，该域用来存放此节点的父节点的存储地址。三叉链式存储结构既便于查找孩子节点，又便于查找双亲节点，当它相对二叉链表存储结构来说，增加了存储空间的开销。因此，在实际应用中，二叉链表结构是二叉树最为常用的存储结构。图1.2和图1.3演示了三叉链表存储结构和二叉链表存储结构

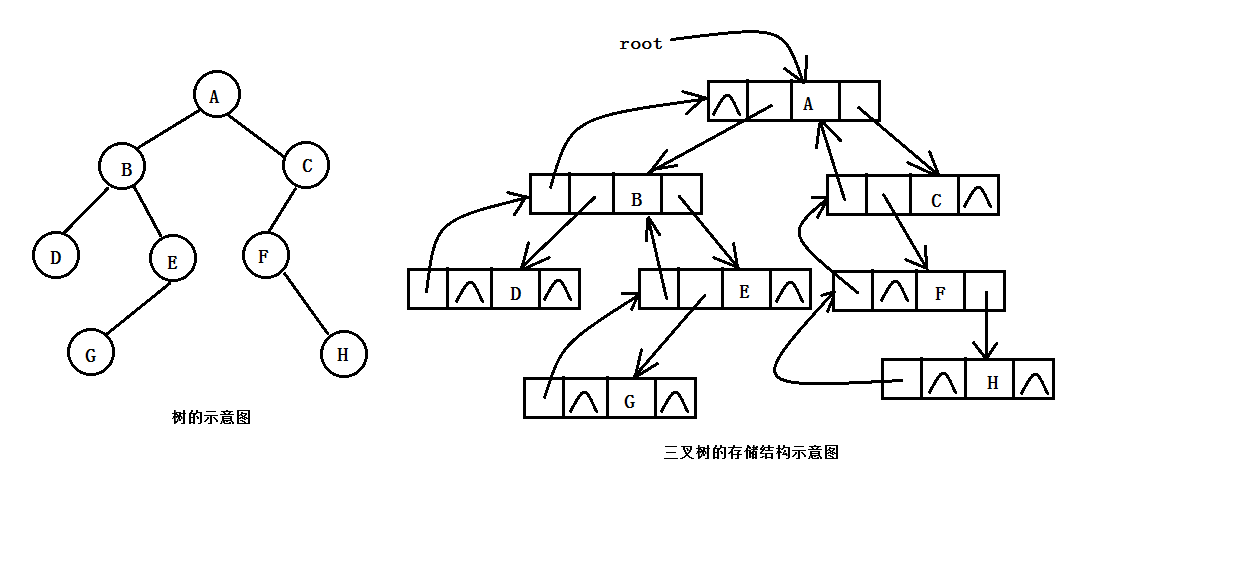
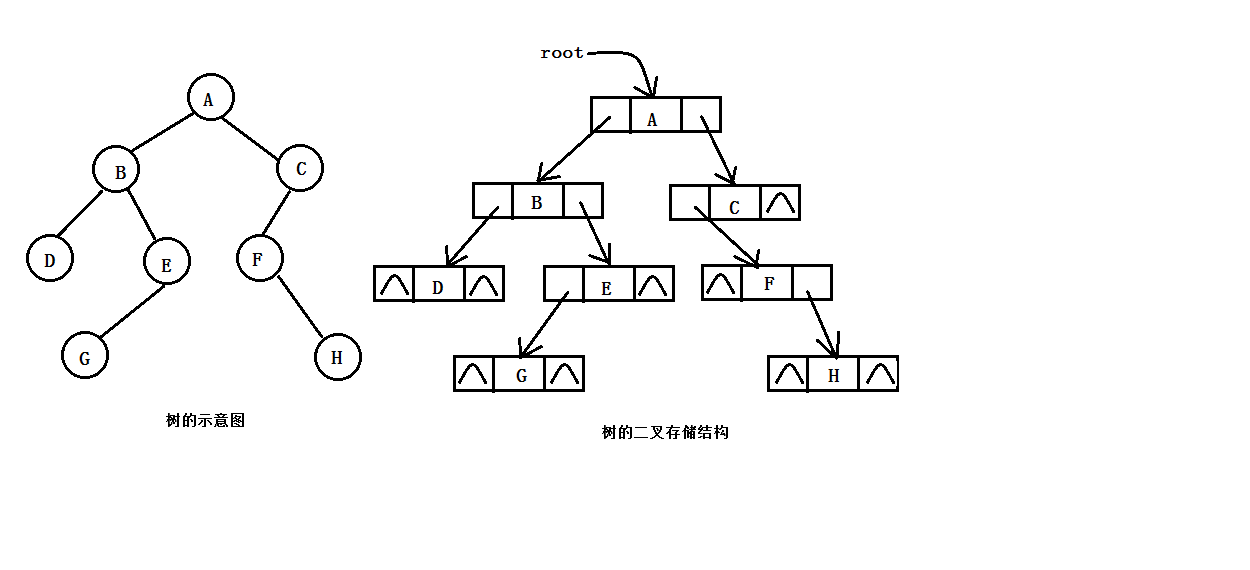
需要注意的是：二叉树的存储结构中，有分带头节点和不带头节点的这两种情况，带头节点的二叉树，其头节点不存储任何数据，而不带头节点的二叉树，其第一个节点便存储相关的数据。为方便起见，以下的代码演示的均是不带头节点的情况

相关代码:

三叉链表存储结构的节点描述：

class Node
{
    //用于记录双亲节点的指针
    Node parent;
	//用于记录左孩子的指针
	Node left;
	//用于记录右孩子的指针
	Node right;
	//用于记录节点数据的对象指针
	T data;
}

二叉链表存储结构的节点描述：

class Node
{
	//用于记录左孩子的指针
	Node left;
	//用于记录右孩子的指针
	Node right;
	//用于记录节点数据的对象指针
	T data;
}

二叉链表存储结构下的二叉树类的描述：

package all_in_tree;
/**
 * 该类用于演示二叉树的情况
 * @author 学徒
 *
 */
public class BinaryTree
{
	class Node
	{
		//用于记录左孩子的指针
		Node left;
		//用于记录右孩子的指针
		Node right;
		//用于记录节点数据的对象指针
		Object data;

		public Node(Object data)
		{
			this(data,null,null);
		}
		public Node(Object data,Node left,Node right)
		{
			this.data=data;
			this.left=left;
			this.right=right;
		}
	}
	//根节点的对象
	private Node root;
	//用于创建一棵空树
	public BinaryTree()
	{
		root=null;
	}
	//用于创建一棵一某个节点为根节点的树
	public BinaryTree(Node root)
	{
		this.root=root;
	}
	/**
	 * 根据先根遍历和中根遍历的序列创建一棵二叉树
	 * @param preOrder 先序遍历的序列
	 * @param inOrder 中序遍历的序列
	 * @param preIndex 先序遍历中根节点所在的序列
	 * @param inIndex 中序遍历中根节点所在的序列
	 * @param count 子树序列的长度
	 * 其步骤如下:
	 * 1. 先判断先/中序遍历序列是否为空
	 * 2. 找到其对应的根节点
	 * 3. 找根节点在中序遍历序列中的位置
	 * 4. 建立根节点
	 * 5. 建立左右子树
	 */
	public BinaryTree(String preOrder,String inOrder,int preIndex,int inIndex,int count)
	{
		if(count>0)
		{
			char r=preOrder.charAt(preIndex);
			int i=0;
			for(;i<count;i++)
			{
				if(r==inOrder.charAt(inIndex+i))
					break;
			}
			root =new Node(r);
			root.left=(new BinaryTree(preOrder,inOrder,preIndex+1,inIndex+1,i)).root;
			root.right=(new BinaryTree(preOrder,inOrder,preIndex+i+1,inIndex+i+1,count-i-1)).root;
		}
	}
}

二叉树的基本操作：

 对于二叉树，其遍历操作为其基本的操作。遍历的方式有四种，分别为层次遍历、先序遍历、中序遍历、后序遍历，下面将分别介绍这四种遍历方式

层次遍历:

 对于层次遍历，其按照的是的各个节点在树中所处的层次顺序进行遍历的。其操作步骤为,先访问第0层的根节点，然后从左到右依次访问第1层的每一个节点，依次类推，当第i层上的所有节点都访问完后，再从左往右依次访问第i+1层的每一个节点，知道最后一层的所有节点都访问完为止。为此，为实现二叉树的层次遍历，应当使用一个队列依次沿着树的访问记录下其相关节点的孩子节点。其相关代码如下:

相关代码:

private static Queue<Node> q=new LinkedList<Node>();
public static void greed(Node root)
{
	if(root!=null)
		q.add(root);
	while(!q.isEmpty())
	{
		Node node=q.poll();
		//遍历其相关的节点的数据
		System.out.print(node.data+"  ");
		if(node.left!=null)
			q.add(node.left);
		if(node.right!=null)
			q.add(node.right);
	}
}

先序遍历:

 所谓的先序遍历，是指先访问其根节点后递归的依次访问其左子树和右子树的方式，其递归遍历方式的相关代码如下:

相关代码:

public void preRoot(Node root)
{
    if(root!=null)
    {
        System.out.print(root.data+" ");
        preRoot(root.left);
        preRoot(root.right);
    }
}

中序遍历:

 所谓的中序遍历，是指先访问其左子树，然后访问其根节点，之后再访问其右子树的一种遍历方式，其递归遍历方式的相关代码如下:

public void inRoot(Node root)
{
    if(root!=null)
    {
        inRoot(root.left);
        System.out.print(root.data+" ");
        inRoot(root.right);
    }
}

后序遍历:

 所谓的后序遍历，是指先访问其左子树，让后再访问其右子树，最后在访问其根节点的一种遍历方式，其递归遍历方式的相关代码如下:

public void postRoot(Node root)
{
    if(root!=null)
    {
        postRoot(root.left);
        postRoot(root.right);
        System.out.print(root.data+" ");
    }
}

对于以上四种遍历方式中，其先序、中序、后序遍历方式可以采用非递归的方式，其非递归遍历方式的实现，参看博文 K：二叉树的非递归遍历

回到目录|·(工)·）