2024-04-06：用go语言，给你两个非负整数数组 rowSum 和 colSum， 其中 rowSum[i] 是二维矩阵中第 i 行元素的和， colSum[j] 是第 j 列元素的和，换言之你

2024-04-06：用go语言，给你两个非负整数数组 rowSum 和 colSum，

其中 rowSum[i] 是二维矩阵中第 i 行元素的和，

colSum[j] 是第 j 列元素的和，换言之你不知道矩阵里的每个元素，

但是你知道每一行和每一列的和。

请找到大小为 rowSum.length x colSum.length 的任意 非负整数 矩阵。

且该矩阵满足 rowSum 和 colSum 的要求。

请你返回任意一个满足题目要求的二维矩阵，题目保证存在 至少一个 可行矩阵。

输入：rowSum = [3,8], colSum = [4,7]。

输出：[[3,0],[1,7]]。

答案2024-04-06：

来自左程云。

灵捷3.5

大体步骤如下：

1.初始化一个大小为rowSum.length x colSum.length的二维矩阵ans，用于存储最终的结果。

2.遍历rowSum数组，对于每个元素rowSum[i]，继续遍历colSum数组，对于每个元素colSum[j]：

• 将ans[i][j]设为rowSum[i]和colSum[j]中的较小值，即ans[i][j] = min(rowSum[i], colSum[j])。

• 更新rowSum[i]和colSum[j]，分别减去已经分配的值ans[i][j]，即rowSum[i] -= ans[i][j]，colSum[j] -= ans[i][j]。

3.返回ans作为结果矩阵。

总的时间复杂度：遍历rowSum和colSum数组需要$O(n^{2)$的时间复杂度，其中n是rowSum和colSum的长度。因此，总的时间复杂度为$O(n}2)$。

总的额外空间复杂度：额外使用了一个二维矩阵ans来存储结果，其大小为rowSum.length x colSum.length，因此总的额外空间复杂度为$O(n^2)$。

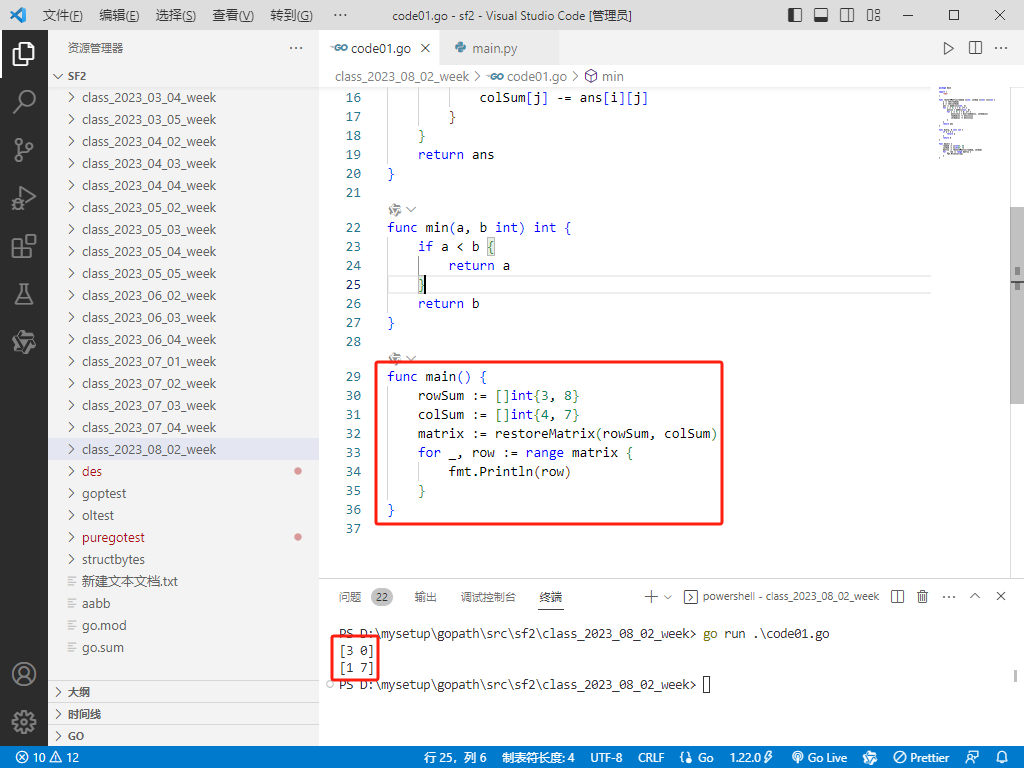
Go完整代码如下：

package main

import (
	"fmt"
)

func restoreMatrix(rowSum []int, colSum []int) [][]int {
	n := len(rowSum)
	m := len(colSum)
	ans := make([][]int, n)
	for i := 0; i < n; i++ {
		ans[i] = make([]int, m)
		for j := 0; j < m; j++ {
			ans[i][j] = min(rowSum[i], colSum[j])
			rowSum[i] -= ans[i][j]
			colSum[j] -= ans[i][j]
		}
	}
	return ans
}

func min(a, b int) int {
	if a < b {
		return a
	}
	return b
}

func main() {
	rowSum := []int{3, 8}
	colSum := []int{4, 7}
	matrix := restoreMatrix(rowSum, colSum)
	for _, row := range matrix {
		fmt.Println(row)
	}
}

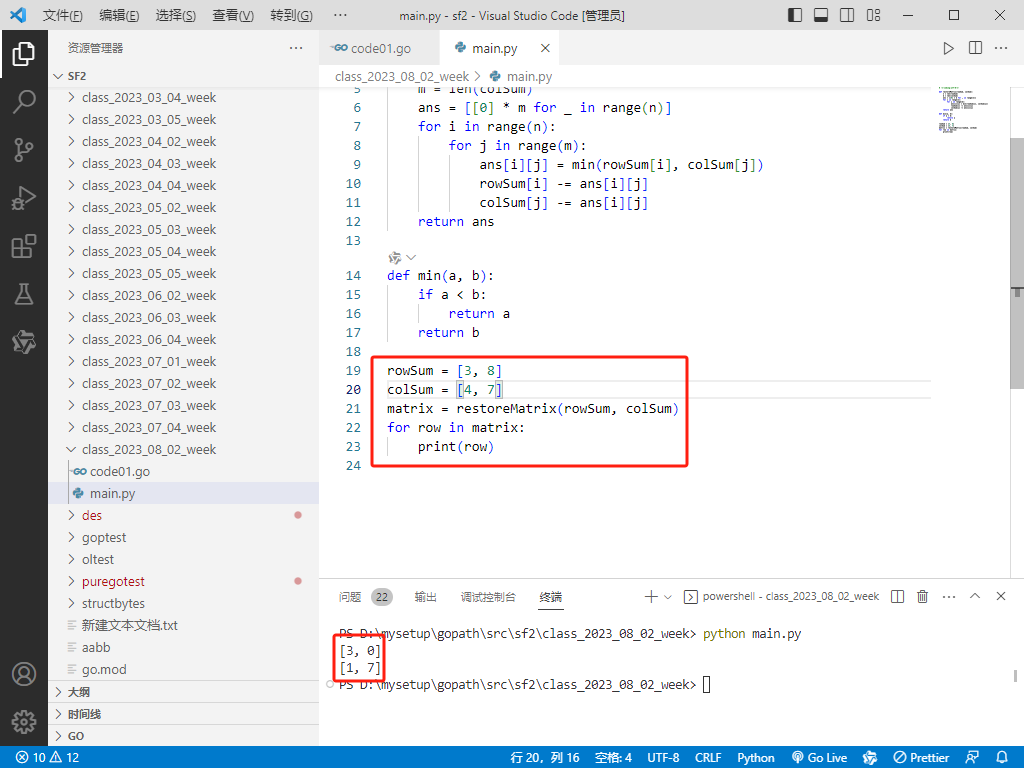
Python完整代码如下：

# -*-coding:utf-8-*-

def restoreMatrix(rowSum, colSum):
    n = len(rowSum)
    m = len(colSum)
    ans = [[0] * m for _ in range(n)]
    for i in range(n):
        for j in range(m):
            ans[i][j] = min(rowSum[i], colSum[j])
            rowSum[i] -= ans[i][j]
            colSum[j] -= ans[i][j]
    return ans

def min(a, b):
    if a < b:
        return a
    return b

rowSum = [3, 8]
colSum = [4, 7]
matrix = restoreMatrix(rowSum, colSum)
for row in matrix:
    print(row)