nlp入门（五）隐马尔科夫模型

源码请到：自然语言处理练习: 学习自然语言处理时候写的一些代码 (gitee.com)

一、马尔科夫模型概念

1.1 马尔科夫模型：具有马尔可夫性质并以随机过程为基础的模型

1.2 马尔科夫性质：过去状态只能影响现在状态，影响不了将来的状态

1.3 马尔科夫过程：随机过程满足马尔科夫性质，状态转移矩阵不会随着时间的变化而发生变化

1.4 马尔科夫模型举例

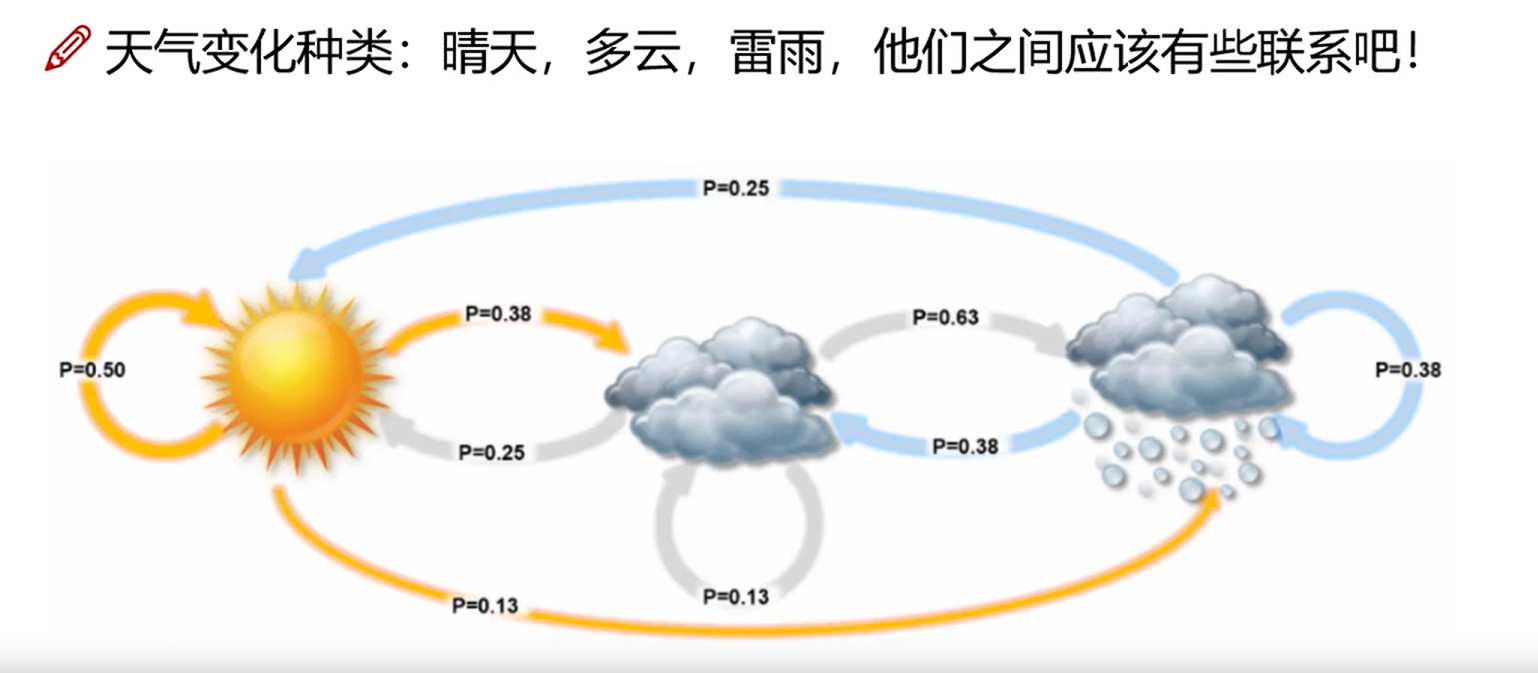
如图所示，天气有晴天、多云、雷雨三种状态，三种状态之间的变换是随机的，并且三种之间的状态概率是固定的，并且昨天的天气只能影响今天的天气，对明天的天气无法产生影响，就是一个马尔科夫模型。

二、隐马尔科夫模型

2.1 在马尔科夫模型中，无法直观的观察到状态，仅仅可以观测到表象，则称之为隐马尔科夫模型。

2.2 举例：在第一节的例子中，如果是在热带雨林中，看不见天所以无法直接观测到天气的情况，但是可以通过观察海藻的生长状态来判断当前的天气，这就是个隐马尔科夫模型

2.3 隐马尔科夫模型的表示

隐马尔科夫模型可以表示为：

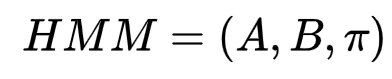
其中π为初始状态，A为状态转移概率矩阵，B为生成观测状态概率矩阵

2.4 隐马尔科夫模型要解决的问题

2.4.1 给定模型λ=（A,B,π）及观测序列O={o₁,o₂……o_T} 计算其出现的概率P(O|λ)

• 暴力求解法

推导过程如下：　

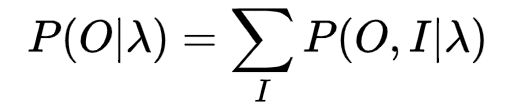
其中

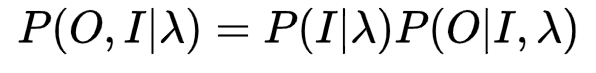
其中

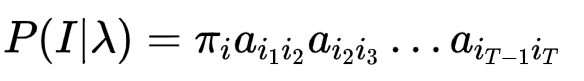
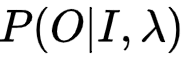就是B矩阵的内容

所以

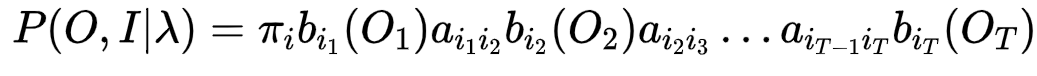
最终

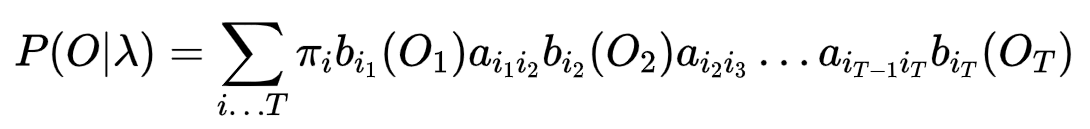
时间复杂度为O(TN^T) N为隐藏状态个数， 指数次复杂度，比较难得出结果

• 前向算法

在给定t时刻隐藏状态为i，观测序列为{O₁,O₂……O_T}的概率叫做前向概率

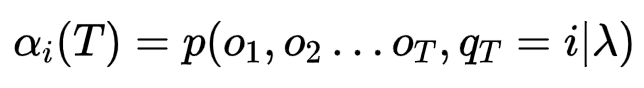
那么我们只需要求得T时刻所有隐藏状态的前向概率就可以了

又可以得到

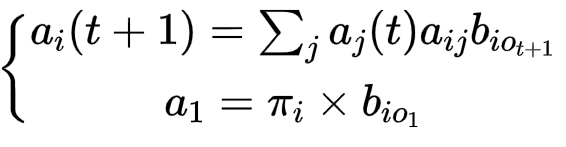
有了递推公式，则这个问题被转移成了一个动态规划，时间复杂度变为了O(N²T)

举例：

观测序列为{红 白 红}

在时刻1：

红色球，盒子1:

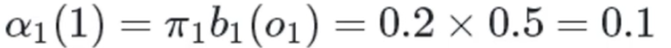
红色球，盒子2:

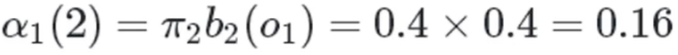
红色球，盒子3:

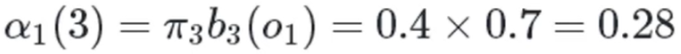
时刻2：

白色球，盒子1:

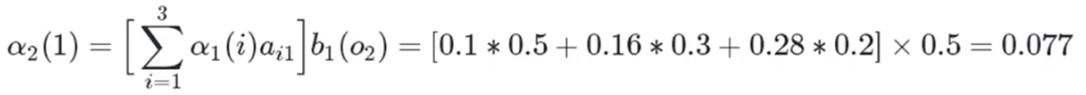
白色球，盒子2:

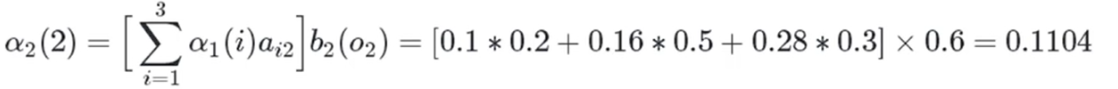
白色球，盒子3:

时刻3：

红色球，盒子1:

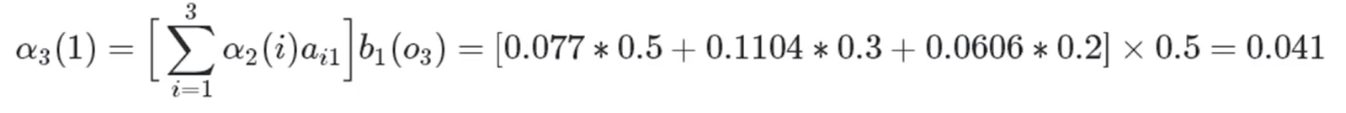
红色球，盒子2:

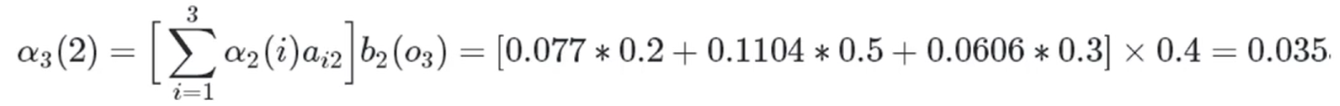
红色球，盒子3:

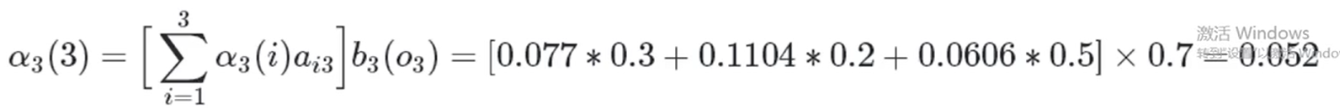
所以

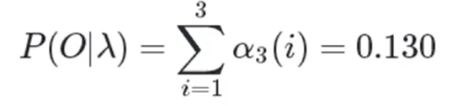
2.4.2 给定观测序列O={o₁,o₂……o_T} 求参数λ=（A,B,π）使得P(O|λ)最大

• 给定状态序列I={i₁,i₂……i_T}

给定状态序列的话，模型参数十分好求

初始概率π直接查询状态序列就可以了

状态转移概率公式：

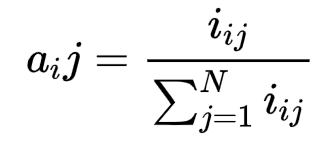
生成观测概率：

• 未给定状态序列

需要使用em算法

列概率最大值的对数似然方程

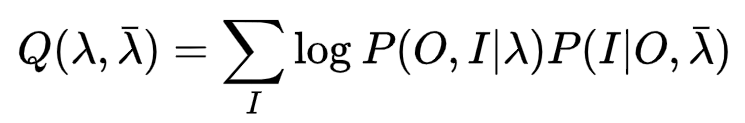
其中后部分

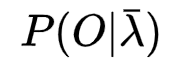可视为一个常数

所以

其中三部分分别仅存在π、A、B参数，分别使用拉格朗日乘子法就可以求解

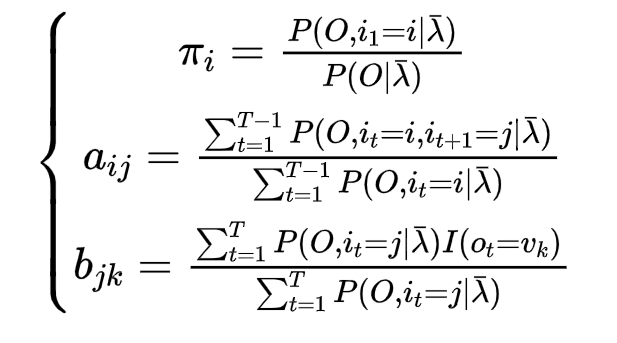
2.4.3 已知模型λ=（A,B,π）和观测序列O={o₁,o₂……o_T} ，求状态序列I={i₁,i₂……i_T}使得P(O|λ)最大

维特比算法

对于t时刻，隐藏状态为i，要找到所有可能路径的最大值

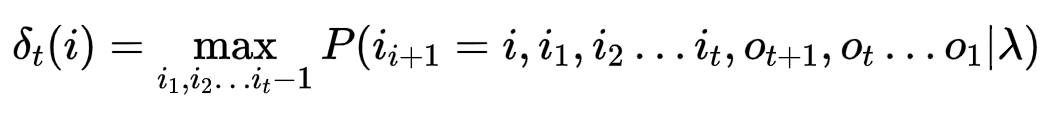
递推公式为

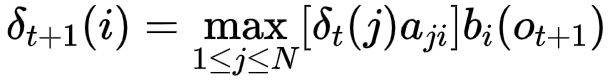
概率最大路径中t-1的状态为

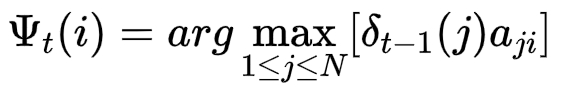
举例：

观测到序列为 {红 白 红}

t1时刻

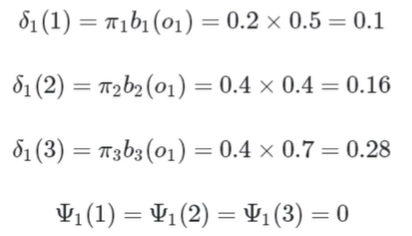
t2时刻

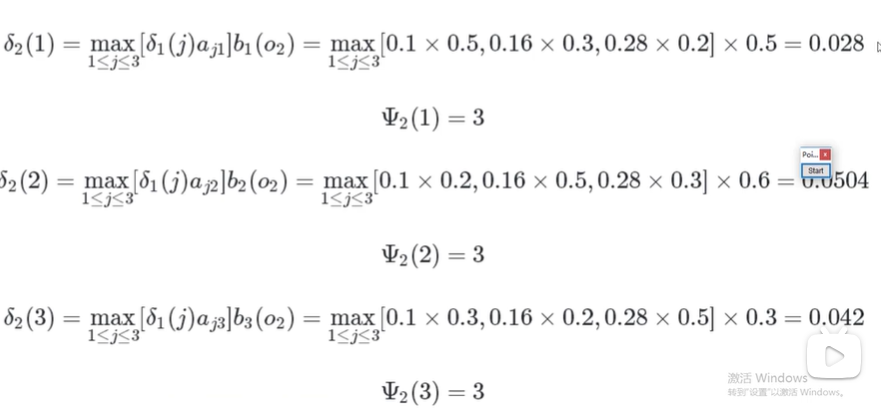
t3时刻

此时3最大，所以隐藏序列为（3,3,3）

三、hmmlearn工具安装

hmmlearn工具安装十分方便，执行

pip install hmmlearn

就可以了

四、维特比算法求隐藏序列

# 隐藏状态:三个盒子
states = ['box1', 'box2', 'box3']
n_states = len(states)

# 观测状态:两种球
observations = ['red', 'white']
n_observations = len(observations)

# 模型参数
start_probability = np.array([0.2, 0.4, 0.4])
transition_probability = np.array([
    [0.5, 0.2, 0.3],
    [0.3, 0.5, 0.2],
    [0.2, 0.3, 0.5]
])
emission_probability = np.array([
    [0.5, 0.5],
    [0.4, 0.6],
    [0.7, 0.3]
])

# 用于离散观测状态的模型
model = hmm.CategoricalHMM(n_components=n_states)
model.startprob_ = start_probability
model.transmat_ = transition_probability
model.emissionprob_ = emission_probability
model.n_features = n_observations

# 维特比算法，假设看到的是[红,白,红]
seen = np.array([[0, 1, 0]]).T
logprob, box = model.decode(seen, algorithm='viterbi')
print(np.array(states)[box])

box2 = model.predict(seen)
print(np.array(states)[box2])

五、求当前模型下的概率值（log形式）

# 求观测序列的可能性
print(model.score(seen))

六、给定观测序列求模型参数使得概率最大

# em算法求模型参数
model2 = hmm.CategoricalHMM(n_components=n_states, n_iter=20, tol=0.01)
X2 = np.array([[0, 1, 0, 1], [0, 0, 0, 1], [1, 0, 1, 1]])
model2.fit(X2)
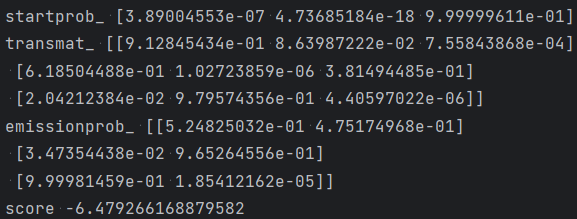
print('startprob_', model2.startprob_)
print('transmat_', model2.transmat_)
print('emissionprob_', model2.emissionprob_)
print('score', model2.score(X2))

七、基于HMM算法的中文分词

将字视为观测状态，将词的位置信息视为隐藏状态，就可以实现分词啦

# 实现中文分词
# {B（词开头），M（词中），E（词尾），S（独字词）}{0，1，2，3}
data = [{u'我要吃饭': 'SSBE'}, {u'天气不错': 'BEBE'}, {u'谢天谢地': 'BMME'}]

def getwords():
    res = []
    for line in data:
        for key in line:
            for word in key:
                if word not in res:
                    res.append(word)
    return ''.join(res)

def get_startprob(data):
    """
    获取bmes起始矩阵
    :return:起始矩阵
    """
    c = 0
    c_map = {'B': 0, 'M': 0, 'E': 0, 'S': 0}
    for v in data:
        for key in v:
            value = v[key]
        c = c + 1
        print('value[0] is ' + value[0])
        c_map[value[0]] = c_map[value[0]] + 1
        print('c_map[value[0]] is ' + str(c_map[value[0]]))
    res = []
    for i in 'BMES':
        res.append(c_map[i] / float(c))
    return res

def get_transmat(data):
    """
    获取状态转移矩阵
    :return:状态转移矩阵
    """
    c = 0
    c_map = {}
    for v in data:
        for key in v:
            value = v[key]
        print('value[0] is ' + value[0])
        for v_i in range(len(value) - 1):
            couple = value[v_i:v_i + 2]
            c_couple_source = c_map.get(couple, 0)
            c_map[couple] = c_couple_source + 1
            c = c + 1
    print('get_transmat\'s c_map is ' + str(c_map))
    res = []
    for i in 'BMES':
        col = []
        col_count = 0
        for j in 'BMES':
            col_count = c_map.get(i + j, 0) + col_count
        for j in 'BMES':
            col.append(c_map.get(i + j, 0) / float(col_count))
        res.append(col)
    return res

def get_emissionprob(data):
    """
    获取现象转换矩阵
    :return:现象转换矩阵
    """
    c_map = {}
    for v in data:
        for key in v:
            k = key
            value = v[key]
        print('value[0] is ' + value[0])
        for v_i in range(len(value)):
            couple = value[v_i] + k[v_i]
            print('emition\'s couple is ' + couple)
            c_couple_source = c_map.get(couple, 0)
            c_map[couple] = c_couple_source + 1
    res = []
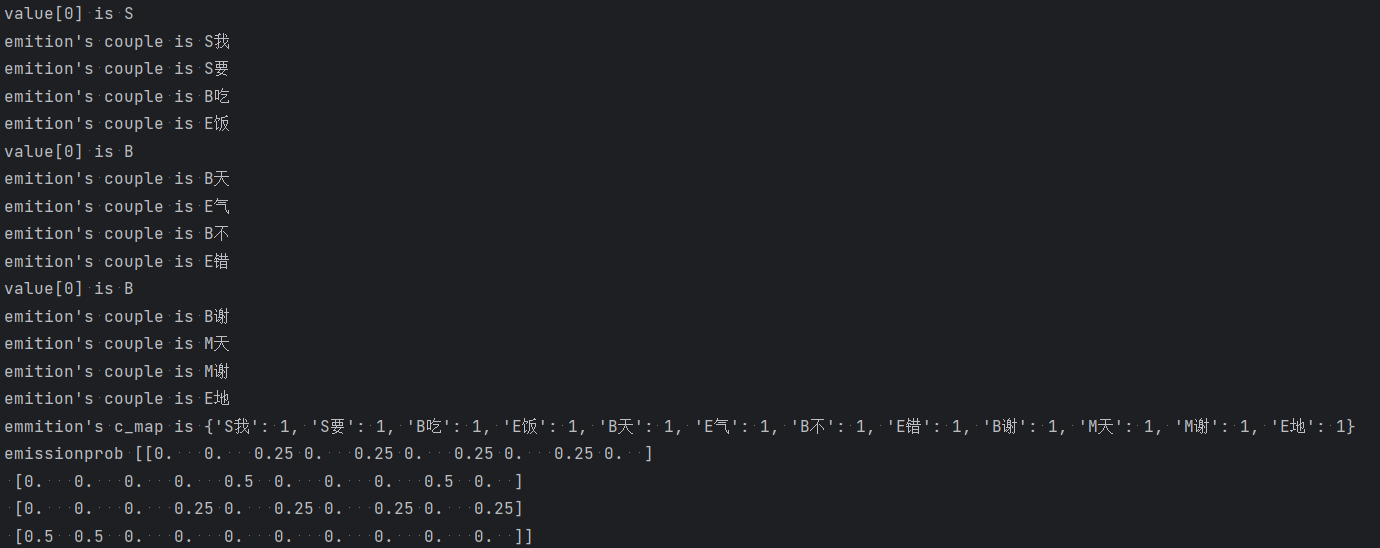
    print('emmition\'s c_map is ' + str(c_map))
    words = getwords()
    for i in 'BMES':
        col = []
        col_count = 0
        for j in words:
            col_count = c_map.get(i + j, 0) + col_count
        for j in words:
            col.append(c_map.get(i + j, 0) / float(col_count))
        res.append(col)
    return res

def get_array_from_phase(data, phase):
    c_map = {}
    c = 0
    for line in data:
        for key in line:
            for word in key:
                if word not in c_map.keys():
                    c_map[word] = c
                    c = c + 1
    res = []
    for word in phase:
        res.append(c_map[word])
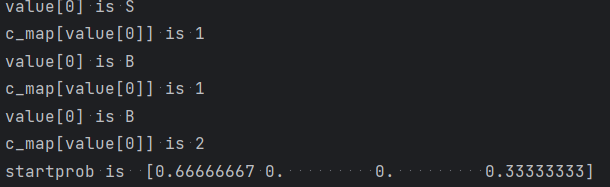
    return res

startprob = np.array(get_startprob(data))
print('startprob is ', startprob)
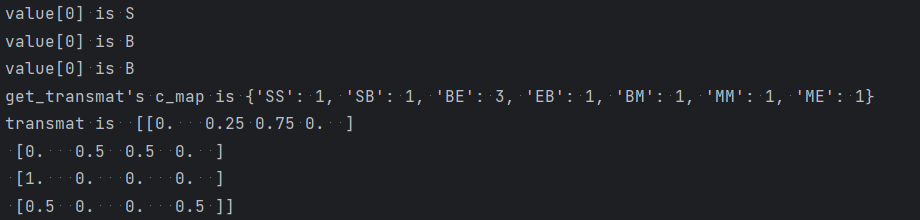
transmat = np.array(get_transmat(data))
print('transmat is ', transmat)
emissionprob = np.array((get_emissionprob(data)))
print('emissionprob', emissionprob)
cate_hmm = hmm.CategoricalHMM(n_components=4)
cate_hmm.startprob_ = startprob
cate_hmm.transmat_ = transmat
cate_hmm.emissionprob_ = emissionprob
phase = u'我要吃饭谢天谢地'
X = np.array(get_array_from_phase(data, phase))
X = X.reshape(len(phase), 1)
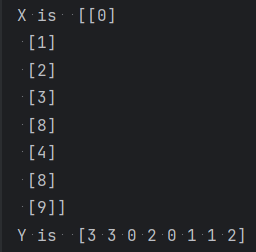
print('X is ', X)
Y = cate_hmm.predict(X)
print('Y is ', Y)