机器学习算法（一）：1. numpy从零实现线性回归

系列文章目录

机器学习算法（一）：1. numpy从零实现线性回归

机器学习算法（一）：2. 线性回归之多项式回归（特征选取）

@

目录

• 系列文章目录
• 前言
• 一、理论介绍
• 二、代码实现
  • 1、导入库
  • 2、准备数据集
  • 3、定义预测函数（predict）
  • 4 代价（损失）函数
  • 5 计算参数梯度
  • 6 批量梯度下降
  • 7 训练
  • 8 可视化一下损失
• 总结

---

前言

最近，想将本科学过的一些机器学习算法从零开始实现一下，毕竟天天当调包侠，虽然也能够很愉快的玩耍，但对于我这个强迫症患者是很难受的，底层逻辑是怎么样的，还是需要知道的。接下来我会从最简单的多元线性回归开始，一步一步在\(jupyter\)里面实现。

【注1】：本文默认读者具有基本的机器学习基础、\(numpy\)基础，如果没有建议看完吴恩达老师的机器学习课程在来看本文。

【注2】：本文大部分代码会采用向量化加速编程，当然部分情况下也会用到循环遍历的情况。后面有时间会再出一起循环遍历实现的。

【注3】：作者实力有限，有错在所难免，欢迎大家指出。

一、理论介绍

线性回归的预测函数：

\[y = w_1x_1+w_2x_2+...+w_nx_n+b
\]

写成向量的形式：$$y = \mathbf{w^Tx}+b $$

其中：\(\mathbf{w} = (w_1,...,w_n)^T,\mathbf{x}=(x_1,...,x_n)^T\)

为了编程方便，将\(b\)收缩到\(w\)向量里面去，有$$\mathbf{w} = (w_0,w_1,...,w_n)^T,w_0=b$$

\[\mathbf{x}=(x_0,x_1,...,x_n)^T,x_0=1
\]

上面模型变为$$y = \mathbf{w^Tx}$$

损失函数和偏导公式如下：

\[J（\mathbf{w}）=\frac{1}{2m} (\mathbf{Xw}-\mathbf{y} )^T(\mathbf{Xw}-\mathbf{y} )
\]

\[\frac{\partial J}{\partial \mathbf{w} } =\frac{1}{m} \mathbf{X^T} (\mathbf{Xw}-\mathbf{y} )
\]

有了以上的理论操作，下面可以开始操作了

【注】：上述理论推导本文不作说明，有需要可参考周志华老师西瓜书。

二、代码实现

1、导入库

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

库就不用介绍了，很常见的机器学习会用到的库。

2、准备数据集

生成数据集的方式很多，random库，或者你有数据（csv等）都可以。本文重点不是这个，因此简单用numpy手打生成了。

X_train = np.array([[2104, 5, 1, 45], [1416, 3, 2, 40], [852, 2, 1, 35]])
y_train = np.array([[460], [232], [178]])
print(X_train)
print(y_train)

输出结果：

注：我一般喜欢将向量是列向量还是行向量与数学公式中严格对应起来，否则，广播机制出现了问题真的很头疼的。

# 训练集第一列插入全为1的1列
new_column = np.ones((X_train.shape[0], 1))  # 创建一列全是 1 的数组
X_train = np.concatenate((new_column, X_train), axis=1)  # 在索引为 0 的位置插入新列
print(X_train)

3、定义预测函数（predict）

def predict(x,w):
    '''

    :param x: 要预测的样本点向量,x是行向量
    :param w: 训练出来的参数向量，w,是列向量
    :param b: 训练出来的参数 b ，b可以是标量，也可以是一个元素的数组
    :return: prediction,预测值
    '''
    return np.dot(x,w)

w_init = np.array([ [785.1811367994083],[0.39133535], [18.75376741], [-53.36032453], [-26.42131618]])
x_vec = X_train[0,:]
print(f"x_vec shape {x_vec.shape}, x_vec value: {x_vec}")

# make a prediction
f_wb = predict(x_vec,w_init)
print(f"f_wb shape {f_wb.shape}, prediction: {f_wb}")

输出：

4 代价（损失）函数

向量化加速：

\[J（\mathbf{w}，b ）=\frac{1}{2m} (\mathbf{Xw}-\mathbf{y} )^T(\mathbf{Xw}-\mathbf{y} )
\]

def loss(X,y,w):
    m = X.shape[0]
    err = np.dot(X,w) -y
    return (1/(2*m))*np.dot(err.T,err)

cost = loss(X_train, y_train, w_init)
print(f'Cost at optimal w : {cost}')

输出：

5 计算参数梯度

向量化加速：

\[\frac{\partial J}{\partial \mathbf{w} } =\frac{1}{m} \mathbf{X^T} (\mathbf{Xw}-\mathbf{y} )
\]

def compute_gradient(X, y, w):
    err = np.dot(X,w) - y
    return (1/len(X))*np.dot(X.T,err)

g = compute_gradient(X_train,y_train,w_init)
print(g)

输出：

6 批量梯度下降

def gradient_descent(X, y, w_in, loss, gradient_function, alpha, num_iters):
    J_history = []
    # 用来存每进行一次梯度后的损失，方便查看损失变化。如果要画损失变化也是用这个
    # w = copy.deepcopy(w_in)  #avoid modifying global w within function
    w = w_in

    for i in range(num_iters):
        dj_dw = gradient_function(X, y, w)
        w = w - alpha * dj_dw
        if i<100000:
            J_history.append( loss(X, y, w))
        if i % math.ceil(num_iters / 10) == 0:
            # 控制间隔 打印出一次损失结果
            # 总迭代次数分成均分10组，在每组最后打印一次损失
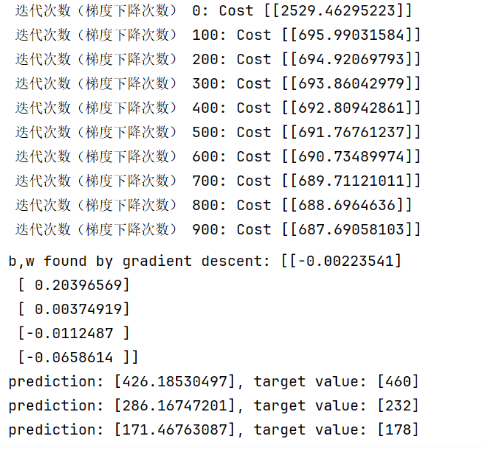
            print(f"迭代次数（梯度下降次数） {i}: Cost {J_history[-1]}")

    return w,J_history

7 训练

initial_w = np.zeros_like(w_init)
iterations = 1000
alpha = 5.0e-7
# run gradient descent
w_final,J_hist = gradient_descent(X_train, y_train, initial_w,loss, compute_gradient,
                                                    alpha, iterations)
print(f"b,w found by gradient descent: {w_final} ")
m = X_train.shape[0]
for i in range(m):
    print(f"prediction: {np.dot(X_train[i], w_final)}, target value: {y_train[i]}")

输出：

8 可视化一下损失

J_hist = [i[0,0] for i in J_hist]
# 画一下损失变化图
fig, (ax1, ax2) = plt.subplots(1, 2, constrained_layout=True, figsize=(12, 4))
ax1.plot(J_hist)
ax2.plot(100 + np.arange(len(J_hist[100:])), J_hist[100:])
ax1.set_title("Cost vs. iteration");  ax2.set_title("Cost vs. iteration (tail)")
ax1.set_ylabel('Cost')             ;  ax2.set_ylabel('Cost')
ax1.set_xlabel('iteration step')   ;  ax2.set_xlabel('iteration step')
plt.show()

输出：

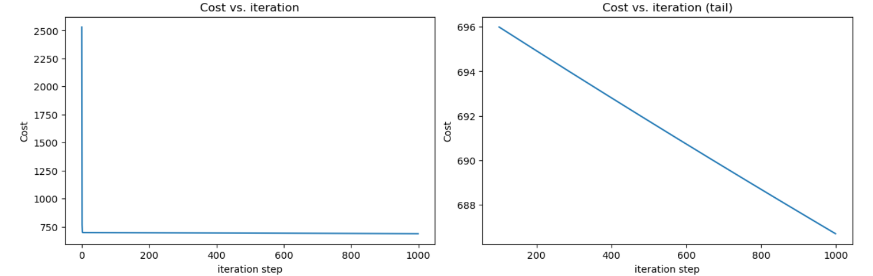
明显看到，随便取的数据集，\(loss\)迭代到后面就稳定600多了，线性回归不太适合该数据集。有时间在用多项式回归试试效果。

总结

以上就是基本的线性回归实现思路了，这里都是用矩阵向量化实现的，大家也可以试试迭代实现。后面有时间，我也会将迭代版本上传的。

【注】：需要\(jupyter\)源文件的可以评论区留言，看到我会回复的。

【注】：最后，作者实力有限，有错误在所难免，欢迎大家指出，会慢慢修改。