NOI 2023 题解

Copper Loser 的题解……

Day1 T1 方格染色

有一个 \(n\times m\) 的网格，有 \(Q\) 次操作，每次形如有三种：将 \((x_i+j,y_i)\)/\((x_i,y_i+j)\)/\((x_i+j,y_i+j)\) 染色，其中 \(j=0,1\dots L_i-1\)。 第三种操作至多只有 \(5\) 次，问之中有多少个格子被染过色。

扫描线板子题，首先令 \(ans=\sum\limits_{i=1}^QL_i\)，然后考虑如何去掉被重复染色的部分。

对于横线与竖线的，离散化之后使用扫描线求值即可。

由于斜线之后 \(O(1)\) 条，可以将每条斜线和所有其他线的交点算出来，然后去重即可。

时间复杂度 \(O(Q\log n)\)。

Day1 T2 桂花树

给定一棵有 \(n\) 个节点的树 \(T\)，保证一个节点的父亲编号小于它的编号。问有多少个有 \(n+m\) 的节点的树 \(T'\)，满足对于所有 \(1\le i<j\le n\) \(i,j\) 在 \(T\) 和 \(T'\) 上的最近公共祖先相同，对于所有 \(1\le i<j\le n+m\)，\(i\) 和 \(j\) 在 \(T'\) 中的最近公共祖先编号 \(\le \max(i,j)+k\)。

对于第一条限制，就确定了 \(T'\) 上 \(1,2\dots n\) 形成的虚树就是 \(T\)。

我们考虑从 \(T'\) 中逐个删除节点得到 \(T\) 的过程。

考虑特殊情况 \(k=0\)，则对于当前最大的节点 \(u\)，不存在 \(1\le i,j<u\)，\(i,j\) 的最近公共祖先为 \(u\)。这也就意味着 \(u\) 至多只有一棵子树，所以可以直接将这个点删去。

反转这个过程，也就意味这我们可以从小到大把节点插在一条树边上，或者挂在一个节点下面，成为它的儿子。假设当前大小为 \(siz\)，则一共有 \(2\times siz-1\) 种方案，所以这种情况的答案就是 \(\prod\limits_{i=1}^m(2n+2i-3)\)，可以直接 \(O(m)\) 计算。

这给了我们一个想法，对于当前要插入的节点其他的节点会是完全相同的，这也就意味着答案可能和 \(T\) 的形态无关，实际上确实是这样的。

考虑回到一般情况 \(k=10\)，仍然考虑从大到小删除，考虑当前最大的节点 \(u\)，由于限制被放宽了，所以它可能会存在若干个儿子。但是，由于公共祖先编号要 \(\le \max(i,j)+k\)，也就意味着它至多只有一个儿子的子树中存在编号 \(<u-k\) 的节点。那么，我们先跳过这个节点的删除，接着删除比它小的节点，由于上面的那一条限制，在删除到某一个编号 \(v \ge u-k\) 的节点时，\(u\) 只剩下一个儿子了，也就可以把 \(u\) 删除了。所以我们考虑在删除 \(v\) 的过程中同时删除掉 \(u\)。

不难发现 \(u\) 都会对应唯一的 \(v\)，\(v\) 也至多只能对应一个 \(u\)。

考虑反过来加入的过程，加入一个节点 \(u\) 时，可能会将一个 \(\le u+k\) 的节点作为父亲捆绑加入，而这种情况下，这一对点只能是放在一条树边上的。

设计 DP 状态 \(f_{i,S}\) 表示当前要加入 \(n+i\) 号节点，在 \(n+i\sim n+i+k-1\) 中已经被加入了的节点集合为 \(S\)。则最终的答案就是 \(f_{m+1,\varnothing}\)。

考虑转移：

如果 \(n+i\in S\)，说明 \(n+i\) 号节点已经被加入了，所以直接跳过，\(f_{i+1,S\setminus \{i\}}\gets f_{i,S}\)。

否则，我们可以按照正常的方式转移 \(n+i\)，也就是 \(f_{i+1,S}\gets f_{i,S}\times [2\times (n+i-1+|S|)-1]\)。

或者可以捆绑一个 \(v\in ([n+i+1,n+i+k]\cap \mathbb{N})\setminus S\) 的节点一起加入，转移为 \(f_{i+1,S\cup {v}}\gets f_{i,S}\times (n+i-1+|S|-1)\)。

时间复杂度 \(O(mk2^k)\)。

Day1 T3 深搜

一棵生成树 \(T\)，以及一个非树边边集 \(E\)，给定若干个关键点，问有多少个 \(E\) 的子集 \(E'\)，使得存在关键点 \(u\)，使得在 \(T\) 中加入 \(E'\) 中的所有边得到的图，\(T\) 可以是一个以 \(u\) 为根的 dfs 树。

是 dfs 树，也就意味着 \(E'\) 中所有的边都是返祖边，不是横插边。

一个边集 \(E'\) 可能对于多个关键点合法，考虑容斥。

设对于关键点集合 \(S\)，在以这个集合中任意一个点为根是，均是返祖边的边数量为 \(cnt(S)\)，则最终答案为 \(\sum\limits{S}(-1)^{|S|+1}2^{cnt(S)}\)。

考虑什么样的边会对点集 \(S\) 来说均是返祖边：

建出 \(S\) 点集在 \(T\) 上的虚树，则 \(E'\) 要么是虚树的一条树边，要么被虚树的一条虚边包含，要么就是一条不在虚树上的返祖边（在以某一个虚树或虚边上的点的子树内）。

钦定 \(1\) 为根，考虑在 \(S\) 所有点的 lca 处计算贡献，记 \(f_u\) 表示当前以 \(u\) 为根，只考虑子树内的边的所有情况的带符号和。记 \(d_u\) 为在 \(u\) 的子树外的返祖边数量（可能在以 \(1\) 为根时是横插边，但是以 \(u\) 为根是返祖边）。

则 \(u\) 最终对答案的贡献为 \(-f_u\times 2^{d_u}\)。

考虑如何转移，假设 \(v\) 为 \(u\) 的子树，\(f_v\) 向 \(f_u\) 的转移会带上很多从满足条件的边的贡献，具体的，就是满足上面说的两种情况的贡献，所以考虑事实维护一个数组 \(g_u\) 来处理这个贡献。不难知道 \(g_u\) 初始为 \(f_u\)。

如果有一条边 \((u,v_0)\)，则 \(v_0\) 的子树内所有的 \(g_u\) 变成 \(2\times g_u\)；将 \(u\) 向 \(fa_u\) 转移时，对于 \(u\) 某一个子树 \(v\) 内的所有返祖边 \(c_v\)，会将所有不在 \(v\) 子树内的点 \(g_u\) 变成 \(2^{c_v}\times g_u\)。

发现这些变化都是子树乘，可以通过对点的 dfs 序建线段树维护。

由于 \(u\) 只能从每一个子树内选择一个点转移，所以可以使用背包维护 \(dp_{0/1/2/3}\)。

最终的 \(f_u\)，如果 \(u\) 是关键点，则 \(f_u=-dp_0-dp_1-dp_2-dp_3+dp_2+dp_3=-dp_0-dp_1\)。

如果 \(u\) 不是关键点，则 \(f_u=dp_2+dp_3\)。

但是发现这样处理只能通过特殊性质 AB，也就意味着，有横插边对答案造成了影响。

我们发现，被漏算的部分，是 \(dp_2\) 的转移时，假设选择的子树为 \(v_1\) 和 \(v_2\)，同时没有选择点 \(u\)，这时横跨了 \(v_1,v_2\) 的横插边是会对答案做贡献的，具体如下图中的红边：

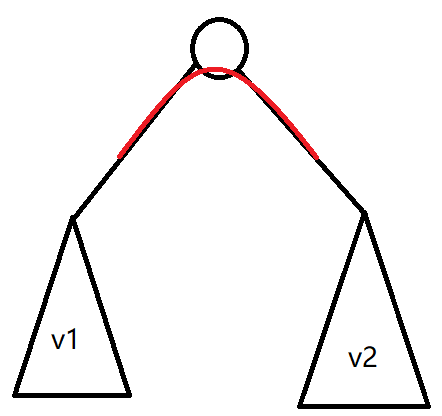
还是将子树拍成 dfs，则这样的每条边 \(u_0,u_1\)，都会对 \(v1\in[l_1,r_1],v2\in [l_2,r_2]\) 或 \(v2\in[l_1,r_1],v1\in [l_2,r_2]\) 的答案做贡献。

将每一对 \((v_1,v_2)\) 抽象成二维平面上的一个点，我们相当于要做若干次矩形乘和一次矩形和的操作。

对于每一个 \(u\)，把这样的操作离散化之后做一次扫描线即可。

总体复杂度 \(O((n+m)\log n)\)。

Day2 T1 贸易

给定一个带边权内向完全二叉树，同时给出若干条从祖先到子孙的边，定义 \(dis(x,y)\) 为 \(x\) 到 \(y\) 的最短路长度，求 \(\sum\limits_{x}\sum\limits_{y}dis(x,y)\)。

考虑处理出所有的 \(f_{x,y}\)，表示从祖先 \(x\) 走到子孙 \(y\) 的最短路，\(a_{y,x}\) 为从子孙 \(y\) 走到祖先 \(x\) 的距离，则最终 \(dis(u,v)\) 就等于 \(g_{u,lca}+f_{lca,v}\)，其中 \(lca\) 为 \(u,v\) 的最近公共祖先。

\(f_{x,y}\) 的值可以使用一个类似 floyd 的过程求出，\(g_{x,y}\) 可以直接通过树上差分得到。

最终求和是简单的。

总体复杂度 \(O(n^22^n)\)。

Day2 T2 字符串

给定一个字符串 \(S\)，多次询问 \(i,r\)，有多少个 \(1\le l\le i\)，使得 \(S[i,i+l-1]<S^T[i+l,i+2l-1]\)。

由于 \(S[i,i+l-1]<S^T[i+l,i+2l-1]\)，即 \(S[i,i+l-1]+S[i+l,i+2l-1]<S^T[i+l,i+2l-1]+S^T[i+l-1,i]\)，即 \(S[i,i+2*l-1]<S^T[i,i+2l-1]\)。

对于 \(S'=SS^T\)，上式等价于 \(S'[i,i+2l-1]<S'[2*n-(i+2l-1)+1,2*n-i+1]\)。

将 \(S'\) 后缀排序，上式在大多数情况下等价于 \(rk_i<rk_{2*n-(i+2l-1)+1}\)，从大往小扫 \(sa\) 数组，则对于每一个 \(i\),我们可以使用树状数组维护出做贡献的 \(l\)。

现在回到大多数情况下等价于的问题，我们会发现，当 \(S'[i,i+2l-1]=S'[2*n-(i+2l-1)+1,2*n-i+1]\) 的时候，它也可能有 \(rk_i<rk_{2*n-(i+2l-1)+1}\)。考虑怎么减去这种情况。

如果 \(S'[i,i+2l-1]=S'[2*n-(i+2l-1)+1,2*n-i+1]\)，就说明 \(S[i,i+2l-1]\) 是一个回文串，如果以 \(i+l+\frac{1}{2}\) 这个回文中心向外延伸，第一次不同的两个字符满足 \(c_{i+l+j-1}<c_{i+l-j}\)，则就会出现 \(rk_i<rk_{2*n-(i+2l-1)+1}\)，这个东西可以用 manacher 找出来，并再做一次扫描线求解。

时间复杂度 \(O(n\log n)\)。

Day2 T3 合并书本

有 \(n\) 堆书本，每一堆书本有两个参数 \((w_i,d_i)\)，初始时 \(w_i\) 给定，\(d_i=0\)。你需要进行 \(n-1\) 次合并，如果合并 \((w_1,d_1)\) 和 \((w_2,d_2)\)，则会消耗 \(w_2+d_1+d_2\) 的代价，得到一堆参数为 \((w_1+w_2,2\max(d_1,d_2)+1)\) 的书，要求最小化代价和。

发现合并的过程是一棵二叉树，对于 \(w\) 数组造成的代价，是每一个叶子节点到根的过程中作为右孩子的次数；对于 \(d\) 数组造成的贡献 \(D\)，只与树形态有关。

对于一棵二叉树，我们确定了每一个叶子在代价中的系数 \(a_i\)，则我们将所有的书本的 \(w\) 从小到大排序，所有的 \(a\) 从大到小排序，同时对位相乘即可。

现在的问题是我们要如何求出这个系数可重集 \(S\) 和 \(D\) 的关系。

考虑每次将若干叶子分裂的过程，那么我们会将集合中的若干个 \(x\) 变成 \(x\) 和 \(x+1\)。根据贪心策略可以得到，我们必然选择前若干小的叶子分裂。

但是这个时候我们发现 \(D\) 并不是很好计算，考虑如何维护分裂，反转成为合并考虑：每一次删去所有的叶子，每一次删除的叶子树是逐渐减少的。

所以考虑钦定分裂的叶子数 \(t\)，每一次分裂的叶子数量不会减少。这样每一次所有非叶子节点的代价都会 \(\times 2-1\)，所以可以直接计算。

发现这样的搜索十分优秀，可以通过此题。

代码