【LeetCode二叉树#00】二叉树的基础知识

基础知识

分类

满二叉树

如果二叉树中除了叶子结点，每个结点的度都为 2，则此二叉树称为满二叉树。

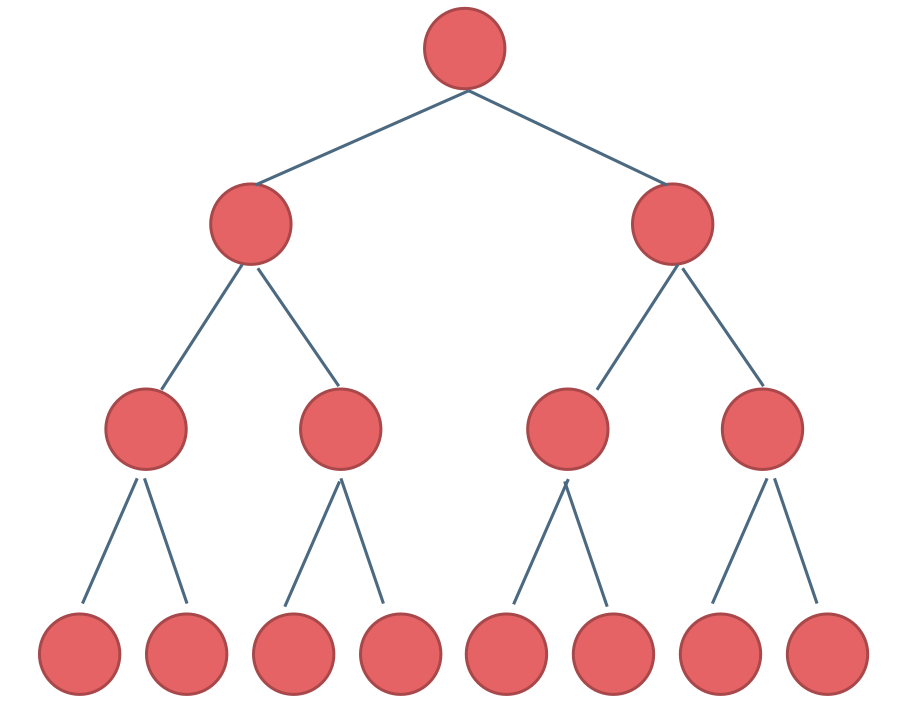
完全二叉树

除了底层外，其他部分是满的，且底层从左到右是连续的，称为完全二叉树

满二叉树一定是完全二叉树

举个例子：

完全二叉树

     1
    / \
   2   3
  / \ / \
 4  5 6

不是完全二叉树

     1
    / \
   2   3
  / \ / \
 4  5    6

二叉搜索树

例如：

     6
    / \
   3   9
  / \ / \
 1  4 8  10

二叉搜索树里面的节点是有顺序的

​ 左子树（左半边）的所有节点都小于中间节点

​ 右子树（右半边）的所有节点都大于中间节点

并且在左/右子树的子树中也满足该规律

平衡二叉搜索树

左子树和右子树高度差的绝对值不能大于1

什么意思呢？例如:

0      6
      /
1    3
    / \
2  1   4

上述二叉树不是平衡二叉搜索树

左子树的高度是2，右子树的高度是0，作差绝对值为2

再如：

0      6
      / \
1    3   9
    / \
2  1   4

这个就是平衡二叉搜索树

左子树的高度是2，右子树的高度是1，作差绝对值为1（右子树再加1个节点仍然还是）

又如：

0      6
      / \
1    3   9
    / \  /
2  1  4  8
  /
3 0

这个还是平衡二叉搜索树

其左子树本身（从3开始往下的）满足条件，整棵树的左右子树也满足条件

C++中map、set、multimap，multiset的底层实现都是平衡二叉搜索树，所以map、set的增删操作时间时间复杂度是logn，注意我这里没有说unordered_map、unordered_set，unordered_map、unordered_map底层实现是哈希表。

平时在使用容器时要有意识去了解其底层实现是什么数据结构（这样才知道所使用的数据结构中的元素是否有序、时间复杂度是多少、为什么）

存储方式

链式存储

如图所示

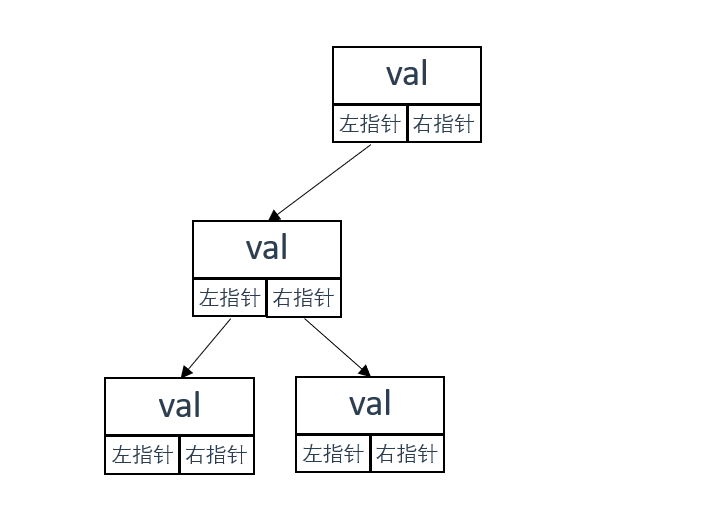
链式存储顾名思义就是使用指针（类似链表）的方式表示树

线性存储（了解）

其实就是用数组来存储二叉树，顺序存储的方式如图：

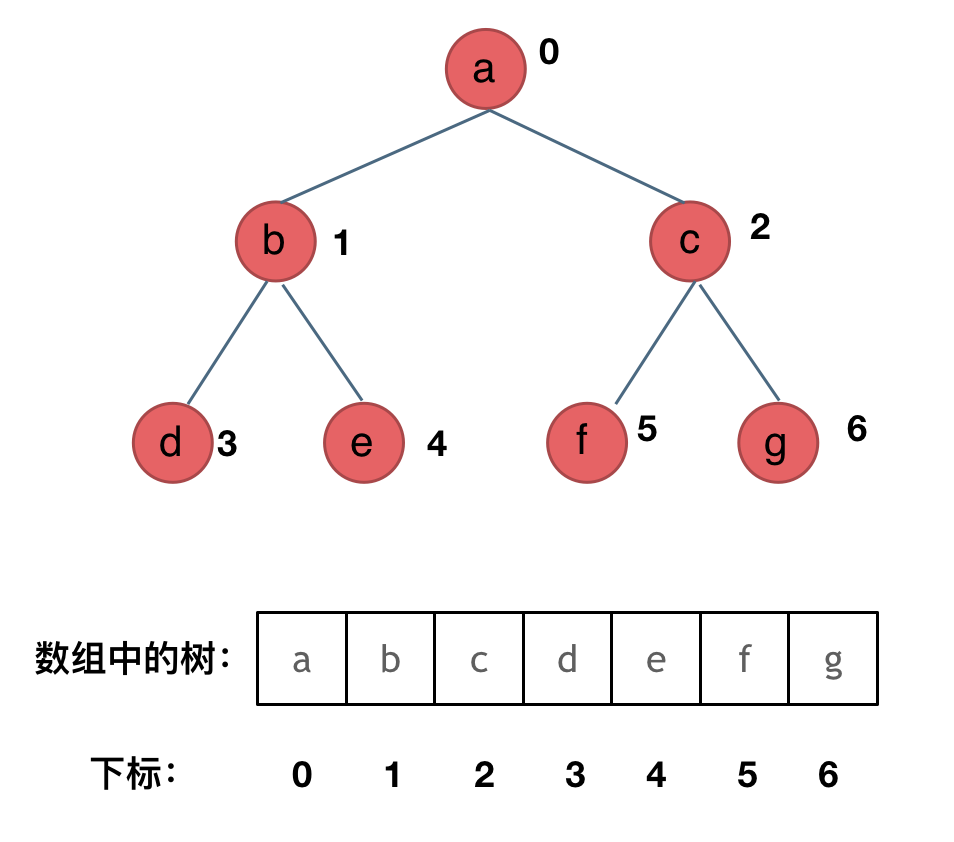
用数组来存储二叉树如何遍历的呢？

如果父节点的数组下标是 i，那么它的左孩子就是 i * 2 + 1，右孩子就是 i * 2 + 2。

但是用链式表示的二叉树，更有利于我们理解，所以一般我们都是用链式存储二叉树。

所以大家要了解，用数组依然可以表示二叉树。

注意（构造二叉树）

LeetCode上在做题时，二叉树通常是封装好的

但是实际面试的时候，有可能要手写待传入的数据。比如：请传入一个二叉树

因此，需要掌握构造一个二叉树的方法

平时做题的时候我们通常使用链式存储老保存一个二叉树

其实说白了就是一个链表，只不过这个链表的节点上有两个指针，分别指向左右子节点

（那就是双向链表咯）

于是，我们可以构造一个双向链表来表示一颗二叉树，在传入二叉树时将该链表的头结点传入即可

二叉树遍历方式

二叉树的遍历方式实际上对应与图论中的两种遍历方式：深度优先搜索和广度优先搜索

深度优先搜索

一般用 递归 的方式实现

前序遍历、中序遍历以及后序遍历均数据深度优先搜索

描述一下就是：在选定一个节点后，一直沿一跳路径搜索到末尾，然后递归回到最开始的位置再换方向继续搜索

当然使用非递归的方式也可以实现，一般使用 迭代法（即采用 栈 去模拟递归）

理论上，用递归解决的遍历问题都可以用相对应的迭代法解决（只是有些可能会麻烦一些）

（实际上计算机在实现递归时，底层就是用的栈）

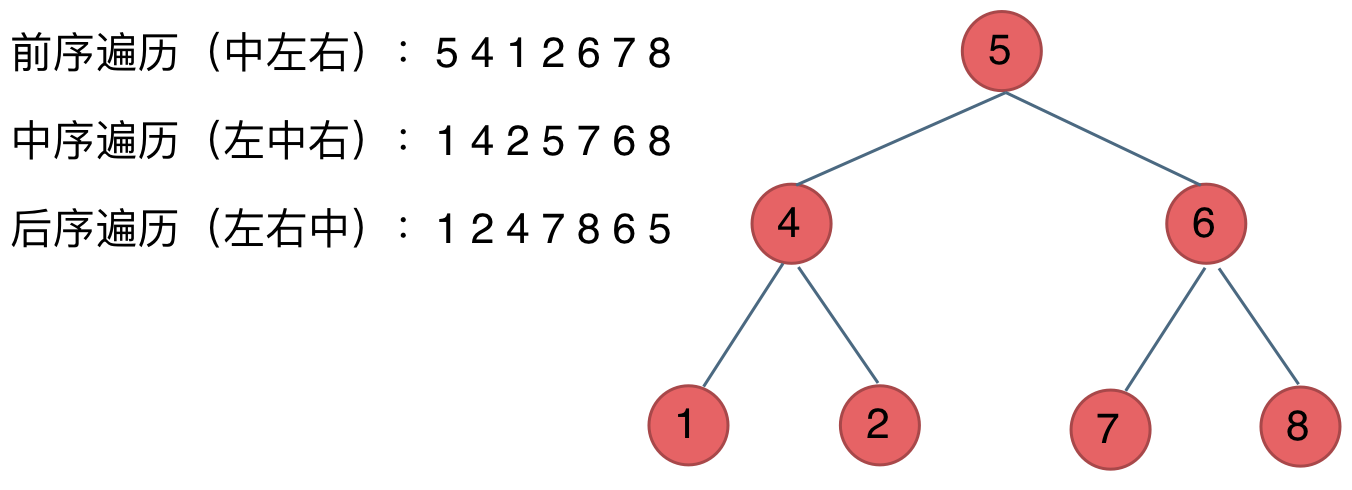
区分前/中/后序遍历

首先明确，这三种方式都是一条路先搜索到头再换方向的

那么他们的区别就是遍历时候的方向顺序

​ 前序：中左右

​ 中序：左中右

​ 后序：左右中

其实“前中后”描述的就是"中"的位置

例如：

广度优先搜索

通常指一层一层遍历二叉树的方式（在图论中是一圈一圈的遍历）

常见方法是：层序遍历

一般使用 队列 实现

二叉树定义方式

顺序存储就是用数组来存，这个定义没啥可说的，我们来看看链式存储的二叉树节点的定义方式。

C++代码如下：

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

二叉树的定义 和链表是差不多的，相对于链表 ，二叉树的节点里多了一个指针， 有两个指针，指向左右子节点。

**在现场面试的时候 面试官可能要求手写代码，所以数据结构的定义以及简单逻辑的代码一定要锻炼白纸写出来。