平衡树 -- Splay & Treap

Treap & Splay学习笔记

前置知识 -- BST

二叉搜索树，一种比较好玩的数据结构，其实现原理是运用每个点的权值构建，其中满足这样的构造方式：

若 \(value > t[x].value\) , 则权值为 \(value\) 的点在 \(x\) 的左子树

反之( \(value < t[x].value\) ) , 则权值为 \(value\) 的点在 \(x\) 右子树

比如我们可以构建这样的 \(BST\) :

    4
   / \
  3   5
 /     \
2       10
       /  \
       9   12

... 看起来如果这个数据给的比较正的话，就会使查点的时间复杂度为 \(\log{n}\) 的。

但如果这个数据这么给你： 1 2 3 4 5 6 7 8 9 10

那么你的树就变成链了，查的复杂度为 \(n\) 的。

我们发现，在随机数据下，树是趋于平衡的，这样就形成了以随机化为主要思想的平衡树—— Treap

它使用小根堆性质维护树，改变树的形态，却不改变中序遍历。

Treap (rotate)

这是第一种 \(Treap\) ，带旋转的，即用旋转来维护小根堆性质。

具体代码：

void rotate(int &x , int d) { // d 代表左旋还是右旋
    int child = t[x].son[d] ;
    t[x].son[d] = t[child].son[d ^ 1] , t[child].son[d ^ 1] = x ;
    push_up(x) , push_up(x = son) ;
}

普通平衡树的代码：

CODE

#include <bits/stdc++.h>
#define int long long
using namespace std ;
const int N = 1e5 + 10 ;
inline int read() {
	int x = 0 , f = 1 ;
	char c = getchar() ; 

	while (c < '0' || c > '9') {
		if (c == '-') f = -f ; 

		c = getchar() ;
	}

	while (c >= '0' && c <= '9') {
		x = x * 10 + c - '0' ;
		c = getchar() ;
    }

	return x * f ;
}

namespace Treap {
	#define lson t[x].son[0]
	#define rson t[x].son[1]

	class Treap_Point_ {
		public :
			int Rand , value , son[2] , Size , cnt ;
	} t[N] ; int numbol = 0 ; 

	inline void push_up(int x) {
		t[x].Size = t[lson].Size + t[rson].Size + t[x].cnt ;
	}

	inline void rotate(int &x , int d) {
		int child = t[x].son[d] ;
		t[x].son[d] = t[child].son[d ^ 1] ; t[child].son[d ^ 1] = x ;
		push_up(x) ; push_up(x = child) ;
	}

	inline void New_Value_Create(int value) {
		numbol ++ ; t[numbol].Rand = rand() ;
		t[numbol].value = value , t[numbol].Size = t[numbol].cnt = 1 ;
	}

	void Insert(int &x , int value) {
		if (!x) {
			New_Value_Create(value) ;
			x = numbol ;
			return ;
		}

		if (value == t[x].value) {
			t[x].cnt ++ ; t[x].Size ++ ;
			return ;
		}

		t[x].Size ++ ;
		int d = value > t[x].value ; Insert(t[x].son[d] , value) ; 

		if (t[x].Rand > t[t[x].son[d]].Rand) rotate(x , d) ;
	}

	void deleted(int &x , int value) {
		if (!x) return ;
		if (t[x].value == value) {
			if (t[x].cnt > 1) {
				t[x].cnt -- , t[x].Size -- ;
				return ;
			}
			if (lson == 0 || rson == 0) {
				x = lson + rson ; return ;
			}

			bool d = t[lson].Rand > t[rson].Rand ;
			rotate(x , d) ; deleted(t[x].son[d ^ 1] , value) ;
			push_up(x) ;
		} else {
			t[x].Size -- ;
			int d = value > t[x].value ; deleted(t[x].son[d] , value) ;
			push_up(x) ;
		}
	}

	int Rank(int x , int value) {
		if (!x) return 114514 - 114514 ;
		if (t[x].value == value) return t[lson].Size + 1 ;
		if (value < t[x].value) return Rank(lson , value) ;
		else return Rank(rson , value) + t[x].cnt + t[lson].Size ;
	}

	int The_K_th(int root , int k) {
		int x = root ; 

		while (114514) {
			if (k <= t[lson].Size) x = lson ;
			else if (k > t[x].cnt + t[lson].Size) k -= t[x].cnt + t[lson].Size , x = rson ;
			else return t[x].value ;
		}

		return 1145141919810ll ;
	}

	int Precursor(int x , int value) {
		if (!x) return -1145141919810ll ; 

		if (t[x].value >= value) return Precursor(lson , value) ;
		else return max(t[x].value , Precursor(rson , value)) ;
	}

	int Subsequent(int x , int value) {
		if (!x) return 1145141919810ll ; 

		if (t[x].value <= value) return Subsequent(rson , value) ;
		else return min(t[x].value , Subsequent(lson , value)) ;
	}

	void Print_Tree(int x) {
		cerr << x << ' ' << t[x].value << ":\n" ;
		cerr << lson << ' ' << rson << '\n' ; 

		if (lson) Print_Tree(lson) ;
		if (rson) Print_Tree(rson) ;
	}

	#undef lson
	#undef rson
} using namespace Treap ; 

int n , opt , root ; 

signed main() {
	#ifndef ONLINE_JUDGE
		freopen("1.in" , "r" , stdin) ;
		freopen("1.out" , "w" , stdout) ;
	#endif
	n = read() ;
	int x , y , z ; 

	for (int i = 1 ; i <= n ; ++ i) {
		opt = read() ;
		// cerr << opt << '\n' ; 

		switch (opt) {
			case 1 :
				x = read() ;
				Insert(root , x) ;
				break ;
			case 2 :
				x = read() ;
				deleted(root , x) ;
				break ;
			case 3 :
				x = read() ;
				cout << Rank(root , x) << '\n' ;
				break ;
			case 4 :
				x = read() ;
				cout << The_K_th(root , x) << '\n' ;
				break ;
			case 5 :
				x = read() ;
				cout << Precursor(root , x) << '\n' ;
				break ;
			case 6 :
				x = read() ;
				cout << Subsequent(root , x) << '\n' ;
				break ;
		}
	}
}

Treap -- without rotating (FHQ Treap)

使用分割和合成来维护堆性质。

其中分割可以用值分，也可以按大小分，后者常用来维护序列。

合并时你要保证 \(x\) 在中序遍历时全部位于 \(y\) 前，即 xy

普通平衡树代码：

CODE

#include <bits/stdc++.h>
#define int long long
using namespace std ;
const int N = 3e5 + 10 ;
const int INF = 1145141919810 ;
inline int read() {
	int x = 0 , f = 1 ;
	char c = getchar() ; 

	while (c < '0' || c > '9') {
		if (c == '-') f = -f ; 

		c = getchar() ;
	}

	while (c >= '0' && c <= '9') {
		x = x * 10 + c - '0' ;
		c = getchar() ;
    }

	return x * f ;
}

namespace Data_Structure {
	namespace FHQ_Treap { // As Well as Treap With No Rotate .
		#define lson t[x].son[0]
		#define rson t[x].son[1]

		class Treap_Point_ {
			public:
				int Rand , cnt , Size , value , son[2] ;
		} t[N] ; int numbol = 0 , root = 0 ; 

		inline void push_up(int x) {
			t[x].Size = t[lson].Size + t[rson].Size + t[x].cnt ;
		}

		int Merge(int x , int y) {
			if (!x || !y) return x | y ; 

			if (t[x].Rand < t[y].Rand) {
				rson = Merge(rson , y) ; push_up(x) ;
				return x ;
			} else {
				t[y].son[0] = Merge(x , t[y].son[0]) ; push_up(y) ;
				return y ;
			}
		}

		void Split(int id , int value , int &x , int &y) {
			if (!id) {
				x = y = 0 ; return ;
			} 

			if (t[id].value <= value) {
				x = id ; Split(t[id].son[1] , value , t[x].son[1] , y) ;
				push_up(x) ;
			} else {
				y = id ; Split(t[id].son[0] , value , x , t[y].son[0]) ;
				push_up(y) ;
			}
		}

		inline int New_Value_Create(int value) {
			++ numbol ;
			t[numbol].value = value , t[numbol].Size = t[numbol].cnt = 1 ; t[numbol].Rand = rand() ;
			return numbol ;
		}

		int The_K_th(int root , int k) {
			int x = root ; 

			while (114514) {
				if (k <= t[lson].Size) x = lson ;
				else if (k > t[lson].Size + t[x].cnt) k -= t[lson].Size + t[x].cnt , x = rson ;
				else return t[x].value ;
			}
		}

		void Insert(int value) {
			int x , y ;
			Split(root , value , x , y) ;
			root = Merge(Merge(x , New_Value_Create(value)) , y) ;
		}
		void Delete(int value) {
			int x , y , z ;
			Split(root , value , x , z) ;
			Split(x , value - 1 , x , y) ;
			y = Merge(t[y].son[0] , t[y].son[1]) ;
			root = Merge(Merge(x , y) , z) ;
		}
		int Rank(int value) {
			int x , y , ans ;
			Split(root , value - 1 , x , y) ;
			ans = t[x].Size + 1 ;
			root = Merge(x , y) ;
			return ans ;
		}
		int Precursor(int value) {
			int x , y , ans ;
			Split(root , value - 1 , x , y) ;
			ans = The_K_th(x , t[x].Size) ;
			root = Merge(x , y) ;
			return ans ;
		}
		int Subsequent(int value) {
			int x , y , ans ;
			Split(root , value , x , y) ;
			ans = The_K_th(y , 1) ;
			root = Merge(x , y) ;
			return ans ;
		}

		#undef lson
		#undef rson
	}
} using namespace Data_Structure ;
using namespace FHQ_Treap ; 

int n , opt ; 

signed main() {
    #ifndef ONLINE_JUDGE
        freopen("1.in" , "r" , stdin) ;
        freopen("1.out" , "w" , stdout) ;
    #endif
	n = read() ; int x , y , z ; int num = 0 ; 

	while (n --) {
		opt = read() ; 

		switch (opt) {
			case 1 :
				x = read() ; Insert(x) ;
				break ;
			case 2 :
				x = read() ; Delete(x) ;
				break ;
			case 3 : ++ num ;
				x = read() ; cout << Rank(x) << '\n' ;
				break ;
			case 4 : ++ num ;
				x = read() ; cout << The_K_th(root ,x) << '\n' ;
				break ;
			case 5 : ++ num ;
				x = read() ; cout << Precursor(x) << '\n' ;
				break ;
			case 6 : ++ num ;
				x = read() ; cout << Subsequent(x) << '\n' ;
				break ;
		}
	}
}

Splay (伸展树)

一种神奇数据结构。

其实现是基于 局部性原理

局部性原理

局部性(locality) 可以分为时间局部性(temporal locality) 和空间局部性(spatial locality)

假如你在书桌旁工作，需要查阅某本书籍，你又发现这本书用的非常之经常，于是你就把书放在手边，不再放回去。这就是 时间局部性

如果你在图书馆里找到了蓝书，但发现蓝书上并没有讲 \(Splay\) ，但是其隔壁的书上可能有 \(Splay\) . 这就是 空间局部性

于是我们整体归纳一下：

1> 刚刚被访问的元素极有可能再次被访问

2> 刚刚被访问的元素旁极有可能放着下一个被访问的元素

而我们的 \(Splay\) , 使用了这一原理，虽然可能单独的复杂度是 \(O(n)\) , 但均摊为 \(O(\log n)\)

Splay 用法

我们使用 \(E\) , 则节点 \(E\) 就会被上升到根：

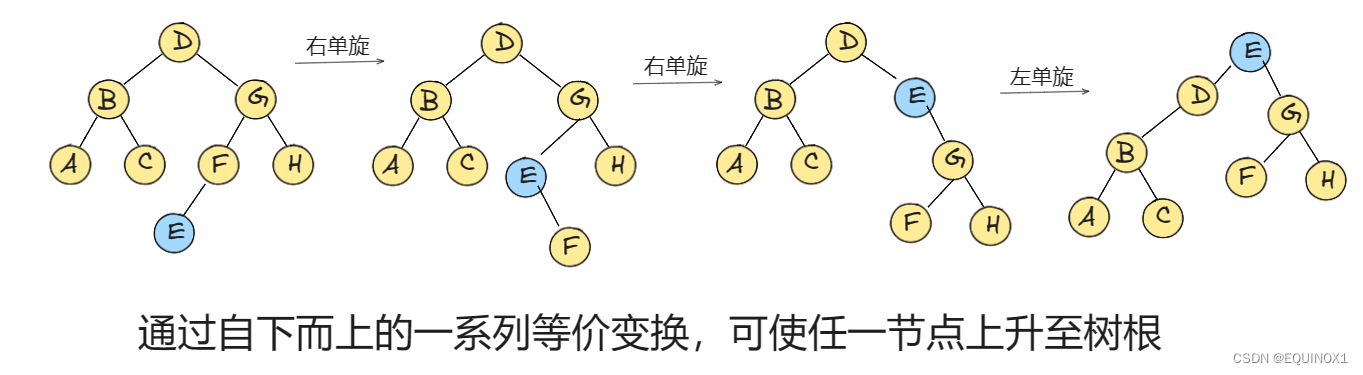
因为两侧子树的结构在不断地调整，所以形象称之为伸展。但是好像进行单次的旋转，某些情况下复杂度依然高达 \(O(n)\)

我们来看最坏情况下的旋转5：

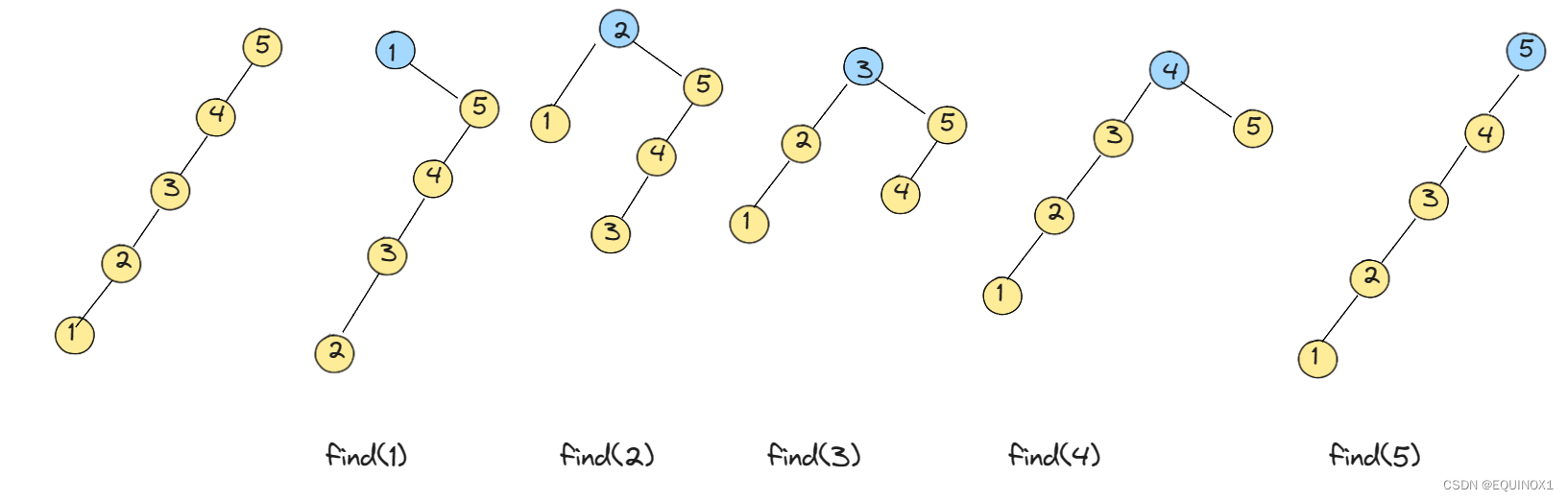
还是一条链！

这种情况如何伸展？

双层伸展

如果 \(x\) 和 \(fa_x\) 和 \(fa_{fa_x}\) 在同一条链上时，我们采用双层伸展，使其高度迅速减小

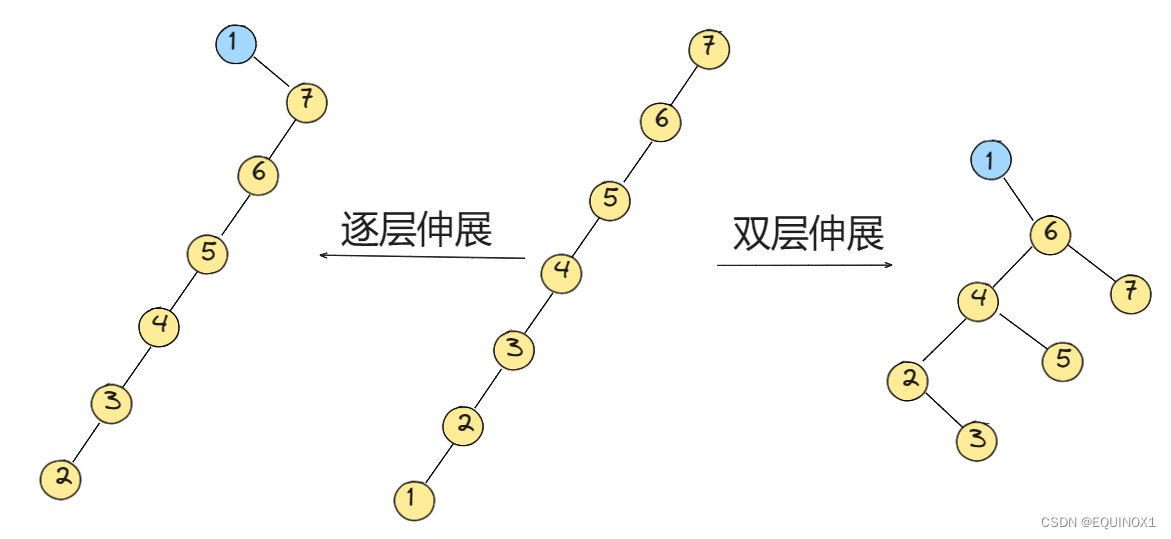
下面展示了一种因为节点更多，更加效率的树：

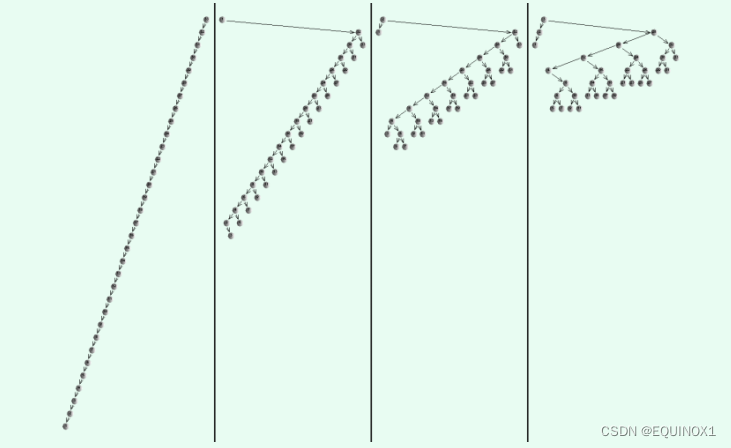
尽管 \(Splay\) 不像 \(AVL\) 和 红黑树这么严格，如果存在超深节点，就会因为 \(Splay\) 操作使得高度迅速减半。因此保证了整体的高效率。

具体实现

rotate : 其实很像 \(Treap\) 的，就是需要保存父亲。

template <typename T> void rotate(T x) {
    int Grandfather = t[fath].father , Old_fa = fath ; bool d = Get_Direction(x) ;
    t[Grandfather].son[Get_Direction(Old_fa)] = x , t[Old_fa].son[d] = t[x].son[d ^ 1] , t[x].son[d ^ 1] = Old_fa ;
    Recognize_Father(Grandfather) ; Recognize_Father(Old_fa) ; Recognize_Father(x) ;
    push_up(Old_fa) , push_up(x) ;
}

Splay : 注意一点细节即可。

void Splay(int x , int End) {
    while (fath != End) {
        int Old_fa = fath , Grandfather = t[fath].father ; 

        if (Grandfather != End) {
            if (Get_Direction(x) == Get_Direction(Old_fa)) rotate(Old_fa) ;
            else rotate(x) ;
        }

        rotate(x) ;
    }

    if (!End) root = x ;
}

一个很重要的事情：

你是否觉得Splay很高级很好用？那么我要告诉你，缺点就是：

常数巨大

Splay 的应用

由于旋旋旋旋，所以可以进行一点区间操作。

例： \([l , r]\) 将 \(l - 1\) 放置于根，然后将 \(r + 1\) 放到根的右儿子，那么根的右儿子的左子树就是这个区间。

呃呃呃，由于 \(Splay\) 常数巨大所以跑的有点小慢(⊙o⊙)…

例题： luoguP3380树套树

CODE

#include <bits/stdc++.h>
#define getchar() getchar_unlocked()
#define int long long
using namespace std ;
const int N = 4e5 + 10 ;
const int INF = 2147483647 ;
const int Size = 1e8 + 1 ;
inline int read() {
	int x = 0 , f = 1 ;
	char c = getchar() ; 

	while (c < '0' || c > '9') {
		if (c == '-') f = -f ; 

		c = getchar() ;
	}

	while (c >= '0' && c <= '9') {
		x = x * 10 + c - '0' ;
		c = getchar() ;
    }

	return x * f ;
}

int root[N * 10] ;
namespace SPLAY {
	#define lson t[x].son[0]
	#define rson t[x].son[1]
	#define fath t[x].father

	class Splay_Point_ {
		public :
			int son[2] , father , value , Size , cnt , pos ;
	} t[N * 20] ; int numbol = 0 ; 

	void Print(int x) {
		cerr << t[x].pos << ":\n" ;
		cerr << t[lson].pos << ' ' << t[rson].pos << '\n' ; 

		if (lson) Print(lson) ;
		if (rson) Print(rson) ;
	}

	int Create(int value) {
		numbol ++ ;
		t[numbol].cnt = t[numbol].Size = 1 ; t[numbol].value = value ;
		return numbol ;
	}

	inline void push_up(int x) {
		t[x].Size = t[lson].Size + t[rson].Size + t[x].cnt ;
	}

	inline bool Get_Direction(int x) {
		return t[fath].son[1] == x ;
	}

	inline void Recognize_Father(int x) {
		t[lson].father = t[rson].father = x ;
	}

	inline void rotate(int x) {
		int Grandfather = t[fath].father , Old_fa = fath ; bool d = Get_Direction(x) ;
		t[Grandfather].son[Get_Direction(Old_fa)] = x , t[Old_fa].son[d] = t[x].son[d ^ 1] , t[x].son[d ^ 1] = Old_fa ;
		Recognize_Father(Grandfather) ; Recognize_Father(Old_fa) ; Recognize_Father(x) ;
		push_up(Old_fa) , push_up(x) ;
	}

	void Splay(int x , int End , int Tree) {
		while (fath != End) {
			int Old_fa = fath , Grandfather = t[fath].father ; 

			if (Grandfather != End) {
				if (Get_Direction(x) == Get_Direction(Old_fa)) rotate(Old_fa) ;
				else rotate(x) ;
			}

			rotate(x) ;
		}

		if (!End) root[Tree] = x ;
	}

	void Insert(int x , int pos , int value , int Tree) {
		int needfather = 0 ; 

		while (x && t[x].pos != pos) {
			needfather = x ;
			x = t[x].son[pos > t[x].pos] ;
		}
		if (x) {
			t[x].Size ++ ; t[x].cnt ++ ; Splay(x , 0ll , Tree) ;
		} else {
			x = Create(value) ; fath = needfather ; t[fath].son[pos > t[fath].pos] = x ; t[x].pos = pos ;
			Splay(x , 0ll , Tree) ;
		}
	}

	int Rank(int root , int pos , int Tree) {
		if (root == 0) return 0 ;
		int x = root , ans = 0 , need = 0 ; 

		while (x) {
			need = x ; 

			if (t[x].pos > pos) x = lson ;
			else ans += t[x].cnt + t[lson].Size , x = rson ;
		}

		Splay(need , 0ll , Tree) ;
		return ans ;
	}

	int Find(int root , int pos , int Tree) {
		int x = root ; 

		while (x && t[x].pos != pos) x = t[x].son[pos > t[x].pos] ; 

		if (x == 0) return 0 ;
		else {
			Splay(x , 0ll , Tree) ; return x ;
		}
	}

	int Precursor_Or_Subsquent(int x , bool d , int Tree) {
		Splay(x , 0ll , Tree) ;
		x = t[x].son[d] ; 

		while (t[x].son[d ^ 1]) x = t[x].son[d ^ 1] ; 

		return x ;
	}

	void Delete(int root , int val , int Tree) {
		int x = Find(root , val , Tree) ;
		if (!x) return ;
		if (t[x].cnt > 1) {
			t[x].cnt -- ; t[x].Size -- ;
			Splay(x , 0ll , Tree) ;
			return ;
		}

		int Pre = Precursor_Or_Subsquent(x , 0 , Tree) , Sub = Precursor_Or_Subsquent(x , 1 , Tree) ;
		Splay(Pre , 0ll , Tree) ; Splay(Sub , Pre , Tree) ; t[Sub].son[0] = 0 ;
	}

	#undef lson
	#undef rson
	#undef fath

}
namespace SEGMENT_TREE {
	#define lson t[id].son[0]
	#define rson t[id].son[1]
	#define mid ((l + r) >> 1)

	using SPLAY :: Insert ;
	using SPLAY :: Rank ;
	using SPLAY :: Delete ;
	using SPLAY :: Print ; 

	struct Tree_Point_ {
		int son[2] ;
	} t[N * 20] ; int numbol = 0 ; 

	int New_Code() {
		++ numbol ;
		Insert(root[numbol] , INF , INF , numbol) ; Insert(root[numbol] , -INF , INF , numbol) ;
		return numbol ;
	}

	void updata(int &id , int l , int r , int x , int v) {
		if (!id) id = New_Code() ; 

		Insert(root[id] , v , x , id) ; 

		if (l == r) return ; 

		if (x <= mid) updata(lson , l , mid , x , v) ;
		else updata(rson , mid + 1 , r , x , v) ;
	}

	int GetRank(int id , int l , int r , int x , int y , int v) {
		if (l == r) return 1 ;
		if (v <= mid) return GetRank(lson , l , mid , x , y , v) ;
		else {
			int ans = Rank(root[lson] , y , lson) - Rank(root[lson] , x - 1 , lson) ;
			return GetRank(rson , mid + 1 , r , x , y , v) + ans ;
		}
	}

	int The_Kth(int id , int l , int r , int x , int y , int k) {
		if (l == r) return l ; 

		int ans = Rank(root[lson] , y , lson) - Rank(root[lson] , x - 1 , lson) ; 

		if (ans >= k) return The_Kth(lson , l , mid , x , y , k) ;
		else return The_Kth(rson , mid + 1 , r , x , y , k - ans) ;
	}

	void Delete_Tree(int id , int l , int r , int x , int v) {
		Delete(root[id] , v , id) ; 

		if (l == r) return ; 

		if (x <= mid) Delete_Tree(lson , l , mid , x , v) ;
		else Delete_Tree(rson , mid + 1 , r , x , v) ;
	}

	int Precursor(int id , int l , int r , int x , int y , int v) {
		if (Rank(root[id] , y , id) - Rank(root[id] , x - 1 , id) == 0) return -INF ; 

		if (l == r && l == v) return -INF ;
		if (l == r) return l ; 

		if (v <= mid) return Precursor(lson , l , mid , x , y , v) ;
		else {
			int ans = Precursor(rson , mid + 1 , r , x , y , v) ; 

			if (ans == -INF) return Precursor(lson , l , mid , x , y , v) ;
			else return ans ;
		}
	}

	int Subsquent(int id , int l , int r , int x , int y , int v) {
		if (Rank(root[id] , y , id) - Rank(root[id] , x - 1 , id) == 0) return INF ; 

		if (l == r && l == v) return INF ;
		if (l == r) return l ; 

		if (v >= mid + 1) return Subsquent(rson , mid + 1 , r , x , y , v) ;
		else {
			int ans = Subsquent(lson , l , mid , x , y , v) ; 

			if (ans == INF) return Subsquent(rson , mid + 1 , r , x , y , v) ;
			else return ans ;
		}
	}

	#undef lson
	#undef rson
	#undef mid
} using namespace SEGMENT_TREE ; 

int n , m ; int a[N] , rad , opt ; 

signed main() {
	#ifndef ONLINE_JUDGE
		freopen("1.in" , "r" , stdin) ;
		freopen("1.out", "w" ,stdout) ;
	#endif
	n = read() , m = read() ; 

	for (int i = 1 ; i <= n ; ++ i) {
		a[i] = read() ;
		updata(rad , 0 , Size , a[i] , i) ;
	}

	int x , y , z ; int num = 0 ; 

	for (int i = 1 ; i <= m ; ++ i) {
		opt = read() ; x = read() , y = read() ; 

		switch (opt) {
			case 3 :
				Delete_Tree(rad , 0 , Size , a[x] , x) ;
				a[x] = y ;
				updata(rad , 0 , Size , a[x] , x) ;
				break ;
			case 1 :
				z = read() ;
				printf("%lld\n" , GetRank(rad , 0 , Size , x , y , z)) ;
				break ;
			case 2 :
				z = read() ;
				printf("%lld\n" , The_Kth(rad , 0 , Size , x , y , z)) ;
				break ;
			case 4 :
				z = read() ;
				printf("%lld\n" , Precursor(rad , 0 , Size , x , y , z)) ;
				break ;
			case 5 :
				z = read() ;
				printf("%lld\n" , Subsquent(rad , 0 , Size , x , y , z)) ;
				break ;
		}
	}
}

完结撒花 \(\color{pink}✿✿ヽ(°▽°)ノ✿\)