excel多元回归-系数参数解读

sklearn实战-乳腺癌细胞数据挖掘

https://study.163.com/course/introduction.htm?courseId=1005269003&utm_campaign=commission&utm_source=cp-400000000398149&utm_medium=share

Excel多元回归

http://blog.sina.com.cn/s/blog_a20c88b601014j9x.html 转载

使用Excel数据分析工具进行多元回归分析与简单的回归估算分析方法基本相同。但是由于有些电脑在安装办公软件时并未加载数据分析工具，所以从加载开始说起（以Excel2010版为例，其余版本都可以在相应界面找到）。

点击“文件”，如下图：

在弹出的菜单中选择“选项”，如下图所示：

在弹出的“选项”菜单中选择“加载项”，在“加载项”多行文本框中使用滚动条找到并选中“分析工具库”，然后点击最下方的“转到”，如下图所示：

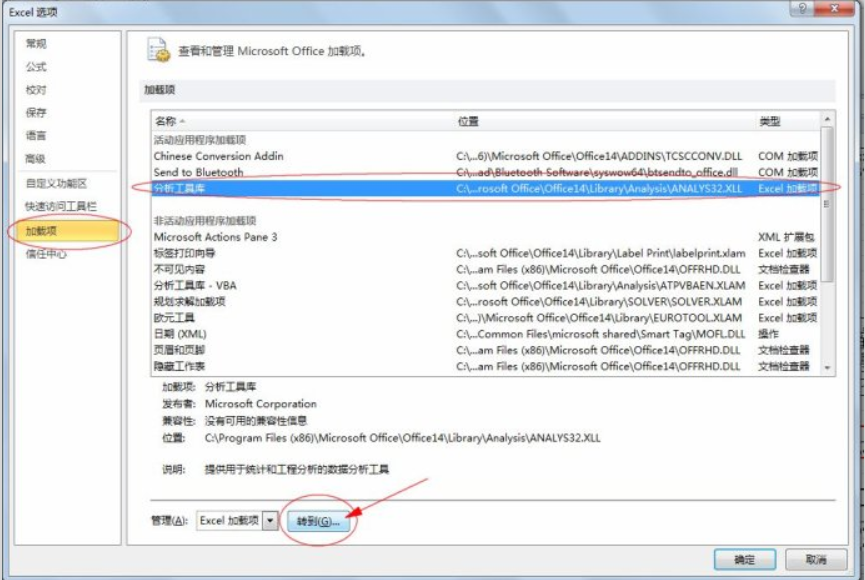
在弹出的“加载宏”菜单中选择“分析工具库”，然后点击 “确定”，如下图所示：

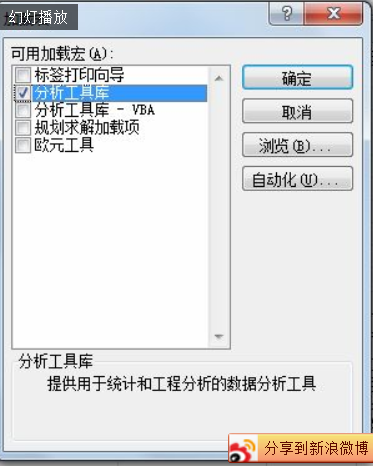
加载完毕，在“数据”工具栏中就出现“数据分析”工具库，如下图所示：

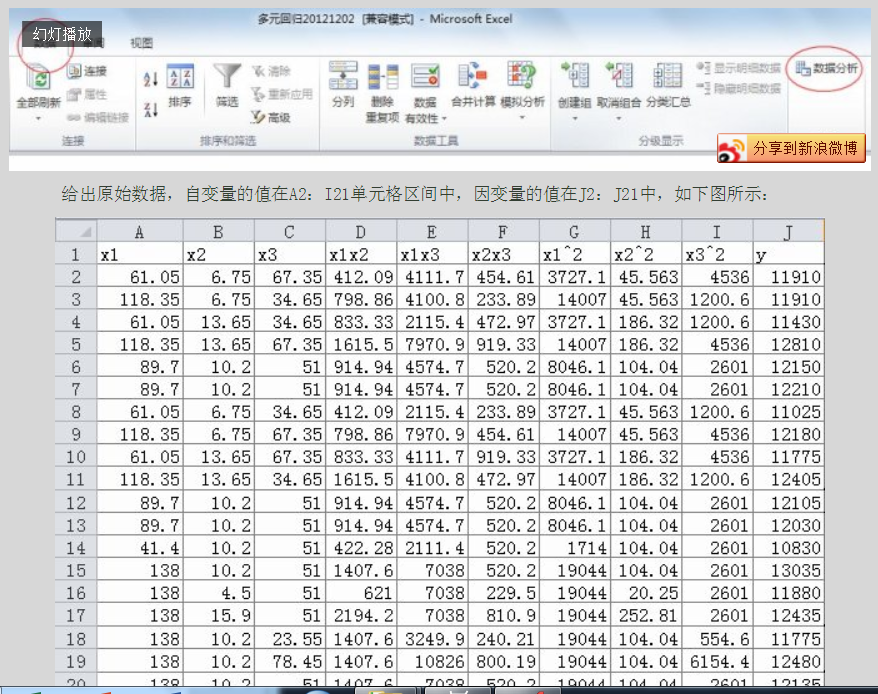
给出原始数据，自变量的值在A2：I21单元格区间中，因变量的值在J2：J21中，如下图所示：

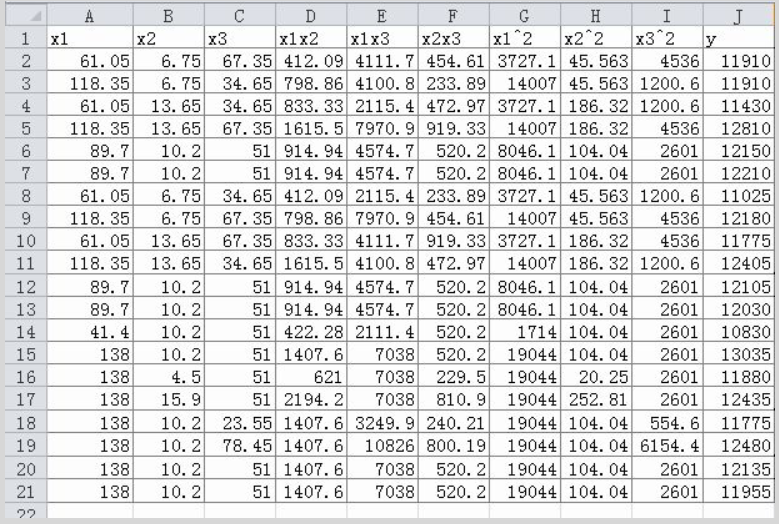
假设回归估算表达式为：

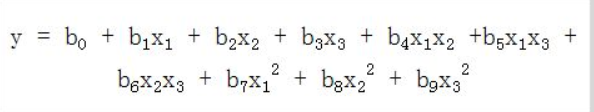
试使用Excel数据分析工具库中的回归分析工具对其回归系数进行估算并进行回归分析：

点击“数据”工具栏中中的“数据分析”工具库，如下图所示：

在弹出的“数据分析”-“分析工具”多行文本框中选择“回归”，然后点击 “确定”，如下图所示：

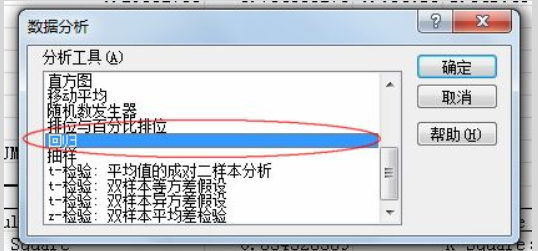
弹出“回归”对话框并作如下图的选择：

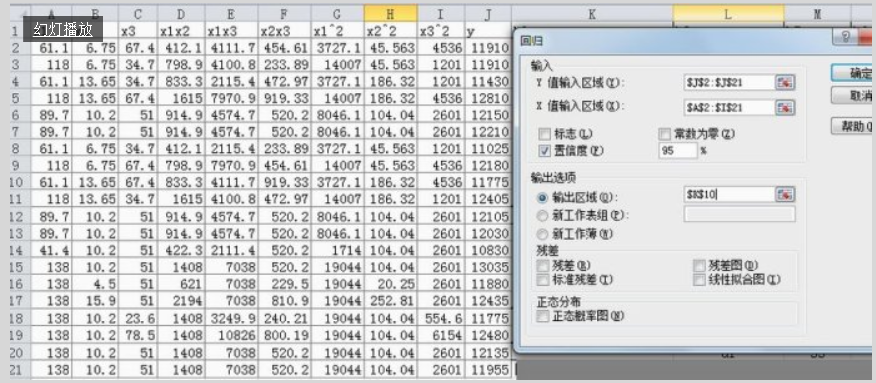
上述选择的具体方法是：

在“Y值输入区域”，点击右侧折叠按钮，选取函数Y数据所在单元格区域J2：J21，选完后再单击折叠按钮返回；这过程也可以直接在“Y值输入区域”文本框中输入J2：J21；

在“X值输入区域”，点击右侧折叠按钮，选取自变量数据所在单元格区域A2：I21，选完后再单击折叠按钮返回；这过程也可以直接在“X值输入区域”文本框中输入A2：I21；

置信度可选默认的95%。

在“输出区域”如选“新工作表”，就将统计分析结果输出到在新表内。为了比较对照，我选本表内的空白区域，左上角起始单元格为K10.点击确定后，输出结果如下：

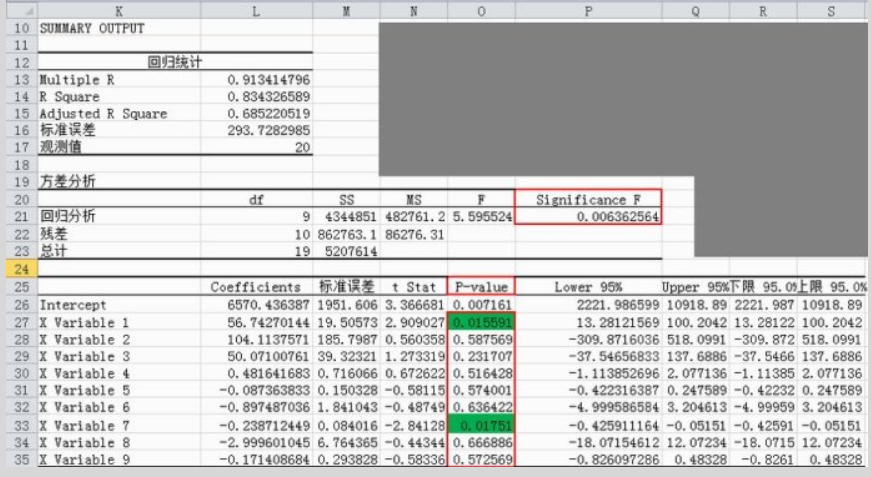
第一张表是“回归统计表”(K12：L17):

其中：

Multiple R：（复相关系数R）R²的平方根，又称相关系数，用来衡量自变量x与y之间的相关程度的大小。本例R=0.9134表明它们之间的关系为高度正相关。（Multiple：复合、多种）

R Square：复测定系数，上述复相关系数R的平方。用来说明自变量解释因变量y变差的程度，以测定因变量y的拟合效果。此案例中的复测定系数为0.8343，表明用用自变量可解释因变量变差的83.43%

Adjusted R Square：调整后的复测定系数R²，该值为0.6852，说明自变量能说明因变量y的68.52%，因变量y的31.48%要由其他因素来解释。（ Adjusted：调整后的）

标准误差：用来衡量拟合程度的大小，也用于计算与回归相关的其它统计量，此值越小，说明拟合程度越好

观察值：用于估计回归方程的数据的观察值个数。

第二张表是“方差分析表”：主要作用是通过F检验来判定回归模型的回归效果。

该案例中的Significance F（F显著性统计量）的P值为0.00636，小于显著性水平0.05，所以说该回归方程回归效果显著，方程中至少有一个回归系数显著不为0.（Significance：显著）

第三张表是“回归参数表”：

K26：K35为常数项和b1～b9的排序默认标示.

L26：L35为常数项和b1～b9的值，据此可得出估算的回归方程为：

该表中重要的是O列,该列的O26：O35中的 P-value为回归系数t统计量的P值。

值得注意的是：其中b1、b7的t统计量的P值为0.0156和0.0175，远小于显著性水平0.05，因此该两项的自变量与y相关。而其他各项的t统计量的P值远大于b1、b7的t统计量的P值，但如此大的P值说明这些项的自变量与因变量不存在相关性，因此这些项的回归系数不显著。