【拓扑 字符串还原 + 线段树维护】奇洛金卡达(father)

奇洛金卡达(father)

Description

阿良良木历将要迎来人生（不，是吸血鬼生涯）的第三次战斗——与身为
人类的奇洛金卡达在直江津高中的操场solo，以取回Heartunderblade 的左右
手。
奇洛金卡达。留着刺猬头、外形像神父的男子。靠着自身信仰，来消灭吸
血鬼的砖家。奇洛金卡达还是某个新兴宗教的大主教，那个宗教的教义，否定
了怪异的存在。
呐，在战斗之前，我们来研究一下那个新兴宗教的教义吧。教义被某种方
式加密成一个字符串，破译方式如下：
要按顺序执行n 个操作，第i 个操作由li,ri 两个正整数表示，意义为对
于当前字符串的[li,ri]区间，把其中编号为奇数的按顺序写下来，再在后面把
编号为偶数的按顺序写下来，最后把写出的新字符串加在区间后面。
为了更方便理解，举两个栗子：
1. s₁s₂s₃s₄s₅s₆s₇ l=3 r=5
操作后变成：s₁s₂s₃s₄s₅s₃s₅s₄s₆s₇
2. s₁s₂s₃s₄s₅s₆s₇ l=4 r=7

操作后变成：s₁s₂s₃s₄s₅s₆s₇s₅s₇s₄s₆
n 次操作后，可以得到一个新的字符串。这个字符串可能很长，为了方便，
奇洛金卡达把这个字符串的前k 个字符作为教义。现在给出加密后的字符串,k,
和n 个操作，你能求出教义吗？

Input
第一行一个字符串s，表示加密后的字符串。
接下来一行两个整数k,n，接下来n 行，每行两个整数l,r，表示这个操作的
li,ri

Output
一行，表示最终得到字符串的前k 个字符

Simple Example

# input1:
baka
17 5
1 4
1 4
10 10
10 10
10 12
# output1:
bakabkaabkkkkkkaa

Data Constraint

30%：k≤5000
70%：k≤200000
100%：0≤n≤5000 1≤k≤3000000 1≤li,ri≤10^9 且范围不会超过当前
字符串长度，字符串由大写、小写字母组成。数据保证初始字符串长度不大于
m，最终字符串长度不小于m

Solution：

• 我们要干什么（抽象出一个模型）

我们现在想知道原串S，经过n次操作后的处理串T，求T的前K位。

• 我们能干什么？（拿拿暴力分）

正序模拟（超过K不管），复杂度O(nk)，期望得分40-70

• 还能干什么？

好像不行了！！！

有没有想过这种题目正着优化很难，正难则反~~

我们手里有原串S，什么都没有了。

一个显然的事实是最后的T串所有字符都是S中出现过的。（而且是一些奇怪的规律）

好吧我们假装T串求出来了（比S串长的多！）

且把所有询问读入，倒序往前尝试复原。

、

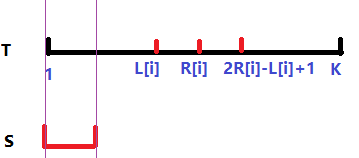考虑到T和S串前面length(S)位一定是相等的。而且后面的每一位都可以对应的从前面转移得到，

进一步的，后面所有的元素一定是T串前length(S)通过一定关系被指向的！那么我们只需要知道这样一个拓扑序，

就可以复原整个T串了！

• 1⁰当L[i]是奇数时。

　　　　 　　R[i]是奇数的时候：奇数的个数一定是 (R[i]-L[i])/2+1，偶数的个数一定是(R-L)/2,所以一定是这种情况：

R[i]是偶数的时候：奇数的个数一定是(R[i]-L[i]+1)/2，偶数的个数一定是(R[i]-L[i]+1)/2，所以一定是这种情况：

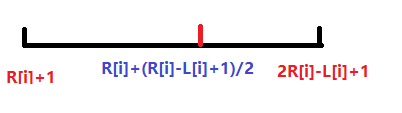
• 2⁰当L[i]是偶数时。

R[i]是奇数的时候：奇数的个数一定是 (R[i]-L[i]+1)/2，偶数的个数一定是(R[i]-L[i]+1)/2,所以一定是这种情况：

R[i]是奇数的时候：奇数的个数一定是  (R[i]-L[i])/2+1，偶数的个数一定是(R-L)/2,所以一定是这种情况：

结论：当L[i]和R[i]奇偶性相异的时候，是这样的情况：

当L[i]和R[i]奇偶性相同的时候，是这样的情况：

定义 qian[i]表示第i个位置是从第qian[i]个位置转移而来（就是qian[i]和i等值，i和qian[i]的映射是qian数组），

可以经过上述讨论求出这个qian[i]，一直求到最前端，然后一层层求出整个串T

然后我们发现通过上述处理后面的紫色到后面红色这一段是没有用的是不可能不知道，都可以从前面转移而来

将其删去。

我们定义线段树维护区间[l,r]中还有多少没有被删掉（可以被前面表示），

删去的话就是把从最后红色+1开始往后的所有元素区间减去要删数的个数（后面红色-中间紫色+1）

其实可以一个一个处理每次区间减-1！

最后按照拓扑序一个个还原就可以了！

# include<bits/stdc++.h>
using namespace std;
const int N=3e6+;
int t[*N],k,n;
int l[N],r[N],qian[N],ans[N];
char s[N];
void build(int x,int l,int r)
{
    t[x]=r-l+;
    if (l==r) return;
    int mid=(l+r)/;
    build(*x,l,mid);
    build(*x+,mid+,r);
}
int change(int x,int l,int r,int y,int z)
{
    int mid;
    while (l<r) {
        t[x]-=z;
        mid=(l+r)/;
        if (t[*x]<y) l=mid+,y-=t[*x],x=*x+;
        else r=mid,x=*x;
    }
    t[x]-=z;
    return l;
}
int p,q;
int main()
{
    scanf("%s",s+);
    scanf("%d%d",&k,&n);
    for (int i=;i<=n;i++) scanf("%d%d",&l[i],&r[i]);
    build(,,k);
    for (int j=n;j>=;j--) {
        if (r[j]>=t[]) continue;
        if (l[j]%==) p=l[j];
        else p=l[j]+;

         if (p>r[j]) {
            if (l[j]%==) p=l[j]+; else p=l[j];
         }
        for (int i=;i<=r[j]-l[j]+;i++) {
            if (r[j]>=t[]) continue;
            q=change(,,k,r[j]+,);
            qian[q]=change(,,k,p,);
            p+=;
            if (p>r[j]) {
                if (l[j]%==) p=l[j]+; else p=l[j];
            }
        }
     }
     int j=;
     for (int i=;i<=k;i++) {
        if (qian[i]) ans[i]=ans[qian[i]];else ans[i]=s[++j];
        putchar(ans[i]);
     }
     puts("");
    return ;
}