SPOJ11414 COT3 博弈论 + Trie树合并

---

考虑对于每个子树从下往上依次考虑

对于叶子节点而言，如果可以染色，那么其\(sg\)值为\(1\)，否则为\(0\)

考虑往上合并

如果选择了\(x\)，那么后继状态就是其所有子树

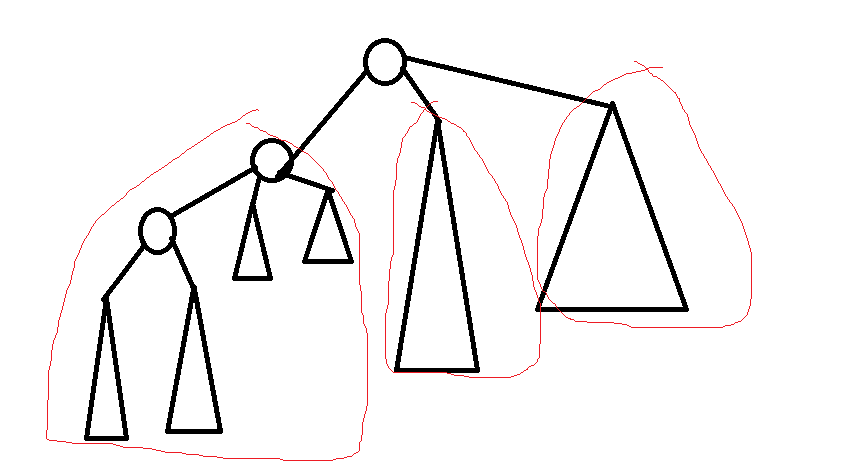
如果选了其他子树中的一点，那么后继状态的构成如图所示

也就是，到当前根为止的所有其他子树的\(sg\)值异或上本身

那么，我们可以考虑维护一个数据结构，每次往上的时候，对于一棵子树内的点，异或上其他子树的\(sg\)值

至于查\(sg\)值，可以用一个支持查\(mex\)的东西

还需要合并

\(Trie\)树是一个不错的选择

输出答案就随意\(dfs\)一下，思路和上面的差不多

复杂度\(O(n \log n)\)

---

#include <map>
#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;

#define ri register int
#define rep(io, st, ed) for(ri io = st; io <= ed; io ++)
#define drep(io, ed, st) for(ri io = ed; io >= st; io --)

const int sid = 2e5 + 5;
const int cid = 2e7 + 5;

#define gc getchar
inline int read() {
    int p = 0, w = 1; char c = gc();
    while(c > '9' || c < '0') { if(c == '-') w = -1; c = gc(); }
    while(c >= '0' && c <= '9') p = p * 10 + c - '0', c = gc();
    return p * w;
}

bool cov[cid];
int n, id, tot, cnp;
int q[sid], sg[sid], ls[cid], rs[cid], xr[cid];
int rt[sid], col[sid], cap[sid], nxt[sid], node[sid];

inline void addedge(int u, int v) {
    nxt[++ cnp] = cap[u]; cap[u] = cnp; node[cnp] = v;
}

inline void put_xor(int &o, int val, int dep) {
    if(dep <= -1) return;
    if(val & (1 << dep)) swap(ls[o], rs[o]);
    xr[o] ^= val;
}

inline void pushdown(int o, int dep) {
    if(!xr[o] || !o) return;
    put_xor(ls[o], xr[o], dep - 1);
    put_xor(rs[o], xr[o], dep - 1);
    xr[o] = 0;
}

inline void insert(int &o, int val, int dep) {
    if(!o) o = ++ id;
    if(dep == -1) { cov[o] = 1; return; }
    if(val & (1 << dep)) insert(rs[o], val, dep - 1);
    else insert(ls[o], val, dep - 1);
}

inline int merge(int x, int y, int dep) {
    if(!x || !y) return x + y;
    if(dep == -1) { cov[x] |= cov[y]; return x; }
    pushdown(x, dep); pushdown(y, dep);
    ls[x] = merge(ls[x], ls[y], dep - 1);
    rs[x] = merge(rs[x], rs[y], dep - 1);
    cov[x] = cov[ls[x]] && cov[rs[x]];
    return x;
}

inline int mex(int o, int dep) {
    if(!o || dep == -1) return 0;
    pushdown(o, dep);
    if(!cov[ls[o]]) return mex(ls[o], dep - 1);
    else return (1 << dep) + mex(rs[o], dep - 1);
}

#define cur node[i]
inline void dfs(int o, int fa) {
    int nsg = 0;
    for(int i = cap[o]; i; i = nxt[i])
        if(cur != fa) dfs(cur, o), nsg ^= sg[cur];
    if(!col[o]) insert(rt[o], nsg, 17);
    for(int i = cap[o]; i; i = nxt[i])
        if(cur != fa) {
            put_xor(rt[cur], nsg ^ sg[cur], 17);
            rt[o] = merge(rt[o], rt[cur], 17);
        }
    sg[o] = mex(rt[o], 17);
}

inline void find(int o, int fa, int SG) {
    for(int i = cap[o]; i; i = nxt[i])
        if(cur != fa) SG ^= sg[cur];
    if(SG == 0 && !col[o]) q[++ tot] = o;
    for(int i = cap[o]; i; i = nxt[i])
    if(cur != fa) find(cur, o, SG ^ sg[cur]);
}

int main() {
    n = read();
    rep(i, 1, n) col[i] = read();
    rep(i, 2, n) {
        int u = read(), v = read();
        addedge(u, v); addedge(v, u);
    }
    dfs(1, 0);
    find(1, 0, 0);
    if(tot) {
        sort(q + 1, q + tot + 1);
        rep(i, 1, tot) printf("%d\n", q[i]);
    }
    else puts("-1");
    return 0;
}