动态规划DP的斜率优化 个人浅解 附HDU 3669 Cross the Wall

首先要感谢叉姐的指导Orz

这一类问题的DP方程都有如下形式

dp[i] = w(i) + max/min(a(i)*b(j) + c(j)) （ 0 <= j < i ）

其中，b, c均为j的单调函数。通常情况下a(i)也是单调的，a(i)不单调时就只能二分查找了。

这里讲一下当c(j)单调递增，b(j)单调递减，原方程求min的情况

对于同一j，b(j)，c(j)为常数，而a(i)为变量，令y = b(j) * x + c(j)，则y为线性函数

我们把( 0 <= j < i )的直线均表示在平面上，则如下图所示。

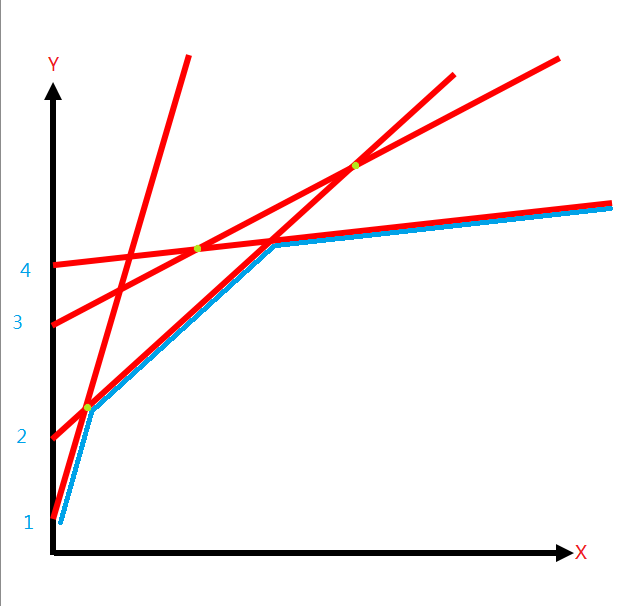
显然，对于不同的dp[i]，我们要求的是在对应x = a(i)下所有直线的最小值

看图我们可以发现，就是这些直线的下半平面交的边缘组成的分段函数，就是我们要求的函数

那么怎么维护这个半平面呢

首先b(j)最小的直线，必然会在足够大处，取得所有直线的最小值

我们在维护的过程中，总是在原半平面交的基础上，加上一个c(j)最大，b(j)最小的直线

这个时候，这条直线必然会加入半平面交当中。

同时，有可能会导致有些直线被遮蔽而退出集合。

我们可以发现，如果j=k的直线没有被遮蔽，那么j=[0,k)的直线也显然不会被遮蔽。

所以我们只需要从原来的半平面交最大的j开始不停的向内找，直到找到第一个没被遮蔽的直线就可以了。

那么直线什么时候会被遮蔽呢？

直线只剩两条的时候，显然不会有直线被遮蔽→ →

观察图中的直线1,2,3以及直线2,3,4。

2没有被遮蔽，是因为2和1的交点在2和3的交点左边。

而3被遮蔽，是因为3和2的交点在3和4的交点的右边。

所以只需要求交点然后比较大小就可以了。（两直线求交，初中知识，相信大家都会，请自行计算）

这里需要注意的是，求交点需要用到除法。但是除法容易出现精度问题，我们要把除法在比较的时候移到另一侧变成乘法，这个时候记得注意正负变号。

这个维护过程，考虑每个直线最多进出队列一次，复杂度总计O(n)

维护好半平面集合，后，求x = a(i)时的值，只需要二分判断落在哪个直线的交点区域内就好了。

特殊的，如果a(i)也单调，则可以像单调队里那样从头部一一剔除的方法，这里不多做介绍。

理解上述部分后，假如b(j),c(j)都不单调，问题则转变为动态半平面交。

另外，其实有没有发现写起来和凸包的理解非常像？叉姐告诉我们，其实根据平面的点与直线的对偶，凸包和半平面交问题是完全等价的。

附HDU 3669代码

 #include<cstdio>
 #include<cstring>
 #include<cmath>
 #include<cstdlib>
 #include<algorithm>
 using namespace std;
 typedef long long ll;
 const int N=;

 pair<int,int> a[N],s[N];
 int n,m;

 int l,r;
 pair<int,ll> q[N];

 int x,y;
 ll dp[][N];

 inline void push(int k,ll b){
     while(l<r && (q[r].second-q[r-].second)*(q[r].first-k)>=(b-q[r].second)*(q[r-].first-q[r].first)) r--;
     q[++r]=make_pair(k,b);
 }

 inline void pop(ll x){
     while(l<r && (q[l].first - q[l+].first)*x >= q[l+].second - q[l].second) l++;
 }

 int main(){
     while(~scanf("%d%d",&n,&m)){
         for(int i=;i<n;i++)scanf("%d%d",&a[i].first,&a[i].second);
         sort(a,a+n);
         int cnt=,mxb=a[n-].second;
         s[]=a[n-];
         for(int i=n-;i>=;i--)if(a[i].second>mxb){
             mxb = a[i].second;
             s[cnt++]=a[i];
         }
         n=cnt;
         ll mxa=s[].first;
         for(int i=;i<n;i++) dp[][i]=mxa*s[i].second;
         ll ans=dp[][n-];
         x=;
         y=;
         if(m>n) m=n;
         for(int k=;k<m;k++){
             l=;r=-;
             push(s[k].first,dp[x][k-]);
             for(int i=k;i<n;i++){
                 pop(s[i].second);
                 dp[y][i]=q[l].second+(ll)q[l].first*s[i].second;
                 push(s[i+].first,dp[x][i]);
             }
             x^=;
             y^=;
             if(dp[x][n-]<ans) ans=dp[x][n-];
             else break;
         }
         printf("%I64d\n",ans);
     }
     return ;
 }