【模板】平衡树——Treap和Splay

二叉搜索树（$BST$）：一棵带权二叉树，满足左子树的权值均小于根节点的权值，右子树的权值均大于根节点的权值。且左右子树也分别是二叉搜索树。（如下）

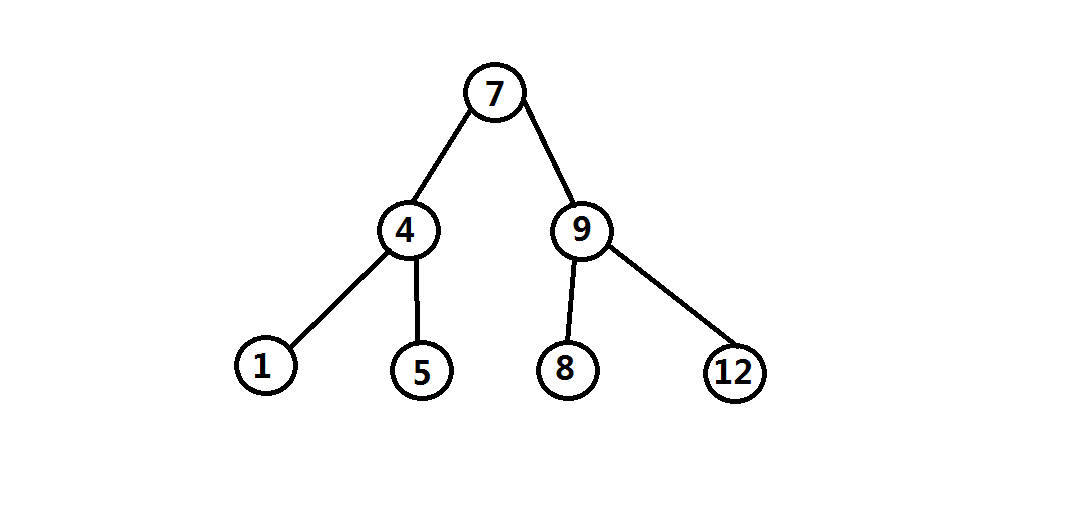
$BST$的作用：维护一个有序数列，支持插入$x$，删除$x$，查询排名为$x$的数，查询$x$的排名，求$x$的前驱后继等操作。

时间复杂度：$O(操作数\times 树深度)$。

也就是插入一个有序序列时复杂度稳定在$O(N^2)$……

平衡树：深度稳定在$O(log{节点数})$的$BST$。

使深度稳定的几种方法：增加一个破坏单调性的第二权值（$Treap$），每插入一个数进行旋转保持平衡（$Splay$），维护每个子树的$size$并使左右子树的$size$保持平衡（$SBT$）等。

本文主要给出$Treap$和$Splay$的实现方法。

---

$Treap$：顾名思义，该数据结构是$Tree$与$Heap$的结合体。

思想：在第一关键字满足$BST$性质的同时，为每个节点随机生成一个第二关键字，并通过旋转使得第二关键字满足堆性质。

旋转：（网上讲的很清楚了w）分为左右旋两种，如图（图源网络）：

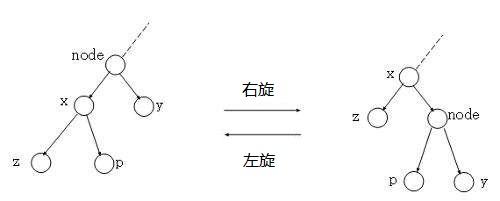
例如：（图源网络，图中点内是第一关键字【满足$BST$】，点外是随机生成的第二关键字【满足堆】）

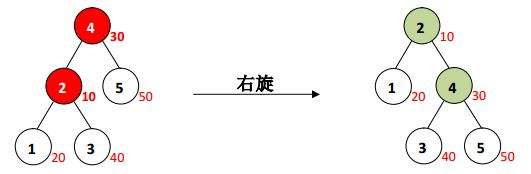
优点：常数小，实现简单。

缺点：应用范围较小，略有$0.001$%运气因素（能随机出来$10^5$个递增的数就可以去买彩票了w）

例题：bzoj3224普通平衡树

代码：

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<ctime>

using namespace std;
#define MAXN 100005
#define MAXM 500005
#define INF 0x7fffffff
#define ll long long

struct Treap{
    int l,r; //左儿子、右儿子
    int num,rnd; //该节点的第一关键字（权值）、该节点的第二关键字
    int cnt,siz; //该节点权值的出现次数、以该节点为根的子树的大小
}tr[MAXN];
int tot,root; //当前节点数、当前根节点 

inline int read(){
    int x=,f=;
    char c=getchar();
    for(;!isdigit(c);c=getchar())
        if(c=='-')
            f=-;
    for(;isdigit(c);c=getchar())
        x=x*+c-'';
    return x*f;
}

inline void update(int k){
    tr[k].siz=tr[k].cnt;
    tr[k].siz+=tr[tr[k].l].siz;
    tr[k].siz+=tr[tr[k].r].siz;
    return;
}
inline void zig(int &k){ //将以k为根的子树左旋（看图）
    int tp=tr[k].r;
    tr[k].r=tr[tp].l; //将k的右儿子置为k的右儿子的左儿子
    tr[tp].l=k; //将k的右儿子的左儿子置为k
    tr[tp].siz=tr[k].siz; //右儿子成为新的根，size等于k的size
    update(k); //更新k的size
    k=tp; //以k为根的子树变为以k的右儿子为根的子树，换根
    return;
}
inline void zag(int &k){ //将以k为根的子树右旋（同上）
    int tp=tr[k].l;
    tr[k].l=tr[tp].r;
    tr[tp].r=k;
    tr[tp].siz=tr[k].siz;
    update(k);
    k=tp;return;
}
inline void ins(int x,int &k){ //插入数x
    if(k==){ //当前节点为空则在此处新建节点
        k=++tot;
        tr[k].cnt=tr[k].siz=;
        tr[k].rnd=rand();
        tr[k].num=x;
        return;
    }
    tr[k].siz++; //插入的节点在该子树内，size+1
    if(x==tr[k].num) tr[k].cnt++; //如果该数已经出现过则不用新建节点，将该节点的cnt+1即可
    else if(x<tr[k].num){
        ins(x,tr[k].l); //x小于当前节点的关键字则插入当前节点的左子树
        if(tr[tr[k].l].rnd<tr[k].rnd) zag(k);
        //如果左儿子的第二关键字不满足小根堆性质就把左儿子转上来，容易证明此时一定满足堆性质
    }
    else{
        ins(x,tr[k].r); //x大于当前节点的关键字则插入当前节点的右子树
        if(tr[tr[k].r].rnd<tr[k].rnd) zig(k); //同上
    }
    return;
}

inline void del(int x,int &k){ //删除数x
    if(k==) return; //如果x没出现则返回
    if(x==tr[k].num){
        if(tr[k].cnt>) tr[k].cnt--,tr[k].siz--;
        //如果该节点出现次数>=1则不用移除节点，出现次数-1即可
        else if(tr[k].l*tr[k].r==)
            k=tr[k].l+tr[k].r;
        //如果该节点的儿子数<=1则可以直接删除，即拿它的儿子代替它
        else if(tr[tr[k].l].rnd<tr[tr[k].r].rnd) zag(k),del(x,k);
        else zig(k),del(x,k);
        //否则将该节点旋转到可以直接删除的位置再删除
        return;
    }
    tr[k].siz--; //删除的节点在该子树内，size-1
    if(x<tr[k].num) del(x,tr[k].l); //x在当前节点的左子树
    else del(x,tr[k].r); //x在当前节点的右子树
    return;
}

inline int qrnk(int x,int k){ //查询x数的排名（相当于查询有多少个数小于x）
    if(k==) return ;
    if(x==tr[k].num) return tr[tr[k].l].siz+;
    //找到了x，此时小于x的数的个数等于左子树的大小，排名需要+1
    else if(x<tr[k].num) return qrnk(x,tr[k].l);
    //x在当前节点的左子树中，直接递归左子树
    else return qrnk(x,tr[k].r)+tr[tr[k].l].siz+tr[k].cnt;
    //x在当前节点的右子树中，此时该节点及其左子树的权值均小于x，需要将这部分size加入答案
}

inline int qnum(int x,int k){ //查询排名为x的数
    if(k==) return ;
    if(tr[tr[k].l].siz<x && x<=tr[tr[k].l].siz+tr[k].cnt) return tr[k].num;
    //此时的排名正好确定在当前节点（大于等于当前节点的权值第一次出现的位置，小于等于该权值最后一次出现的位置），返回该节点的权值（第一关键字）即可
    else if(tr[tr[k].l].siz>=x) return qnum(x,tr[k].l);
    // 排名为x的数在当前节点的左子树中，直接递归
    else return qnum(x-(tr[tr[k].l].siz+tr[k].cnt),tr[k].r);
    //排名为x的数在当前节点的右子树中，此时该节点及其左子树不影响右子树中数的排名，需要减去这部分size
}

inline int qpre(int x,int k){ //查询x数的前驱（最大的小于x的数）
    if(k==) return -INF;
    if(x<=tr[k].num) return qpre(x,tr[k].l);
    //x在当前节点的左子树中，此时该节点不影响答案，递归左子树
    else return max(qpre(x,tr[k].r),tr[k].num);
    //x在当前节点的右子树中，此时该节点的权值小于等于x，又因为该节点的权值大于该节点左子树中的所有权值，将答案与k取max即可
}

inline int qnxt(int x,int k){ //查询x数的后继（最小的大于x的数），基本同上
    if(k==) return INF;
    if(x>=tr[k].num) return qnxt(x,tr[k].r);
    else return min(qnxt(x,tr[k].l),tr[k].num);
}

int main(){
    srand(time());
    int T=read();
    while(T--){
        int op=read(),x=read();
        switch(op){
            case :ins(x,root);break;
            case :del(x,root);break;
            case :printf("%d\n",qrnk(x,root));break;
            case :printf("%d\n",qnum(x,root));break;
            case :printf("%d\n",qpre(x,root));break;
            case :printf("%d\n",qnxt(x,root));break;
        }
    }return ;
}

---

$Splay$：又名旋转树，该数据结构通过巧妙的双旋&单旋($splay$)使树保持平衡。

基本思想：每次插入/查找一个节点时便将其旋转到根，在旋转过程中使树“看起来”逐渐平衡。

旋转：同上，双旋时注意若三点一线则需要转中间节点不然会失衡。（例如图中$1,2,4$节点需要先转$2$）

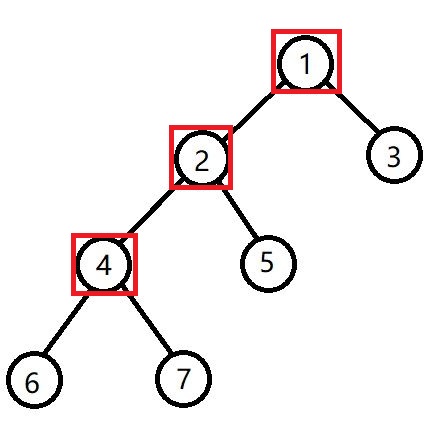
优点：使用范围很广，可以维护各种奇怪的区间操作。

缺点：实现复杂，常数较大，时间复杂度大概在$O(N\times log^2 N)$左右。严格证明我也不会

例题：同上。

代码：（某同学没有要求就不加注释了，需要注释可以@我w）

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>

using namespace std;
#define MAXN 100005
#define MAXM 500005
#define INF 0x7fffffff
#define ll long long

struct node{
    int v,f,siz,cnt,ch[];
}tr[MAXN];
int rt,tot;

inline int read(){
    int x=,f=;
    char c=getchar();
    for(;!isdigit(c);c=getchar())
        if(c=='-')
            f=-;
    for(;isdigit(c);c=getchar())
        x=x*+c-'';
    return x*f;
}

inline bool getf(int k){return tr[tr[k].f].ch[]==k;}
inline void update(int k){
    tr[k].siz=tr[k].cnt;
    tr[k].siz+=tr[tr[k].ch[]].siz;
    tr[k].siz+=tr[tr[k].ch[]].siz;
    return;
}
inline void clear(int k){
    tr[k].v=tr[k].f=;
    tr[k].ch[]=tr[k].ch[]=;
    tr[k].siz=tr[k].cnt=;
    return;
}
inline void rotate(int k){
    int f1=tr[k].f,f2=tr[f1].f;bool d=getf(k);
    tr[f1].ch[d]=tr[k].ch[d^];tr[tr[k].ch[d^]].f=f1;
    tr[k].ch[d^]=f1;tr[f1].f=k;tr[k].f=f2;
    if(f2) tr[f2].ch[tr[f2].ch[]==f1]=k;
    update(f1);update(k);return;
}
inline void splay(int k){
    for(int fa;fa=tr[k].f;rotate(k))
        if(tr[fa].f)
            rotate(getf(k)==getf(fa)?fa:k);
    rt=k;return;
}
inline int qrnk(int x){
    int now=rt,ans=;
    while(){
        if(x==tr[now].v){
            ans+=tr[tr[now].ch[]].siz+;
            splay(now);return ans;
        }
        else if(x<tr[now].v) now=tr[now].ch[];
        else ans+=tr[tr[now].ch[]].siz+tr[now].cnt,now=tr[now].ch[];
    }
}
inline int qnum(int x){
    int now=rt;
    while(){
        if(tr[tr[now].ch[]].siz<x && tr[tr[now].ch[]].siz+tr[now].cnt>=x)
            return tr[now].v;
        else if(tr[tr[now].ch[]].siz>=x) now=tr[now].ch[];
        else x-=tr[tr[now].ch[]].siz+tr[now].cnt,now=tr[now].ch[];
    }
}
inline int qpre(){
    int now=tr[rt].ch[];
    while(tr[now].ch[]) now=tr[now].ch[];
    return now;
}
inline int qnxt(){
    int now=tr[rt].ch[];
    while(tr[now].ch[]) now=tr[now].ch[];
    return now;
}
inline void ins(int x){
    if(!rt){
        tr[++tot].v=x,tr[tot].f=;
        tr[tot].ch[]=tr[tot].ch[]=;
        tr[tot].siz=tr[tot].cnt=;
        rt=tot;return;
    }
    int now=rt,fa=;
    while(){
        if(x==tr[now].v){
            tr[now].cnt++;
            update(now);update(fa);
            splay(now);break;
        }
        fa=now;now=tr[now].ch[x>tr[now].v];
        if(!now){
            tr[++tot].v=x,tr[tot].f=fa;
            tr[tot].ch[]=tr[tot].ch[]=;
            tr[tot].siz=tr[tot].cnt=;
            tr[fa].ch[x>tr[fa].v]=tot;
            update(fa);splay(tot);
            break;
        }
    }
    return;
}
inline void del(int x){
    qrnk(x);
    if(tr[rt].cnt>) tr[rt].cnt--,update(rt);
    else if(!tr[rt].ch[] && !tr[rt].ch[]) clear(x),rt=;
    else if(!tr[rt].ch[]){
        int tp=rt;rt=tr[rt].ch[];
        tr[rt].f=;clear(tp);
    }
    else if(!tr[rt].ch[]){
        int tp=rt;rt=tr[rt].ch[];
        tr[rt].f=;clear(tp);
    }
    else{
        int tp=rt;splay(qpre());
        tr[rt].ch[]=tr[tp].ch[];
        tr[tr[tp].ch[]].f=rt;
        update(rt);clear(tp);
    }
    return;
}

int main(){
    int T=read();
    while(T--){
        int opt=read(),x=read();
        switch(opt){
            case :ins(x);break;
            case :del(x);break;
            case :printf("%d\n",qrnk(x));break;
            case :printf("%d\n",qnum(x));break;
            case :ins(x);printf("%d\n",tr[qpre()].v);del(x);break;
            case :ins(x);printf("%d\n",tr[qnxt()].v);del(x);break;
        }
    }
    return ;
}