【模板】区间第k小

【模板】区间第k小

我实在是太弱了现在才会这个东西QAQ。

主席树做法。

一张关于主席树的无字说明

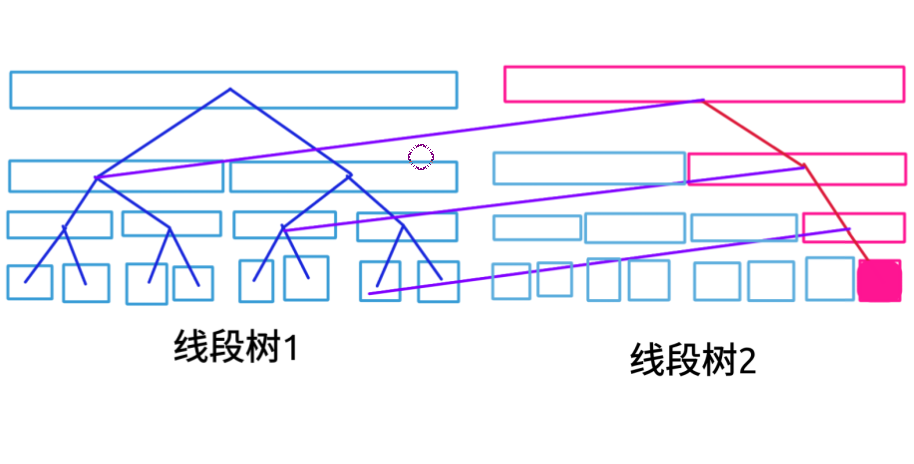
线段树\(2\)是只单点修改了实心酒红色点的线段树\(2\)，线段树\(2\)中的蓝色节点实际上就是线段树\(1\)的蓝色节点，我们只是把地址复制过来了。

我们多开了一个线段树，但是节点数量却只多了\(log\)层，那么对于\(n\)的历史版本保留就提供了\(O(nlogn)\)的数据结构啦。

具体代码怎么实现？我研究了一下，发现实际写出来的代码和大家常写的代码是一样的。实现其实非常简单，只需要在普通线段树上稍微修改一下。

如何访问历史版本？我们可以开一个\(rt(i)\)数组表示\(i\)号版本的根节点的编号，对于线段树每个节点我们要记录\(seg_L,seg_R,data\)，递归时只要访问\(seg_{L/R}\)的值就好了，不需要很大的修改。

其实我还想问一个问题，就是我发现这种主席树支持单点修改，区间查询，但是我想问如果是区间修改，而且是\(n\times n\)的修改怎么办？因为我发现修改一个点就一定会产生新的\(n\)个节点了。

实际上主席树就是让整个线段树有了两维下标，所以对于什么二维数点啊什么什么之类的也有用。

这个问题以后再解决，那么有了主席树工具之后怎么解此题？

不是两维下标吗？建立一个下标是值域和位置的线段树(按照给的序列的顺序建立主席树，主席树存储的东西是值域内有多少个数)，然后区间的限制可以直接是\(rt_R-rt_{L-1}\)很方便地查询。

实际上，主席树教会我们如何弄一个可持久化数组！有了可持久化数组，什么可持久化数据结构不行！平衡树呢:)

#include<bits/stdc++.h>

using namespace std;typedef long long ll;
#define RP(t,a,b)  for(register int t=(a),edd=(b);t<=edd;++t)
#define midd register int mid=(l+r)>>1
#define TMP template < class ccf >
#define lef l,mid,seg[pos].l
#define rgt mid+1,r,seg[pos].r
TMP inline ccf qr(ccf b){
    register char c=getchar();register int q=1;register ccf x=0;
    while(c<48||c>57)q=c==45?-1:q,c=getchar();
    while(c>=48&&c<=57)x=x*10+c-48,c=getchar();
    return q==-1?-x:x;}
TMP inline ccf Max(ccf a,ccf b){return a<b?b:a;}
TMP inline ccf Min(ccf a,ccf b){return a<b?a:b;}
TMP inline ccf Max(ccf a,ccf b,ccf c){return Max(a,Max(b,c));}
TMP inline ccf Min(ccf a,ccf b,ccf c){return Min(a,Min(b,c));}
TMP inline void READ(ccf* _arr,ccf* _b,int _n){RP(t,1,_n) _b[t]=_arr[t]=qr((ccf)1);}
//----------------------template&IO---------------------------
#define pushup(pos) (seg[pos].data=seg[seg[pos].l].data+seg[seg[pos].r].data)
const int maxn=2e5+5;
struct SEG{int l,r,data;}seg[maxn*81];//log2e5=17  ,  17*4=75

int rt[maxn];int data[maxn],sav[maxn];int sz,cnt;
int n,m;

void build0(int l,int r,int pos){
    if(l==r)return;midd;
    seg[pos].l=++cnt;seg[pos].r=++cnt;
    build0(lef);build0(rgt);
}

void build(int last,int k,int l,int r,int pos){
    if(l==r)  { seg[pos].data=seg[last].data+1; return; }midd;
    if(k<=mid){seg[pos].l=++cnt;seg[pos].r=seg[last].r;build(seg[last].l,k,lef);}
    else      {seg[pos].l=seg[last].l;seg[pos].r=++cnt;build(seg[last].r,k,rgt);}
    pushup(pos);
}

int a(int L,int R,int l,int r,int k){
    if(l>=r) return l;
    register int t=seg[seg[R].l].data-seg[seg[L].l].data;midd;
    if(t>=k) return a(seg[L].l,seg[R].l,l,mid,k);
    else return a(seg[L].r,seg[R].r,mid+1,r,k-t);
}

int main(){
#ifndef ONLINE_JUDGE
    freopen("in.in","r",stdin);
    freopen("out.out","w",stdout);
#endif
    n=qr(1);m=qr(1);
    READ(data,sav,n);
    sort(sav+1,sav+n+1);
    sz=unique(sav+1,sav+n+1)-sav-1;
    RP(t,1,n) data[t]=lower_bound(sav+1,sav+sz+1,data[t])-sav;
    cnt=rt[0]=1;build0(1,sz,1);
    RP(t,1,n){rt[t]=++cnt;build(rt[t-1],data[t],1,sz,rt[t]);}
    RP(t,1,m){
	register int t1,t2,t3;
	t1=qr(1);t2=qr(1);t3=qr(1);
	printf("%d\n",sav[a(rt[t1-1],rt[t2],1,sz,t3)]);
    }
    return 0;
}

还有一道模板题，也放进来吧

#include<bits/stdc++.h>

using namespace std;typedef long long ll;
#define DRP(t,a,b) for(register int t=(a),edd=(b);t>=edd;--t)
#define RP(t,a,b)  for(register int t=(a),edd=(b);t<=edd;++t)
#define ERP(t,a)   for(register int t=head[a];t;t=e[t].nx)
#define midd register int mid=(l+r)>>1
#define TMP template < class ccf >
#define lef l,mid,sL[pos]
#define rgt mid+1,r,sR[pos]
const int maxn=1e6+5;
char buf[maxn], *p1, *p2;
inline char gc() { return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, maxn, stdin), p1 == p2) ? EOF : *p1++; }
TMP inline ccf qr(ccf b){
    register char c=gc();register int q=1;register ccf x=0;
    while(c<48||c>57)q=c==45?-1:q,c=gc();
    while(c>=48&&c<=57)x=x*10+c-48,c=gc();
    return q==-1?-x:x;}
TMP inline ccf Max(ccf a,ccf b){return a<b?b:a;}
TMP inline ccf Min(ccf a,ccf b){return a<b?a:b;}
TMP inline ccf Max(ccf a,ccf b,ccf c){return Max(a,Max(b,c));}
TMP inline ccf Min(ccf a,ccf b,ccf c){return Min(a,Min(b,c));}
TMP inline ccf READ(ccf* _arr,int _n){RP(t,1,_n)_arr[t]=qr((ccf)1);}
//----------------------template&IO---------------------------
int seg[maxn*81];
int data[maxn*81];
int sL[maxn*81];
int sR[maxn*81];
int rt[maxn];
int cnt;
int n,m;
void build0(int l,int r,int pos){
    if(l==r) {data[pos]=qr(1);return;}
    sL[pos]=++cnt;sR[pos]=++cnt;midd;
    build0(lef);build0(rgt);
}

void build(int last,int k,int l,int r,int pos){
    if(l==r)  {data[pos]=qr(1);return;}midd;
    if(k<=mid){sL[pos]=++cnt;sR[pos]=sR[last];build(sL[last],k,lef);}
    else      {sR[pos]=++cnt;sL[pos]=sL[last];build(sR[last],k,rgt);}
}

void upd(int last,int k,int l,int r,int pos){
    if(l==r)  {printf("%d\n",data[pos]=data[last]);return;}midd;
    if(k<=mid){sL[pos]=++cnt;sR[pos]=sR[last];upd(sL[last],k,lef);}
    else      {sR[pos]=++cnt;sL[pos]=sL[last];upd(sR[last],k,rgt);}
}

int main(){
#ifndef ONLINE_JUDGE
    freopen("in.in","r",stdin);
    freopen("out.out","w",stdout);
#endif
    n=qr(1);m=qr(1);
    rt[0]=cnt=1;
    build0(1,n,1);
    for(register int t=1,t1,t2;t<=m;++t){
	t1=qr(1);t2=qr(1);rt[t]=++cnt;
	if(t2==1) build(rt[t1],qr(1),1,n,rt[t]);
	else upd(rt[t1],qr(1),1,n,rt[t]);
    }
    return 0;
}